對偶原理：

有兩個定理（或命題），如果一個定理中的所有元素和運算替換為對應的對偶元素的就成為另一個定理時，這兩個定理是相互對偶的。兩個相互對偶的定理，如果其中一個定理真實，則另一個必然真實。數學上可以證明它的正確性。

所以“對偶“在數學中，指某些成對的概念，從它們本身的含義看是很不相同的。但從某種抽象規律或性質去看，不僅是一一對應的而且可以說是完全一致。如果能夠根據某種規律或性質，證得成對概念中一個具有性質A，那麽另一概念也必須具有性質A的原則。

從上可知對偶式相互的；對偶是一種廣義對稱。對稱是數學美的重要特征之一。因此，對偶原理從方法論的角度來講，便是數學的美學方法的一個具體體現，而且這一美學方法又與真緊密聯系在一起，因此，它的作用也就顯得更加重要了。

關於對偶原理的註意點

1．對偶命題是相互的。

2．對偶與等效是兩個不同的概念，不可混淆。另外也不是相似和對稱。

對偶性是事物的基本屬性，因為任何事物往往都處於方向相反，作用不同的對立狀態之中，且雙方相互聯結、相互依賴，各方都以對方為自己存在的條件。

在數學中，某些對偶的事物，雖然本身意義不同，但其抽象的規律或性質，不僅可以一一對應，而且也可能完全一致。這樣就有可能使具有這種性質的兩對偶對象，建立起如下的結構關系體系，使在該體系中，對某一對象成立的命題，對其對偶的對象同樣成立，這時就說該體系實現了結果關系的對偶化，並說它們間建立了對偶原理。

對偶原理是個普遍的原理，適用於除涉及度量性質外的一切陳述和定理，不需要什麽中間支撐物。

平面對偶圖：

在圖論中，平面圖是可以畫在平面上並且使得不同的邊可以互不交疊的圖。

平面對偶圖一類特殊的圖。指由一個平面圖派生出的另一平面圖。

在平面圖G的每個面內選取一點作為頂點，對於G的任一條邊。，將與其相鄰的兩個面內的頂點用一條僅與‘有一交點且不與圖G的其他任何邊相交的簡單曲線連結，這樣得到的平面圖稱為G的平面對偶圖，記為G’.亦稱G’為G的幾何對偶.平面對偶具有對稱性，即，若G’為G的平面對偶圖，則G亦為G’的平面對偶圖.如圖2-12中的實線和虛線分別代表互為對偶的兩個平面圖.若圖G和G’的邊集間可建立一個一一對應，使得任何一對對應邊集E,和E;有以下關系:

其中，r’(G)和r分別為圖的上秩和秩，(E扮為邊集E1.在G

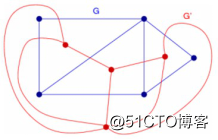
圖2-12

在軟件設計中，有很多是對偶的不同結構對象，例如：值和指針，我們先從值和地址來看，其在值上的任何操作其實在地址上進行相關的操作是對偶的，例如對值進行“+”或者“-”的操作，其對指針的操作也就是位置的偏移，其滿足的原理是對偶的。

又例如引用和對象也是對偶的，我們對某個類型所對應的對象引用的操作處理和對此對象的操作處理都是一致的，如果此引用是接口的引用，而對象是接口，那麽接口的引用和接口對象也是對偶的，這需要大家引起註意，因為接口的引用和接口對象聯合起來就形成了我們的“組合”設計（相對於繼承設計）的組成部分，這其實給了我們非常大的空間可以進行研究和分析。

通過對偶的方式，我們可以站在不同的角度來定義和分析，這就好比如射影幾何中通過對偶的點坐標和線坐標來看待射影幾何其實是一樣的，而對於置換幾何來說，也有相似的性質，例如變量和對象在通過封裝等操作情況下形成對偶，我們可以將變量看成最原始的操作，然後所有的對象都是這些成員變量的屬性構成，而站在另一個角度來說，所有的成員變量我們都可以通過封裝成一個對象來進行操作，例如我們站在前一個視角從變量來看對於一個對象A中其內部存在一個×××的變量a，如果我們從對象的角度來看，其×××的變量a，也可以看成Integer類型對應的對象a，所以這樣的不同視角可以大大擴展我們的軟件設計的領域的眼界和想象空間。

對於置換幾何來說，其內部包含很多對偶的情況，這對於我們進行深入的研究和驗證都是非常有幫助的，通過對偶我們可以在缺少信息的情況下也能夠進行合理的推廣。當然，目前對對偶的理解還不是很充分，在數學上我們還沒有找到是什麽更加深刻的原理支配對偶原理的根源。

另外從平面對偶圖也可以反過來看出，置換幾何也是存在對偶關系，而且此對偶關系能夠為我們針對復雜問題進行轉換給出一種更好的方式和方法，雖然目前的結論還較少，但是我相信這裏還存在大量的規律可供繼續深挖。

連載24：軟件體系設計新方向：數學抽象、設計模式、系統架構與方案設計(簡化版)(袁曉河著)