嶺回歸——減少過擬合問題
什麽是過擬合?
在訓練假設函數模型h時,為了讓假設函數總能很好的擬合樣本特征對應的真實值y,從而使得我們所訓練的假設函數缺乏泛化到新數據樣本能力。
怎樣解決過擬合
過擬合會在變量過多同時過少的訓練時發生,我們有兩個選擇,一是減少特征的數量,二是正則化,今天我們來重點來討論正則化,它通過設置懲罰項讓參數θ足夠小,要讓我們的代價函數足夠小,就要讓θ足夠小,由於θ是特征項前面的系數,這樣就使特征項趨近於零。嶺回歸與Lasso就是通過在代價函數後增加正則化項。
多元線性回歸損失函數:

嶺回歸回歸代價函數:

嶺回歸的原理
我們從矩陣的角度來看。機器學習的核心在在於求解出θ使J(θ)最小。怎樣找到這個θ,經典的做法是使用梯度下降通過多次叠代收斂到全局最小值,我們也可以用標準方程法直接一次性求解θ的最優值。當回歸變量X不是列滿秩時, XX‘的行列式接近於0,即接近於奇異,也就是某些列之間的線性相關性比較大時,傳統的最小二乘法就缺乏穩定性,模型的可解釋性降低。因此,為了解決這個問題,需要正則化刪除一些相關性較強特征。
標準方程法:

加上正則化後:

這裏,λ>=0是控制收縮量的復雜度參數:λ的值越大,收縮量越大,共線性的影響越來越小。在不斷增大懲罰函數系數的過程中,畫出估計參數0(λ)的變化情況,即為嶺跡。通過嶺跡的形狀來判斷我們是否要剔除掉該特征(例如:嶺跡波動很大,說明該變量參數有共線性)。
步驟:1.首先要對數據進行一些預處理,盡量把保持所有特征在一個範圍內,使用特征縮放和均值歸一化來處理特征值是很有必要的,否則,不同特征的特征值大小是沒有比較性的。
2.其次構建懲罰函數,針對不同的λ,畫出嶺跡圖。
3.根據嶺跡圖,選擇要剔除那些特征。
一個sckit-learn的example
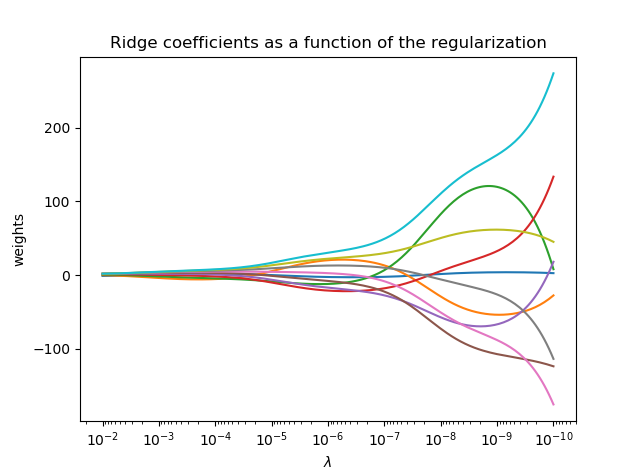
將嶺系數繪制為正則化的函數
本例顯示了共線性對估計量系數的影響。嶺回歸是本例中使用的估計量。 每種顏色表示系數矢量的不同特征,並且這是作為正則化參數的函數顯示的。這個例子還顯示了將嶺回歸應用於高度病態的基質的有用性。對於這樣的矩陣,目標變量的輕微變化會導致計算權重的巨大差異。在這種情況下,設置一定的正則化(λ)來減少這種變化(噪音)是有用的。當λ很大時,正則化效應支配平方損失函數,並且系數趨於零。在路徑的末尾,由於λ趨於零,並且解決方案傾向於普通最小二乘,所以系數顯示出大的振蕩。 在實踐中,需要調整λ以使兩者之間保持平衡。
import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model #X為一個10*10的矩陣 X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis]) y = np.ones(10) ############################################################################## #設置不同的lambda和參數 n_lambda = 200 lambda = np.logspace(-10, -2, n_lambda) coefs = [] for a in lambda: ridge = linear_model.Ridge(lambda=a, fit_intercept=False) ridge.fit(X, y) coefs.append(ridge.coef_) # ############################################################################# #顯示繪制結果 ax = plt.gca() ax.plot(lambda, coefs) ax.set_xscale(‘log‘) ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis plt.xlabel(r‘$\lambda$‘) plt.ylabel(‘weights‘) plt.title(‘Ridge coefficients as a function of the regularization‘) plt.axis(‘tight‘) plt.show()
結果:
感謝您的閱讀,如果您喜歡我的文章,歡迎關註我哦

嶺回歸——減少過擬合問題
