題目描述

棟棟有一塊長方形的地，他在地上種了一種能量植物，這種植物可以采集太陽光的能量。在這些植物采集能量後，棟棟再使用一個能量匯集機器把這些植物采集到的能量匯集到一起。

棟棟的植物種得非常整齊，一共有n列，每列有m棵，植物的橫豎間距都一樣，因此對於每一棵植物，棟棟可以用一個坐標(x, y)來表示，其中x的範圍是1至n，表示是在第x列，y的範圍是1至m，表示是在第x列的第y棵。

由於能量匯集機器較大，不便移動，棟棟將它放在了一個角上，坐標正好是(0, 0)。

能量匯集機器在匯集的過程中有一定的能量損失。如果一棵植物與能量匯集機器連接而成的線段上有k棵植物，則能 量的損失為2k + 1。例如，當能量匯集機器收集坐標為(2, 4)的植物時，由於連接線段上存在一棵植物(1, 2)，會產生3的能量損失。註意，如果一棵植物與能量匯集機器連接的線段上沒有植物，則能量損失為1。現在要計算總的能量損失。

下面給出了一個能量采集的例子，其中n = 5，m = 4，一共有20棵植物，在每棵植物上標明了能量匯集機器收集它的能量時產生的能量損失。

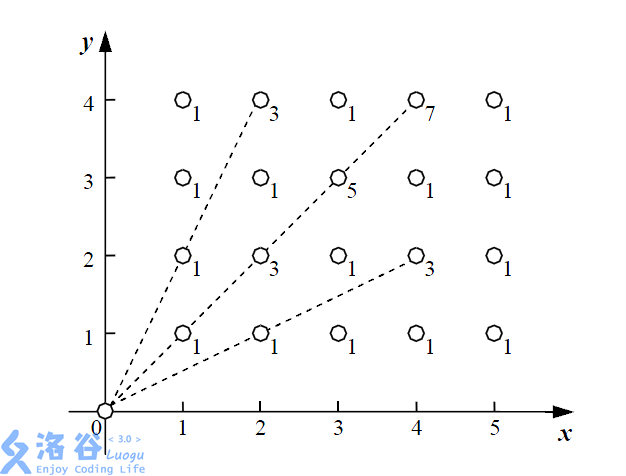
在這個例子中，總共產生了36的能量損失。

輸入輸出格式

輸入格式：

僅包含一行，為兩個整數n和m。

輸出格式：

僅包含一個整數，表示總共產生的能量損失。

輸入輸出樣例

5 4

36

3 4

20

說明

對於10%的數據：1 ≤ n, m ≤ 10；
對於50%的數據：1 ≤ n, m ≤ 100；
對於80%的數據：1 ≤ n, m ≤ 1000；
對於90%的數據：1 ≤ n, m ≤ 10,000；
對於100%的數據：1 ≤ n, m ≤ 100,000。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int gcd(int x,int y)
{
    return !y?x:gcd(y,x%y);
}

int n, m, ans;
int main()
{
    scanf("%d %d",&n, &m);
    for(int i = 1; i <= n; ++ i)
    {
        for(int
 
 j = 1; j <=m; ++ j)
        {
            ans += 2 * gcd(i, j) - 1;
        }
    }
    printf("%d", ans);
    return 0;
}

//Pro:P1447 [NOI2010]能量采集

//首先要思考的問題就是(x,y)與(0,0)之間有多少個點？ 
//顯然(x,y)在(t*x,t*y)的前面
//所以(x,y)前面一定也會有(t*X,t*Y)
//如果gcd(X,Y)=1，那麽t=gcd(x,y)
//所以(x,y)前面一共gcd(x,y)個點(包括(x,y))
//那麽就可以得到一個暴力算法：
//for(int i = 1; i <= n; ++ i)
//    {
//        for(int j = 1; j <=m; ++ j)
//        {
//            ans += 2 * gcd(i, j) - 1;
//        }
//    } 
//這樣80分T兩個點

//所以現在我們要改進這個做法
//一個點一個點地去枚舉是O(n*m)的，這顯然不太明智
//那麽我們考慮去枚舉(x,y)的gcd g
//可以知道n裏有n/g個數的因子裏有g，m裏有m/g個 
//這些數隨機組合成坐標，一共有(n/g)*(m/g)種
//但是這是以g為公因子的，不是以g為最大公因子的
//所以我們要把那些以g的倍數為最大公因子的篩掉（容斥）
//開一個數組f[i]記錄以i為gcd的坐標的個數 
//那麽f[i]=(n/g)*(m/g)-f[i的倍數]
//然後讓ans+=f[i]*(i*2-1) 

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

const int N=1e5+5;

int n,m;
long long f[N],ans;
int main()
{
    scanf("%d%d",&n,&m);
    if(n>m)
        swap(n,m);
    for(int i=n;i;--i)
    {
        f[i]=(1ll*n/i)*(m/i);
        for(int j=2;j*i<=n;++j)
            f[i]-=f[i*j];
        ans+=f[i]*1ll*(i*2-1);
    }
    printf("%lld",ans);
    return 0;
}

P1447 [NOI2010]能量采集