數據結構(12)_樹的概念及通用樹的實現
1.1.樹的相關定義
1.樹的定義
樹是一種非線性的數據結構,右n(n>=0)個結點組成的有限集合,如果n=0,稱為空樹,如果n>0,則:
- 有一個特定的結點被稱之為跟結點(root),根結點只有直接後繼,沒有前驅,
-
除根結點外的其他結點劃分為m(m>=0)個互不相交的有限集合T0,T1...Tm-1,每一個集合又是一顆子樹,並稱之為跟的子樹。
樹的示例如下: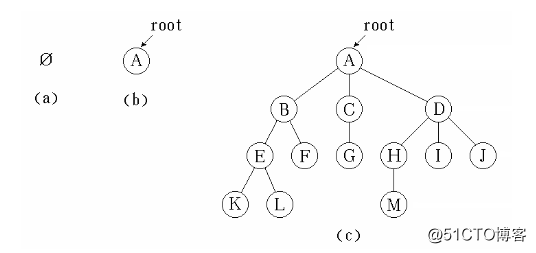
2.樹中度的概念
樹的結點包含一個數據及如果指向子樹的分支,結點擁有的子樹數目稱為結點的度(度為0的結點稱為葉結點;度不為0稱為分支結點);
樹的度定義為所有結點中度的最大值。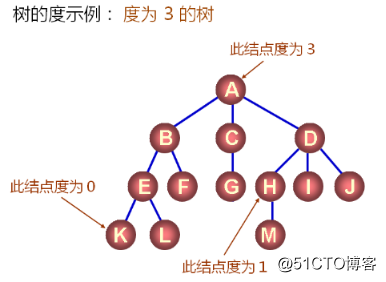
3.樹的前驅和後繼
結點的直接後繼稱為該結點的孩子,相應的,該結點稱為孩子的雙親;
結點的孩子的孩子,稱為該結點的子孫,相應 該結點稱為子孫的祖先;
同一個雙親的孩子之間互稱兄弟。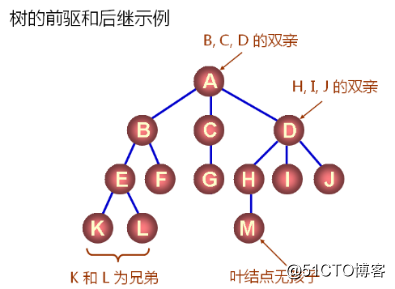
4.樹中結點的層次
樹中結點最大層次稱為樹的深度或高度。
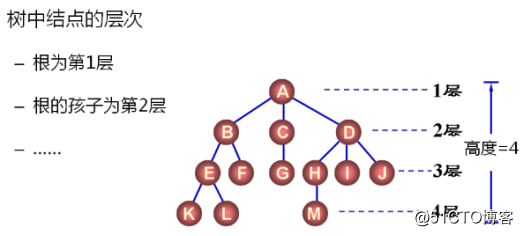
5.樹的有序性
如果樹中結點的各個子樹從左向右是有次序的,子樹間不能互換位置,則稱該樹為有序樹,否則為無序樹。

6.森林的概念
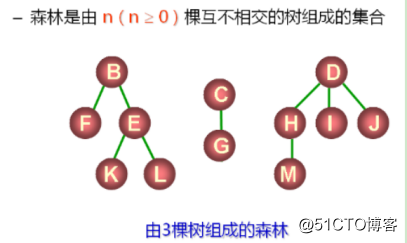
1.2.樹的抽象定義
與其他的數據結構一樣,樹的常用操作包括:插入、刪除、查找(獲取樹的節點)、獲取樹的高度/深度、獲取樹的度、清空樹中的元素等。
1.2.1.樹的抽象定義
template < typename T > class Tree : public Object { protected: TreeNode<T>* m_root; public: Tree() { m_root = NULL; } virtual bool insert(TreeNode<T>* node) = 0; virtual bool insert(const T& value, TreeNode<T>* node) = 0; virtual SharedPointer<Tree<T>> remove(TreeNode<T>* node) = 0; virtual SharedPointer<Tree<T>> remove(const T& value) = 0; virtual TreeNode<T>* find(TreeNode<T>* node) const = 0; virtual TreeNode<T>* find(const T& value) const = 0; virtual TreeNode<T>* root() const = 0; virtual int degree() const = 0; virtual int hight() const = 0; virtual int count() const = 0; virtual void clear() =0; };1..2.2.樹的節點的抽象定義
樹的節點也表現為一種特殊的數據類型
template < typename T > class TreeNode : public Object { public: TreeNode<T>* m_parent; TreeNode() { m_parent = NULL; } virtual ~TreeNode() = 0; };樹與節點的類關系:都繼承自頂層父類Object,通過樹的節點與樹形成組合關系。
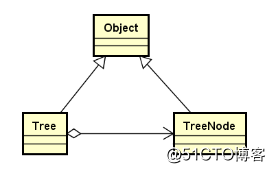
總結: - 樹是一種非線性的數據結構,擁有唯一前驅(父節點)和若幹後繼(子節點);
- 樹的結點包含一個數據及若幹指向其他節點的指針,在程序中表現為一種特殊的數據類型。
2.樹的存儲結構設計
課程目標:完成樹和結點的存儲結構設計。
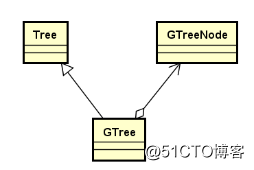
前面我們實現了樹的抽象結構,本節我們實現一個通用樹結構的基本框架。類繼承結構如下圖所示: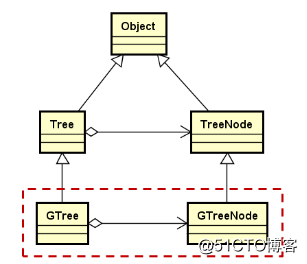
設計要點:
1.GTree為通用樹結構,每個結點可以存在多個後繼結點;
2.GTreeNode能夠包含任意多指向後繼結點的指針
3.實現樹結構的所有操作(增、刪、查、改、等)2.1.GTreeNode的設計與實現
我們使用單鏈表組合完成GTreeNode的實現,便於在GTreeNode中存儲多個指向其後繼結點的指針;
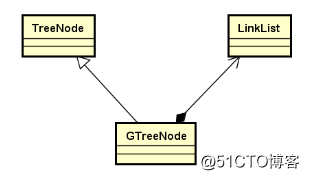
template < typename T > class GTreeNode : public TreeNode<T> { public: LinkList<GTreeNode<T>*> child; ~GTreeNode(){} };2.2.GTree的設計與實現
template<typename T> class GTree : public Tree<T> { };2.3.GTree(通用樹結構)的架構實現
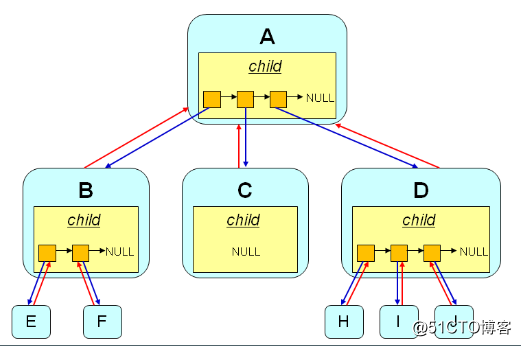
問題:每個樹結中為什麽要包含指向前驅結點的指針?
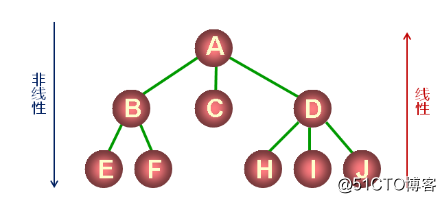
3. 樹的通用操作實現
3.1.樹中結點的查找操作
查找方式:
- 基於數據元素值的查找
GTreeNode<T>* find(const T& value) const -
基於結點的查找
GTreeNode<T>* find(TreeNode<T>* node) const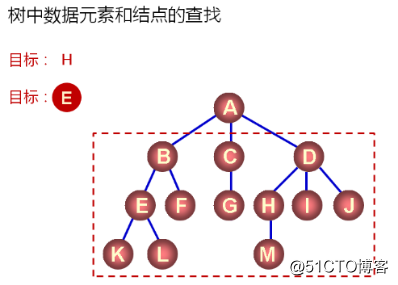
基於數據元素值的查找:
定義功能函數:find (node, value),在node為根結點的樹中遞歸查找value所在的節點
GTreeNode<T>* find(GTreeNode<T>* node, const T& value)const { GTreeNode<T>* ret = NULL; if(node != NULL) { //如果根結點的就是目標結點 if(node->value == value) { ret = node; } else { //遍歷根節點的子結點 for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next()) { //對每個子子結點進行查找 ret = find(node->m_children.current(), value); } } } return ret; } //查找結點 virtual GTreeNode<T>* find(const T& value)const { return find(root(), value); }基於結點的查找:
定義功能函數:find(node, obj),在node為根結點的樹中遞歸查找是否存在obj結點;
GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj)const { GTreeNode<T>* ret = NULL; //根結點為目標結點 if(node == obj) { ret = node; } else { if(node != NULL) { //遍歷子結點 for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next()) { ret = find(node->m_children.current(), obj); } } } return ret; } virtual GTreeNode<T>* find(TreeNode<T>* node)const { return find(root(), dynamic_cast<GTreeNode<T>*>(node)); }總結:
1.查找操作是樹的關鍵操作之一,插入函刪除操作都依賴於查找操作;
2.基於數據元素的查找可以判斷值是否存在於樹中;基於結點的查找可以判斷樹中是否存在指定結點;3.1.樹中結點的插入操作
插入方式:
- 插入新的結點
bool insert(TreeNode<T>* node) - 插入新的數據元素
bool insert(const T& value,TreeNode<T>* parent)
問題:如何指定新結點在樹中的位置?
1.樹是非線性的,無法采用下標的形式定位數據元素
2.每一個樹結點都有一個唯一的前驅結點(父節點),必須先找到前驅結點才能完成結點的插入;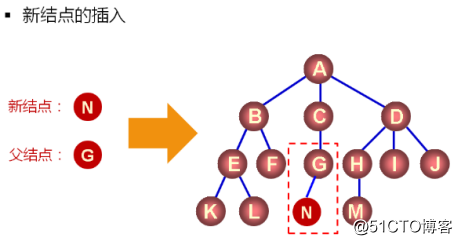
插入節點操作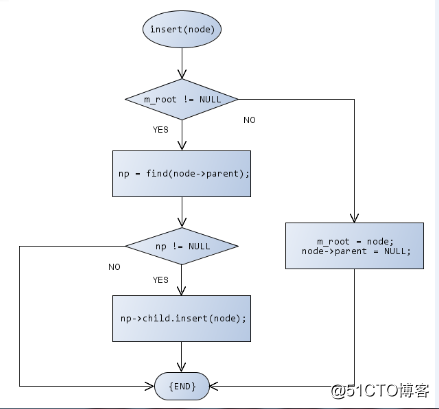
bool insert(TreeNode<T>* node) { bool ret = true; if(node != NULL) { //樹為空,插入結點為根結點 if(this->m_root == NULL) { node->parent = NULL; this->m_root = node; } else { //找到插入結點的父結點 GTreeNode<T>* np = find(node->parent); if(np != NULL) { GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node); //如果子結點中無該結點,插入結點 if(np->m_children.find(n) < 0) { ret = np->m_children.insert(n); } } else { THROW_EXCEPTION(InvalidOperationException, "Invalid node..."); } } } else { THROW_EXCEPTION(InvalidParameterException, "Parameter is invalid..."); } return ret; }插入數據元素:
bool insert(const T& value, TreeNode<T>* parent) { bool ret = true; GTreeNode<T>* node = GTreeNode<T>::NewNode(); if(node != NULL) { node->value = value; node->parent = parent; insert(node); } else { THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory..."); } return ret; }總結:
1.插入操作是構建樹的唯一操作,需要從堆空間中創建結點
2.執行插入操作必須正確處理指向父節點的指針
3.3.樹中結點的清除操作
3.3.1.清除操作
清除操作的定義:void clear() //將樹中的所有節點清除(釋放堆中的節點)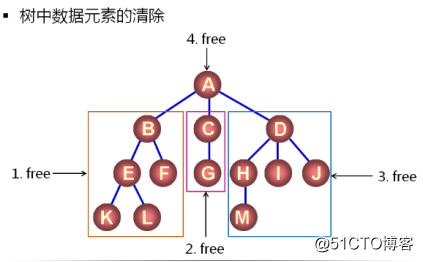
清除操作功能函數定義:
free(node) //清除node為根結點的樹,釋放樹中的每一個結點
問題:樹中的結點可能來源於不同的存儲空間,如何判斷堆空間中的結點並釋放?
1.單憑內存地址很難準確判斷具體的存儲區域;
2.只有堆空間的內存才需要主動釋放(delete)
3.清除操作時只需要對堆中的結點進行釋放
3.3.2.工廠模式
1.在GTreeNode中增加保護成員m_flag;
2.將GTreeNode中的operator new重載為保護成員函數;
3.提供工廠方法GTreeNode<T>* NewNode()
4.在工廠方法中new新結點並將m_flage設置為true;
樹結點的工廠模式示例:
template <typename T>
class GTreeNode:public TreeNode<T>
{
protected:
bool m_flag;//堆空間標識
//重載new操作符,聲明為保護
void* operator new(unsigned int size)throw()
{
return Object::operator new(size);
}
public:
LinkedList<GTreeNode<T>*> m_children;
GTreeNode()
{
//棧上分配的空間標識為false
m_flag = false;
}
//工廠方法,創建堆空間的結點
static GTreeNode<T>* NewNode()
{
GTreeNode<T>* ret = new GTreeNode<T>();
if(ret != NULL)
{
//堆空間的結點標識為true
ret->m_flag = true;
}
return ret;
}
//堆空間結點標識訪問函數
bool flag()const
{
return m_flag;
}
};
//結點的釋放:
void free(GTreeNode<T>* node)
{
if(node != NULL)
{
for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
{
free(node->m_children.current());
}
//如果結點存儲在堆空間
if(node->flag())
delete node;//釋放
}
}
//清空樹:
void clear()
{
free(root());
this->m_root = NULL;
}總結:
1.清除操作用於銷毀樹中的每個結點,需要釋放對應的內存空間;
2.工廠模式可用於“定制”堆空間中的結點,只有銷毀定制結點的時候需要進行釋放
3.4樹中結點的刪除操作
刪除的方式:
- 基於數據元素的刪除
SharedPointer< Tree<T> > remove(const T& value) -
基於結點的刪除
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
刪除操作成員函數的操作要點:
1.被刪除的結點所代表的子樹進行刪除;
2.刪除函數返回一棵樹堆空間中的樹
3.具體返回值為指向樹的智能指針對象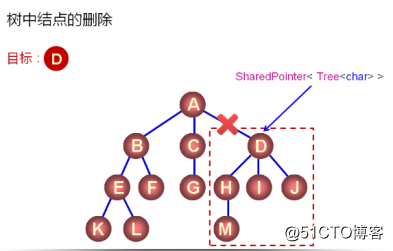
實用的設計原則:
當需要從函數中返回堆中的對象時,使用智能指針(SharedPointer)作為函數的返回值。
刪除操作功能函數定義:void remove(GTreeNode<T>* node, GTree<T>*& ret)
1.將node為根結點的子樹從原來的樹中刪除
2.Ret做為子樹返回(ret指向堆空間中的樹對象)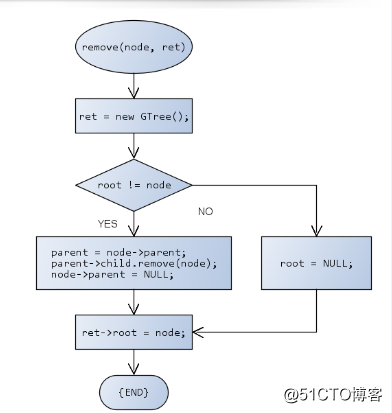
template <typename T> class GTreeNode:public TreeNode<T> { protected: bool m_flag;//堆空間標識 //重載new操作符,聲明為保護 void* operator new(unsigned int size)throw() { return Object::operator new(size); } public: LinkedList<GTreeNode<T>*> m_children; GTreeNode() { //棧上分配的空間標識為false m_flag = false; } //工廠方法,創建堆空間的結點 static GTreeNode<T>* NewNode() { GTreeNode<T>* ret = new GTreeNode<T>(); if(ret != NULL) { //堆空間的結點標識為true ret->m_flag = true; } return ret; } //堆空間結點標識訪問函數 bool flag()const { return m_flag; } }; 結點的釋放: void free(GTreeNode<T>* node) { if(node != NULL) { for(node->m_children.move(0); !node->m_children.end(); node->m_children.next()) { free(node->m_children.current()); } //如果結點存儲在堆空間 if(node->flag()) delete node;//釋放 } } 清空樹: void clear() { free(root()); this->m_root = NULL; }總結:
1.刪除操作將目標節點所代表的子樹移除,返回值為指向樹智能指針對象;
2.刪除操作必須完善處理父節點和子節點的關系;
3.函數中返回堆中的對象時,使用智能指針作為返回值。3.5.樹的屬性操作實現
3.5.1.樹中結點的數目
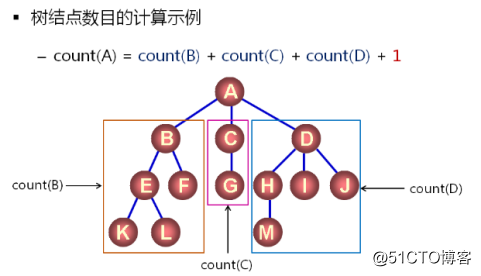
定義功能,count(node),在node為根結點的樹中統計結點數目。
使用遞歸實現:結點數目 = 子樹結點數目+1(根結點)。
int count(GTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
ret = 1;//根結點
//遍歷根節點的子結點
for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
{
ret += count(node->m_children.current());
}
}
return ret;
}
//樹的結點數目訪問函數
int count()const
{
count(root());
}3.5.2.樹的高度
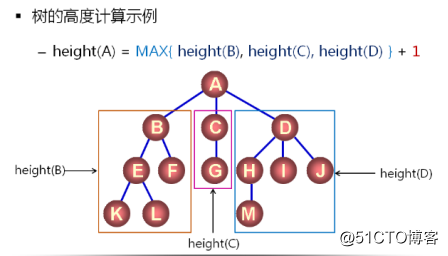
功能定義:height(node),獲取node為根結點的樹的高度。
遞歸實現:樹的高度 = 子樹結點高度的最大值 + 1(根結點)。
int degree(GTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
//結點的子結點的數量
ret = node->m_children.length();
//遍歷子結點
for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
{
int d = degree(node->m_children.current());
if(ret < d)
{
ret = d;
}
}
}
return ret;
}
//樹的度訪問函數
int degree()const
{
return degree(root());
}3.5.3.樹的度數
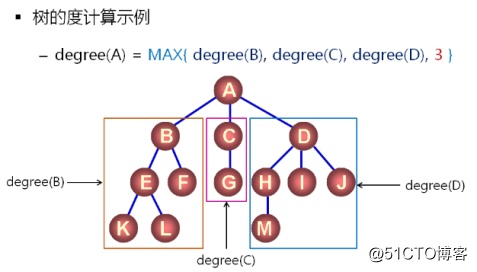
功能定義:degree(node),獲取node為結點的樹的度數。
遞歸實現:樹的度數 = 子樹的最大度數 + 1(根結點)
int height(GTreeNode<T>* node)const
{
int ret = 0;
if(node != NULL)
{
//遍歷子結點
for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
{
//當前結點的高度
int h = height(node->m_children.current());
if(ret < h)
{
ret = h;
}
}
ret = ret + 1;
}
return ret;
}
//樹的高度訪問函數
int height()const
{
height(root());
}3.6.樹形結構的層次遍歷
問題:如何按照層次遍歷通用樹結構中的每一個數據元素?
當前的事實:- 樹是一種非線性的數據結構,樹的節點沒有固定的編號方式;
新的需求:- 為通用樹結構提供新的方法,快速遍歷每一個節點
設計思路:
在樹中定義一個新遊標(GTreeNode<T>*),遍歷開始將遊標指向根結點(root()),獲取遊標指向的數據元素,通過結點中的child成員移動遊標;
提供一組遍歷相關的函數,按層次訪問樹中的數據元素。
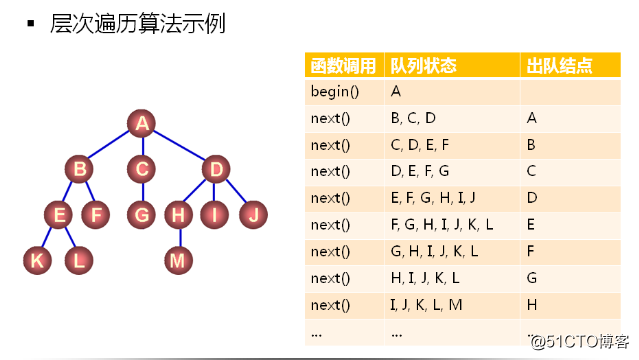
層次遍歷算法:
原料:class LinkQueue<T>; 遊標:LinkQueue<T>::front();
思想:
- begin() 將根結點壓人隊列中
- current() 訪問隊頭指向的數據元素
- next() 隊頭元素彈出,將隊頭元素的孩子壓入隊列中(核心)
-
end() 判斷隊列是否為空
//將根結點壓入隊列中 bool begin() { bool ret = (root() != NULL); if(ret) { //清空隊列 m_queue.clear(); //根節點加入隊列 m_queue.add(root()); } return ret; } //判斷隊列是否為空 bool end() { return (m_queue.length() == 0); } //隊頭元素彈出,將隊頭元素的孩子壓入隊列中 bool next() { bool ret = (m_queue.length() > 0); if(ret) { GTreeNode<T>* node = m_queue.front(); m_queue.remove();//隊頭元素出隊 //將隊頭元素的子結點入隊 for(node->m_children.move(0); !node->m_children.end(); node->m_children.next()) { m_queue.add(node->m_children.current()); } } return ret; } //訪問隊頭元素指向的數據元素 T current() { if(!end()) { return m_queue.front()->value; } else { THROW_EXCEPTION(InvalidOperationException, "No value at current Node..."); } }總結:
1.樹的結點沒有固定的編號方式,可以按照層次關系堆樹中的結點進行遍歷;
2.通過遊標的思想設計成員函數,遍歷函數是相互依賴,相互配合的;
3.遍歷操作的核心是隊列的使用。4. 通用樹的最終實現
4.1 GTree的實現
template<typename T> class GTree : public Tree<T> { protected: LinkQueue<GTreeNode<T>*> m_queue; GTree(const GTree<T>&); GTree<T>& operator =(const GTree<T>&); //容器的內容不能復制 GTreeNode<T>* find(GTreeNode<T>* node, const T& value) const { GTreeNode<T>* ret = NULL; if(node != NULL) { if(node->value == value) { ret = node; } else { // 遍歷單鏈表(樹中子結點的指針), for(node->child.move(0); (!node->child.end()) && (ret==NULL); node->child.next()) { ret = find(node->child.current(), value); } } } return ret; } GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj) const { GTreeNode<T>* ret = NULL; if(node != NULL) { if(node == obj) { ret = node; } else { for(node->child.move(0);!node->child.end() && (ret == NULL);node->child.next()) { ret = find(node->child.current(),obj); } } } return ret; } //清空數的功能函數,遞歸是釋放每個子樹 void free(GTreeNode<T>* node) { if(node != NULL) //遞歸出口 { for(node->child.move(0); !node->child.end(); node->child.next()) { free(node->child.current()); } //如果結點存在於堆空間,則釋放 if(node->flag()) { delete node; } /*else { cout << node->value << endl; }*/ } } // 刪除操作的功能函數,(1.將node為根結點的子樹從原來的樹中刪除 2.Ret做為子樹返回(ret指向堆空間中的樹對象)) void remove(GTreeNode<T>* node, GTree<T>*& ret) //ret 是一個指針的別名 { ret = new GTree(); if(ret != NULL) { if(node == root()) { this->m_root = NULL; } else { //獲取刪除結點的父結點的子結點鏈表 LinkList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->m_parent)->child; // 從鏈表中刪除節點 child.remove(child.find(node)); // 結點的父結點置NULL node->m_parent = NULL; } // 將刪除結點賦值給創建的樹ret的根結點 ret->m_root = node; } else { THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create GTree..."); } } int count(GTreeNode<T>* node) const { int ret = 0; if(node != NULL) { ret = 1; //根結點 //遞歸計算子樹的節點 for(node->child.move(0); !node->child.end(); node->child.next()) { ret += count(node->child.current()); } } return ret; } int height(GTreeNode<T>* node) const { int ret = 0; if(node != NULL) { for(node->child.move(0); !node->child.end(); node->child.next()) { int h = height(node->child.current()); if(h > ret) //獲取子樹高度的最大值 { ret = h; } } ret = ret + 1/*根結點*/; } return ret; } int degree(GTreeNode<T>* node) const { int ret = 0; if(node != NULL) { ret = node->child.length(); for(node->child.move(0); !node->child.end(); node->child.next()) { int d = degree(node->child.current()); if(ret < d) { ret = d; //獲取子樹高度的最大度數 } } } return ret; } public: GTree(){} bool insert(TreeNode<T>* node) { bool ret = true; if(node != NULL) { if(this->m_root == NULL) { this->m_root = node; node->m_parent = NULL; } else { GTreeNode<T>* np = find(node->m_parent); if(np != NULL) { GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node); // 防止重復插入 if( np->child.find(n) < 0 ) { np->child.insert(n); } } else { THROW_EXCEPTION(InvaildParemeterException, "can‘t find parent node for current node..."); } } } else { THROW_EXCEPTION(InvaildParemeterException, "con‘t insert NULL node..."); } return ret; } bool insert(const T& value, TreeNode<T>* parent) { bool ret = true; GTreeNode<T>* node = GTreeNode<T>::NewNode(); if(node != NULL) { node->value = value; node->m_parent = parent; insert(node); } else { THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create node... "); } return ret; } SharedPointer< Tree<T> > remove(const T& value) { GTree<T>* ret = NULL; GTreeNode<T>* node = find(value); if(node != NULL) { remove(node, ret); m_queue.clear(); m_queue.clear(); } else { THROW_EXCEPTION(InvaildParemeterException, "invaild paremeter..."); } return ret; } SharedPointer< Tree<T> > remove(TreeNode<T>* node) { GTree<T>* ret = NULL; node = find(node); if(node != NULL) { remove(dynamic_cast<GTreeNode<T>*>(node), ret); } else { THROW_EXCEPTION(InvaildParemeterException, "invaild paremeter..."); } return ret; } GTreeNode<T>* find(const T& value) const { return find(root(),value); } GTreeNode<T>* find(TreeNode<T>* node) const { return find(root(), dynamic_cast<GTreeNode<T>*>(node)); } GTreeNode<T>* root() const { return dynamic_cast<GTreeNode<T>*>(this->m_root); } int degree() const { return degree(root()); } int count() const { return count(root()); } int height() const { return height(root()); } void clear() { free(root()); this->m_root = NULL; } bool begin() { bool ret = (root() != NULL); if(ret) { m_queue.clear(); m_queue.enqueue(root()); } return ret; } bool end() { return (m_queue.length() == 0); } bool next() { bool ret = (m_queue.length() > 0); if(ret) { GTreeNode<T>* node = m_queue.front(); m_queue.dequeue(); for(node->child.move(0); !node->child.end(); node->child.next()) { m_queue.enqueue(node->child.current()); } } return ret; } T current() { if(!end()) { return m_queue.front()->value; } else { THROW_EXCEPTION(InvalidOperationException, "invalid operation ..."); } } ~GTree() { clear(); m_queue.clear(); } };
4.2. GTreeNode的實現
template < typename T >
class GTreeNode : public TreeNode<T>
{
protected:
//堆空間標識,如果在堆空間中創建了結點,則置為true,以便後續釋放結點時判斷結點是否創建自堆空間
bool m_flag;
GTreeNode(const GTreeNode<T>&);
GTreeNode<T>& operator =(const GTreeNode<T>&); //容器的內容不能復制
//重載new操作符,聲明為保護成員
void* operator new(unsigned int size)throw()
{
return Object::operator new(size);
}
public:
LinkList<GTreeNode<T>*> child;
GTreeNode()
{
m_flag = false;
}
static GTreeNode<T>* NewNode()
{
GTreeNode<T>* ret = new GTreeNode<T>();
if(ret != NULL)
{
ret->m_flag = true; //在堆空間中申請了結點,則將該標識置為true
}
return ret;
}
//堆空間結點標識訪問函數
bool flag()const
{
return m_flag;
}
~GTreeNode(){}
};
數據結構(12)_樹的概念及通用樹的實現
