二分法適用於求單調的時候用的，就比如說排序好的數組，那是遞增的或者遞減的。如果像出現了非單調函數那樣的怎麽求它的最值呢？

二分法早就失去了他的意義了。不過還是可以用三分法來實現的，就是二分中再來二分。三分查找的算法，對於求凸性或凹性函數的極值非常方便

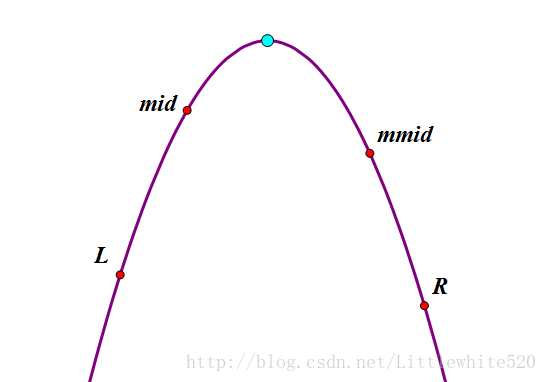
如圖所示，已知左右端點L、R，要求找到極值點的位置。
思路：通過不斷縮小 [L,R] 的範圍，無限逼近極值點。
做法：先取 [L,R] 的中點 mid，再取 [mid,R] 的中點 mmid，通過比較 f(mid) 與 f(mmid) 的大小來縮小範圍。
當最後 L=R-1 時，再比較下這兩個點的值，我們就找到了答案。
1、當 f(mid) > f(mmid) 的時候，我們可以斷定 mmid 一定在極值點的右邊。

反證法：假設 mmid 在極值點的左邊，則 mid 也一定在極值點的左邊，又由 f(mid) > f(mmid) 可推出 mmid < mid，與已知矛盾，故假設不成立。

所以，此時可以將 R = mmid 來縮小範圍。
2、當 f(mid) < f(mmid) 的時候，我們可以斷定 mid 一定在極值點的左邊。

反證法：假設 mid 在極值點的右邊，則 mmid 也一定在極值點的右邊，又由 f(mid) < f(mmid) 可推出 mid > mmid，與已知矛盾，故假設不成立。

同理，此時可以將 L = mid 來縮小範圍。

摘自https://blog.csdn.net/littlewhite520/article/details/70144763

第一種寫法

 1 double  solve(double l,double r)
 2 {
 3     double mid,midmid;
 4     while(r - l > eps)
 5     {
 6         mid = (l + r)/2.0;
 7         midmid = (r + mid)/2.0;
 8         if(f(mid) <= f(midmid))// f 就算函數值
 9             r = midmid;
10         else  l = mid;
11     }
12
 
     return f(l);
13 }

第二種寫法

 1 double three_devide(double low,double up)  
 2 {  
 3     double m1,m2;  
 4     while(up-low>=eps)  
 5     {  
 6         m1=low+(up-low)/3;  
 7         m2=up-(up-low)/3;  
 8         if(f(m1)<=f(m2))  
 9             low=m1;  
10         else  
11             up=m2;  
12     }  
13     return (m1+m2)/2;  
14 }  

Light Bulb

Compared to wildleopard‘s wealthiness, his brother mildleopard is rather poor. His house is narrow and he has only one light bulb in his house. Every night, he is wandering in his incommodious house, thinking of how to earn more money. One day, he found that the length of his shadow was changing from time to time while walking between the light bulb and the wall of his house. A sudden thought ran through his mind and he wanted to know the maximum length of his shadow.

Input

The first line of the input contains an integer T (T <= 100), indicating the number of cases.Each test case contains three real numbers H, h and D in one line. H is the height of the light bulb while h is the height of mildleopard. D is distance between the light bulb and the wall. All numbers are in range from 10^-2 to 10³, both inclusive, and H - h >= 10^-2.

Output

For each test case, output the maximum length of mildleopard‘s shadow in one line, accurate up to three decimal places..

Sample Input

3

2 1 0.5

2 0.5 3

4 3 4

Sample Output

1.000

0.750

4.000

三分法搜索