數據結構(一)-----4種方法求最大子列和
阿新 • • 發佈:2018-07-23
include iss 需要 中間 () log 完整 font sso
數據結構(一)-----4種方法求最大子列和
1、暴力算法
/* 作者:mys 功能:求最大子列和 日期:2018/7/23 */ #include<stdio.h> #include<stdlib.h> #define N 1000 int maxSubseSum(int a[], int n); void main() { int a[N] = { 0 },i; for (i = 0; i < N; i++) a[i] = rand() % 10000; printf("maxSubseSum=%d\n", maxSubseSum(a, N)); system("pause"); } int maxSubseSum(int a[],int n) { int thisSum, maxSum = 0; int i, j, k; for (i = 0; i < n; i++)//i是子列左端位置 { for (j = i; j < n; j++)//j是子列右端位置 { thisSum = 0;//thisSum:a[i]到a[j]的子列和 for (k = i; k <= j; k++) { thisSum += a[k]; if (thisSum>maxSum)//更新結果 maxSum = thisSum; } } } return maxSum; }
因為有3重for循環,因此時間復雜度為:T(N)=O(N^3),時間復雜度太大,不理想,下面是稍微優化後的。
2、稍微優化
#include<stdio.h> #include<stdlib.h> #define N 1000 int maxSubseSum(int a[], int n); void main() { int a[N] = { 0 }, i; for (i = 0; i < N; i++) a[i] = rand() % 10000; printf("maxSubseSum=%d\n", maxSubseSum(a, N)); system("pause"); } int maxSubseSum(int a[], int n) { int thisSum, maxSum = 0; int i, j; for (i = 0; i < n; i++)//i是子列左端位置 { thisSum = 0;//thisSum:a[i]到a[j]的子列和 for (j = i; j < n; j++)//j是子列右端位置 { thisSum += a[j]; if (thisSum>maxSum)//更新結果 maxSum = thisSum; } } return maxSum; }
T(N)=O(N^2)
時間復雜度稍微好一點,但還是比較大,程序員一般看到時間復雜度是N^2,就會想辦法將其復雜度變為NlogN,因此出現了下面的分而治之法。
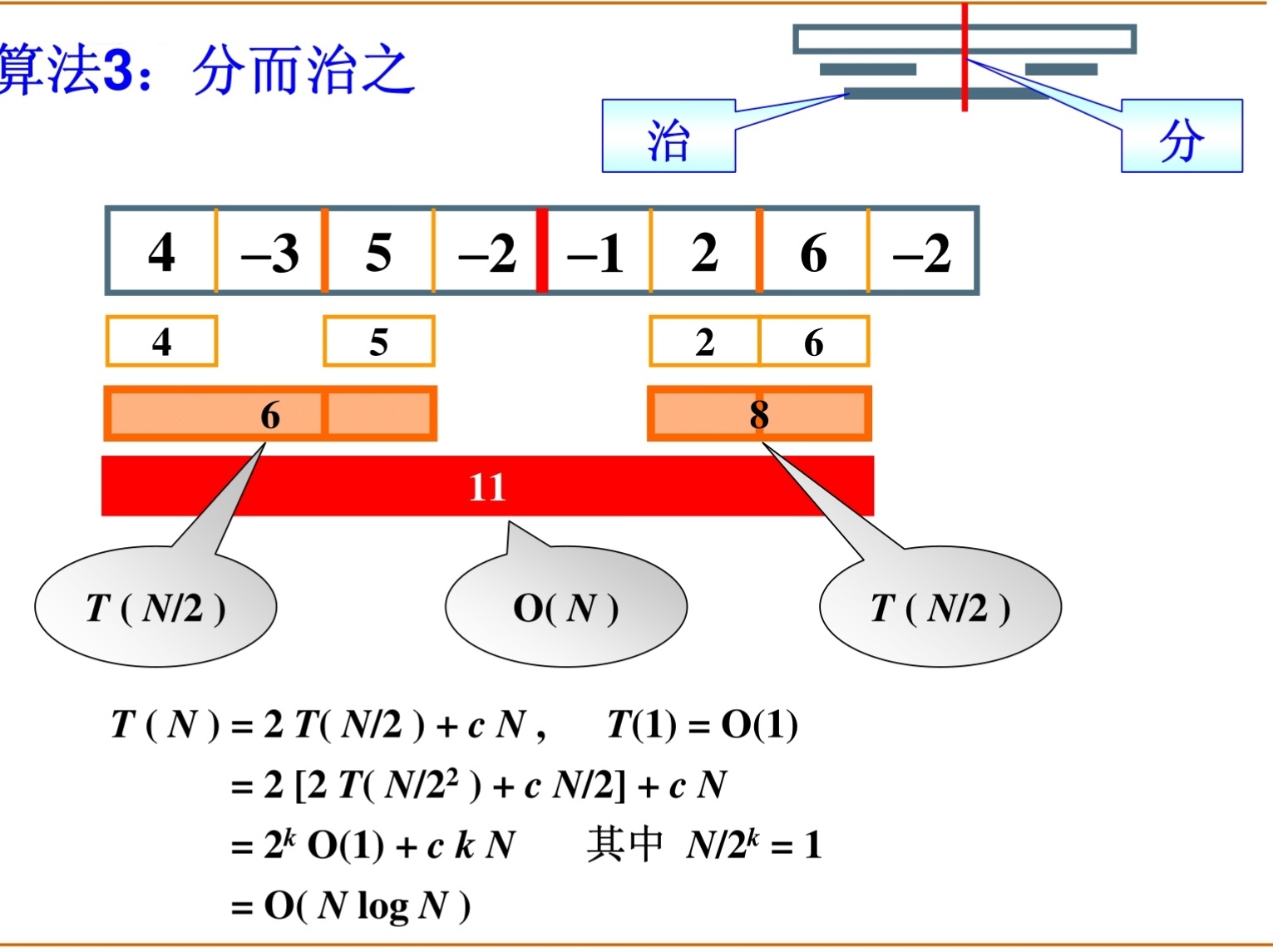
3、分而治之
/* 作者:mys 功能:求最大子列和(分而治之) */ #include<stdio.h> #include<stdlib.h> #define N 1000 //求三個數的最大值 int Max(int a, int b, int c) { int max; max = (a > b) ? a : b; max = (max > c) ? max : c; return max; } //遍歷整個子列求最大值 int maxCross(int a[], int left, int mid, int right) { int leftSum=0,rightSum=0,sum=0; int i; //遍歷從中間到左邊 for (i = mid; i >=left; i--) { sum += a[i]; if (sum > leftSum) leftSum = sum; } //遍歷從中間到右邊 sum = 0; for (i = mid + 1; i <= right; i++) { sum += a[i]; if (sum > rightSum) rightSum = sum; } return leftSum + rightSum; } //分而治之 int divideAndRule(int a[], int left,int right) { int mid=0; int maxLeft=0, maxRight=0, maxMiddle=0; //如果只有一個數 if (left == right) { if (a[left] > 0) return a[left]; else return 0; } //求中間值 mid = (left + right) / 2; //對左邊的子列用分而治之法 maxLeft = divideAndRule(a, left, mid); //對右邊的子列用分而治之法 maxRight = divideAndRule(a, mid + 1, right); //遍歷整個子列 maxMiddle = maxCross(a,left,mid,right); return Max(maxLeft, maxRight, maxMiddle); } void main() { int a[N] = { 0 }, i; for (i = 0; i < N; i++) a[i] = rand() % 10000; printf("divideAndRule=%d\n", divideAndRule(a, 0, N - 1)); system("pause"); }
此程序的時間復雜度計算如下:
T(N)為程序的整個遞歸的時間復雜度,因此前半的時間復雜度為T(N/2);不斷替換,直到T(1);其中N/2^k=1是因為N不斷除2,約為k次,因此k=logN 註:復雜度分析小竅門
這個時間復雜度為NlogN,還算比較優化,但還不是最優的方法,下面這個在線處理方法算是最優化的,時間復雜度T(N)=O(N),就算遍歷完整個子列也需要O(N),因此這個算法是最優化的了。
4、在線處理
/*
作者:mys
功能:求最大子列和(在線處理)
*/
#include<stdio.h>
#include<stdlib.h>
#define N 1000
void main()
{
int a[N] = { 0 }, i;
for (i = 0; i < N; i++)
a[i] = rand() % 10000;
printf("onlineProcess=%d\n", onlineProcess(a,N));
system("pause");
}
int onlineProcess(int a[], int n)
{
int sum = 0, maxSum = 0;
int i;
for (i = 0; i < n; i++)
{
sum += a[i];//向右累加
if (sum>maxSum)
maxSum = sum;//更新結果
else if (sum < 0)//如果當前子列和為負,則不可能使後面部分的值增大,因此舍去
maxSum = 0;
}
return maxSum;
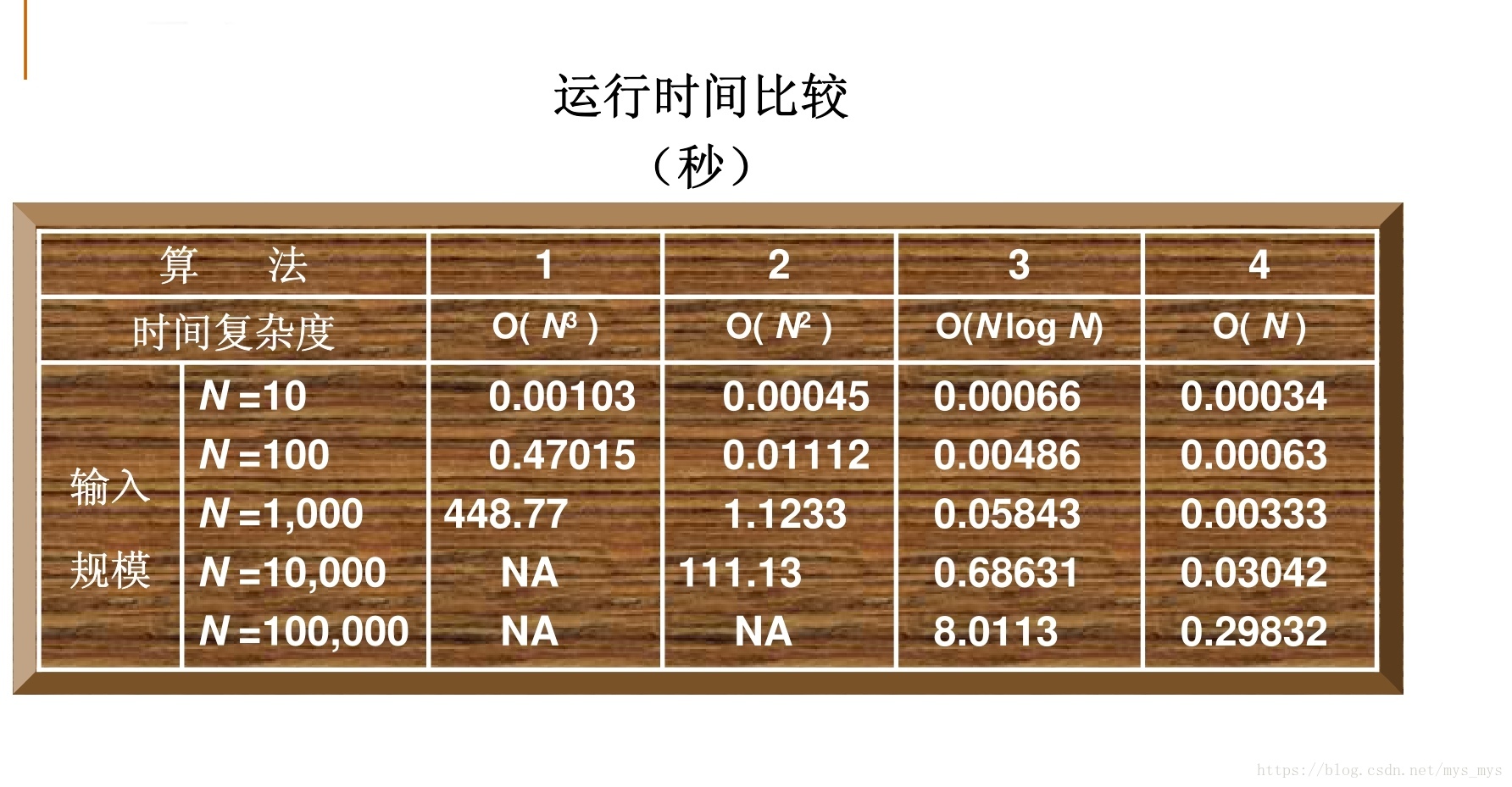
}下圖是這四個算法的運行時間比較
NA表示not avaliable,從上可看出分而治之O(NlogN)和在線處理O(N) 算法還是比較好。
----------------------------------------------------------------------------------2018.7.23以上是我今天整理的數據結構的一點小小的筆記,以後還會繼續更新^-^
數據結構(一)-----4種方法求最大子列和