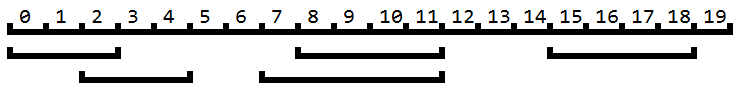
上圖一共有5個區間，分別是[0,2]、[2,4]、[8,11]、[7,11]、[15,18]。如果要求這些區間合並後區間的大小，有兩種簡單的方法。

　　方法一：比較每兩個區間的範圍，如果兩個區間有交集，則合並它們。最後所有區間會合並成幾個離散的大區間，結果為這些區間大小之和。這種方法的時間復雜度是O(n^2)。

　　方法二：使用一個可以覆蓋所有區間範圍的數組，對每個區間進行標記，結果為數組中被標記元素的個數。這種方法的時間復雜度是O(nm)。

　　註：n是區間個數，m是所有區間總的範圍。

　　如果n和m都比較大，那麽上述兩種方法的效率都不高。這裏有一種很巧妙的解決這個問題的方法，它的時間復雜度是O(n+m)。使用一個可以覆蓋所有區間範圍的數組flg，初始化時將數組中的元素都置為0。對於每一個區間[l,r]，將flg[l]++，flg[r+1]--。最後使用一個累加器cnt，初始置為0。依次掃描數組中的每一個元素，對於第i個元素，cnt+=flg[i]。此時，若cnt>0，則說明i在某些區間中；若cnt==0，則證明i不在任何區間中。統計cnt>0的元素個數即可。

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <string>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <cmath>
#include <list>
#include <deque>
#include <map>
#include 
 
<set>
using namespace std;
#define ll long long
const double PI = acos(-1.0);
const int maxn = 101;
const int INF = 0x3f3f3f3f;
int dx[]={0,0,-1,1};
int dy[]={-1,1,0,0};

int n,m;
int f[maxn],cnt=0,sum=0;
struct node
{
    int l,r;
}a[maxn];
int main()
{
    scanf("%d%d",&n,&m);
    
 
for(int i=0;i<n;i++)
    {
        scanf("%d %d",&a[i].l,&a[i].r);
    }
    for(int i=0;i<n;i++)
    {
        f[a[i].l]++;
        f[a[i].r+1]--;
    }
    for(int i=0;i<m;i++)
    {
        sum+=f[i];
        if(sum>0)
            cnt++;
    }
    printf("%d\n",cnt);
}

求多個區間合並後區間大小的巧妙解決方法【差分】