題目描述

菲菲和牛牛在一塊n 行m 列的棋盤上下棋，菲菲執黑棋先手，牛牛執白棋後手。 棋局開始時，棋盤上沒有任何棋子，兩人輪流在格子上落子，直到填滿棋盤時結束。

落子的規則是：一個格子可以落子當且僅當這個格子內沒有棋子且這個格子的左側及上方的所有格子內都有棋子。

棋盤的每個格子上，都寫有兩個非負整數，從上到下第i 行中從左到右第j 列的格 子上的兩個整數記作Ai,jA_{i,j}Ai,j? 、Bi,jB_{i,j}Bi,j? 。在遊戲結束後，菲菲和牛牛會分別計算自己的得分：菲菲的得分是所有有黑棋的格子上的Ai,jA_{i,j}Ai,j? 之和，牛牛的得分是所有有白棋的格子上的Bi,jB_{i,j}Bi,j?的和。

菲菲和牛牛都希望，自己的得分減去對方的得分得到的結果最大。現在他們想知道，在給定的棋盤上，如果雙方都采用最優策略且知道對方會采用最優策略，那麽，最終的結果如何。

輸入輸出格式

從文件chess.in 中讀入數據。

輸入第一行包含兩個正整數n;m，保證n;m <= 10。

接下來n 行，每行m 個非負整數，按從上到下從左到右的順序描述每個格子上的 第一個非負整數：其中第i 行中第j 個數表示Ai,jA_{i,j}Ai,j?。

接下來n 行，每行m 個非負整數，按從上到下從左到右的順序描述每個格子上的 第二個非負整數：其中第i 行中第j 個數表示Bi,jB_{i,j}Bi,j?。

輸出到文件chess.out 中。

輸出一個整數，表示菲菲的得分減去牛牛的得分的結果。

輸入輸出樣例

2 3
2 7 3
9 1 2
3 7 2
2 3 1

2

說明

樣例1說明：

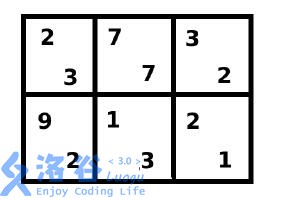
棋盤如圖所示，雙方都采用最優策略時，棋局如下：

• 菲菲下在第1 行第1 列（這是第一步時唯一可以落子的格子）；

• 牛牛下在第1 行第2 列；

• 菲菲下在第2 行第1 列；

• 牛牛下在第1 行第3 列；

• 菲菲下在第2 行第2 列；

• 牛牛下在第2 行第3 列（這是這一步時唯一可以落子的格子）；

• 填滿棋盤，遊戲結束，盤面如下。

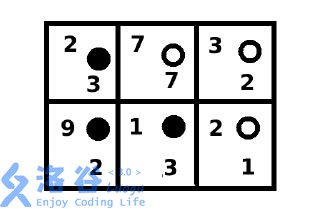
菲菲的得分為：2 + 9 + 1 = 12 ；牛牛的得分為：7 + 2 + 1 = 10 。

對於所有的測試數據，n;m <= 10 ，Ai,jA_{i,j}Ai,j?; Bi,jB_{i,j}Bi,j? <= 100000。

對於編號為奇數的測試點，保證所有的Bi,jB_{i,j}Bi,j? = 0 。

省選時被吊打的畫面歷歷在目...

註意到它一定是一個階梯狀的狀態，所以我們hash記錄一下每一行填到的位置。

設f[i]表示hash值為i的狀態之後的先手減後手的最大值/最小值，因為一個狀態唯一確定一個接下來操作的人，所以實現上不用管它最大還是最小。

顯然先手要獲得$\large max(f[s‘] + a[i][j])$， 後手要獲得$\large min(f[s‘] - b[i][j])$.

於是min-max對抗搜索。

但是狀態量極大數組開不下，考慮到有用的狀態不多，所以用map存儲。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
#define reg register
#define int long long
inline int read() {
    int res=0;char ch=getchar();bool fu=0;
    while(!isdigit(ch)) {if(ch==‘-‘)fu=1;ch=getchar();}
    while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
    return fu?-res:res;
}
#define base 12
int n, m; 
int a[15][15], b[15][15];
int jie[15];
int END;
inline int hash() {
    int res = 0;
    for (reg int i = 0 ; i <= n ; i ++) 
        res = res * base + jie[i];
    return res;
}

map <int, int> f;
int ans;

int dfs(int opt, int sit) 
{
    if (f.find(sit) != f.end()) return f[sit];
    int tmp = sit;
    for (reg int i = n ; i >= 1 ; i --) jie[i] = tmp % base, tmp /= base;
    if (!opt) { //the first person 
        int res = -1e9;
        for (reg int i = 1 ; i <= n ; i ++)
        {
            if (jie[i] == m) continue;
            if (jie[i] < jie[i-1]) {
                jie[i]++;
                int sum = a[i][jie[i]] + dfs(opt ^ 1, hash());
                res = max(res, sum);
                jie[i]--;
            }
        }
        return f[sit] = res;
    } else {
        int res = 1e9;
        for (reg int i = 1 ; i <= n ; i ++)
        {
            if (jie[i] == m) continue;
            if (jie[i] < jie[i-1]) {
                jie[i]++;
                int sum = dfs(opt ^ 1, hash()) - b[i][jie[i]];
                res = min(res, sum);
                jie[i]--;
            }
        }
        return f[sit] = res;        
    }
}

signed main()
{
    n = read(), m = read();
    for (reg int i = 1 ; i <= n ; i ++)
        for (reg int j = 1 ; j <= m ; j ++)
            a[i][j] = read();
    for (reg int i = 1 ; i <= n ; i ++)
        for (reg int j = 1 ; j <= m ; j ++)
            b[i][j] = read();
    jie[0] = m + 1;
    for (reg int i = 1 ; i <= n ; i ++) jie[i] = m;
    int END = hash();
    f[END] = 0;
    cout << dfs(0, 0) << endl;
    return 0;
}

[九省聯考2018]一雙木棋chess