【題目描述】

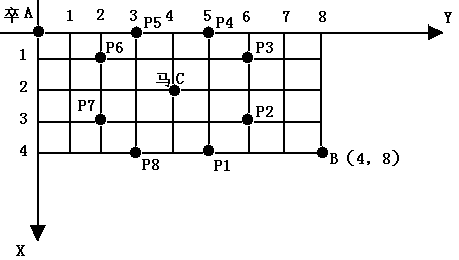
棋盤上A點有一個過河卒，需要走到目標B點。卒行走的規則：可以向下、或者向右。同時在棋盤上的某一點有一個對方的馬（如C點），該馬所在的點和所有跳躍一步可達的點稱為對方馬的控制點，如圖3-1中的C點和P1，……，P8，卒不能通過對方馬的控制點。棋盤用坐標表示，A點(0,0)、B點(n, m) (n,m為不超過20的整數),同樣馬的位置坐標是需要給出的，C≠A且C≠B。現在要求你計算出卒從A點能夠到達B點的路徑的條數。

【輸入】

給出n、m和C點的坐標。

【輸出】

從A點能夠到達B點的路徑的條數。

【輸入樣例】

8 6 0 4

【輸出樣例】

1617

【來源】

Noip2002

這個題是一道經典的老題一直都想寫一下，終於在一個伸手不見五指的夜晚如願以償，用時2個小時，調試時間過長，主要原因是腦子反應過慢。這個題有個很麻煩的地方是故意把坐標給混亂，想了半天終於有一種好的辦法，就是將原圖向左翻轉90度。如下圖：

這樣就不會混亂，坐標軸就與給定坐標對應。這個題的遞推邊界一定要考慮好，而且馬的控制點這一塊一定要細心，不然很容易出錯。

 1 #include<iostream>
 2 using namespace std;
 3 int n, m, cx, cy;
 4 long long f[40][40], g[40][40];//註意盡量使用long long不然容易超出數據範圍 
 5 int main()
 6 {
 7     cin>>n>>m>>cx>>cy;
 8     f[0][0]=1;
 9     //以下考慮馬的控制點有無越界 
 

10     g[cx][cy]=1;
11     if(cx-1>=0&&cy-2>=0)g[cx-1][cy-2]=1;
12     if(cx+1<=n&&cy-2>=0)g[cx+1][cy-2]=1;
13     if(cx-2>=0&&cy-1>=0)g[cx-2][cy-1]=1;
14     if(cx+2<=n&&cy-1>=0)g[cx+2][cy-1]=1;
15     if(cx-2>=0&&cy+1<=m)g[cx-2][cy+1]=1
 
;
16     if(cx+2<=n&&cy+1<=m)g[cx+2][cy+1]=1;
17     if(cx-1>=0&&cy+2<=m)g[cx-1][cy+2]=1;
18     if(cx+1<=n&&cy+2<=m)g[cx+1][cy+2]=1;
19     
20     //以下為遞推邊界 
21     for(int i=1; i<=n; i++)
22         if(!g[i][0])f[i][0]=f[i-1][0];
23     for(int j=1; j<=m; j++)
24         if(!g[0][j])f[0][j]=f[0][j-1];
25     //以下為遞推關系式，相對簡單能想到    
26     for(int i=1; i<=n; i++)
27         for(int j=1; j<=m; j++)
28         {
29             if(g[i][j])f[i][j]=0;
30             if(!g[i][j])f[i][j]=f[i][j-1]+f[i-1][j];
31         }
32 //調試代碼所用
33 //    for(int i=0; i<=n; i++)
34 //    {
35 //        for(int j=0; j<=m; j++)cout<<f[i][j]<<" ";
36 //        cout<<endl;
37 //    }
38     cout<<f[n][m];
39     return 0;
40 }

另外這個題應該可以用到搜索，等講到搜索用搜索寫第二種方法，所以本篇文章未完待續。。。。。。

【例3.6】過河卒(Noip2002)