NOI 2017 D1T1 壓位 線段樹
$ \Rightarrow $ 戳我進洛谷原題 $ \Rightarrow $ 戳我進BZOJ原題
[Noi2017]整數
時空限制 $ \quad $ 2000ms / 512MB
題目背景
在人類智慧的山巔,有著一臺字長為 $ 1048576 $ 位(此數字與解題無關)的超級計算機,
著名理論計算機科學家P博士正用它進行各種研究。不幸的是,這天臺風切斷了電力系統,
超級計算機無法工作,而 P 博士明天就要交實驗結果了,只好求助於學過OI的你. . . . . .
題目描述
P 博士將他的計算任務抽象為對一個整數的操作。具體來說,有一個整數 $ x $ ,一開始為 $ 0 $ 。
接下來有 $ n $ 個操作,每個操作都是以下兩種類型中的一種:
1 a b :將 $ x $ 加上整數 $ a\cdot 2^b $ ,其中 $ a $ 為一個整數,$ b $ 為一個非負整數
2 k :詢問 $ x $ 在用二進制表示時,位權為 $ 2^k $ 的位的值(即這一位上的 $ 1 $ 代表 $ 2^k $ )
保證在任何時候,$ x \geqslant 0 $ 。
輸入輸出格式
輸入格式:
輸入的第一行包含四個正整數 $ n,t_1,t_2,t_3 $ ,$ n $ 的含義見題目描述, $ t_1,t_2,t_3 $ 的具體含義見子任務。
接下來 $ n $ 行,每行給出一個操作,具體格式和含義見題目描述。
同一行輸入的相鄰兩個元素之間,用恰好一個空格隔開。
輸出格式:
對於每個詢問操作,輸出一行,表示該詢問的答案( $ 0 $ 或 $ 1 $ )。對於加法操作,沒有任何輸出。
輸入輸出樣例
輸入樣例
10 3 1 2
1 100 0
1 2333 0
1 -233 0
2 5
2 7
2 15
1 5 15
2 15
1 -1 12
2 15輸出樣例
0
1
0
1
0
說明
在所有測試點中,$ 1\leqslant t_1 \leqslant 3, 1 \leqslant t_2 \leqslant 4, 1 \leqslant t_3 \leqslant 2 $ 。不同的 $ t_1,t_2,t_3 $ 對應的特殊限制如下:
- 對於 $ t_1 = 1 $ 的測試點,滿足 $ a = 1 $
- 對於 $ t_1 = 2 $ 的測試點,滿足 $ |a| = 1 $
- 對於 $ t_1 = 3 $ 的測試點,滿足 $ |a| \leqslant 10^9 $
- 對於 $ t_2 = 1 $ 的測試點,滿足 $ 0 \leqslant b, k \leqslant 30 $
- 對於 $ t_2 = 2 $ 的測試點,滿足 $ 0 \leqslant b, k \leqslant 100 $
- 對於 $ t_2 = 3 $ 的測試點,滿足 $ 0 \leqslant b, k \leqslant n $
- 對於 $ t_2 = 4 $ 的測試點,滿足 $ 0 \leqslant b, k \leqslant 30n $
- 對於 $ t_3 = 1 $ 的測試點,保證所有詢問操作都在所有修改操作之後
- 對於 $ t_3 = 2 $ 的測試點,不保證詢問操作和修改操作的先後順序
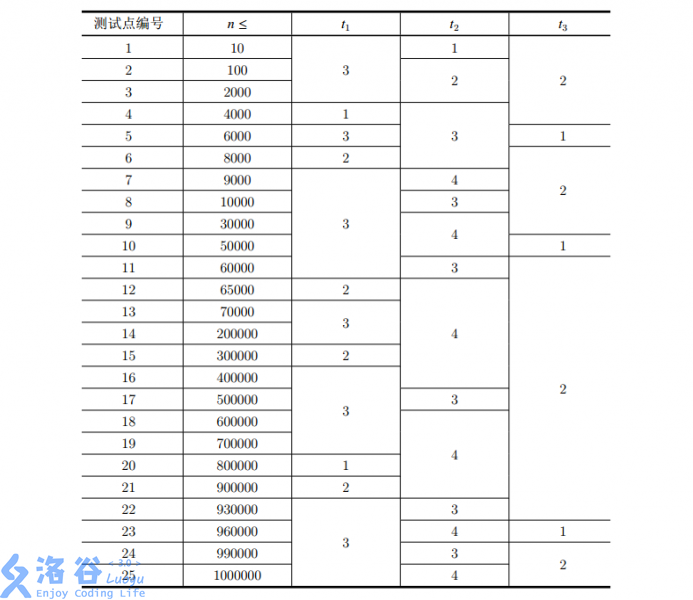
本題共 25 個測試點,每個測試點 4 分。各個測試點的數據範圍如下:
思路
本題需要用到線段樹+壓位。
首先考慮在某一位加1或減1的情況。
在加1時,我們要從當前位開始,找到最低的為0的位,然後把這一位加1,路上經過的所有位都清零。
在減1時,我們要從當前位開始,找到最低的為1的位,然後把這一位減1,路上經過的所有位都修改成1。
這些操作顯然可以在線段樹上完成。但是我們發現,操作的數位的範圍可能特別大,達到 $ 3 \times 10^7 $ , $ O(n \times log_n ) $ 的時間復雜度並不能承受。
那麽我們可以把30個二進制位壓成一位,或者甚至把60個二進制位壓成一位,
然後在操作的時候,原來的找0就變成了找第一個全不是1的段,原來的找1就變成了找第一個全不是0的段,
那麽壓位後一次修改最多涉及兩次操作,常數大大降低,就可以通過此題了。
代碼
/**************************************************************
Problem: 4942
User: PotremZ
Language: C++
Result: Accepted
Time:23424 ms
Memory:48168 kb
****************************************************************/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 1000005
const int INF=(1<<30)-1;
int n,sor[N<<2],sad[N<<2],lzy[N<<2];
inline void pushdown(int o){
sor[o<<1]=sor[o<<1|1]=sad[o<<1]=sad[o<<1|1]=lzy[o<<1]=lzy[o<<1|1]=lzy[o];
lzy[o]=-1;
}
void fix(int o,int l,int r,int pos,int val){
if(l==r){
sor[o]+=val;
sad[o]+=val;
return;
}
if(lzy[o]!=-1) pushdown(o);
int mid=l+r>>1;
if(pos>mid) fix(o<<1|1,mid+1,r,pos,val);
else fix(o<<1,l,mid,pos,val);
sor[o]=sor[o<<1]|sor[o<<1|1];
sad[o]=sad[o<<1]&sad[o<<1|1];
}
void updata(int o,int l,int r,int L,int R,int val){
if(L<=l&&r<=R){
sor[o]=sad[o]=lzy[o]=val;
return;
}
if(lzy[o]!=-1) pushdown(o);
int mid=l+r>>1;
if(L>mid) updata(o<<1|1,mid+1,r,L,R,val);
else if(R<=mid) updata(o<<1,l,mid,L,R,val);
else {
updata(o<<1,l,mid,L,R,val);
updata(o<<1|1,mid+1,r,L,R,val);
}
sor[o]=sor[o<<1]|sor[o<<1|1];
sad[o]=sad[o<<1]&sad[o<<1|1];
}
int find0(int o,int l,int r,int pos){
if(!sor[o]) return -1;
if(l==r) return l;
if(lzy[o]!=-1) pushdown(o);
int mid=l+r>>1;
if(pos>mid) return find0(o<<1|1,mid+1,r,pos);
else {
int tmp=find0(o<<1,l,mid,pos);
return tmp!=-1 ? tmp : find0(o<<1|1,mid+1,r,pos);
}
}
int find1(int o,int l,int r,int pos){
if(sad[o]==INF) return -1;
if(l==r) return l;
if(lzy[o]!=-1) pushdown(o);
int mid=l+r>>1;
if(pos>mid) return find1(o<<1|1,mid+1,r,pos);
else {
int tmp=find1(o<<1,l,mid,pos);
return tmp!=-1 ? tmp : find1(o<<1|1,mid+1,r,pos);
}
}
int query(int o,int l,int r,int pos){
if(l==r) return sad[o];
if(lzy[o]!=-1) pushdown(o);
int mid=l+r>>1;
if(pos>mid) return query(o<<1|1,mid+1,r,pos);
else return query(o<<1,l,mid,pos);
}
inline void add(int pos,int x){
int tmp=query(1,0,N,pos);
if(tmp+x<=INF) fix(1,0,N,pos,x);
else {
fix(1,0,N,pos,x-INF-1);
int ntp=find1(1,0,N,pos+1);
if(ntp!=pos+1) updata(1,0,N,pos+1,ntp-1,0);
fix(1,0,N,ntp,1);
}
}
inline void del(int pos,int x){
int tmp=query(1,0,N,pos);
if(tmp-x>=0) fix(1,0,N,pos,-x);
else {
fix(1,0,N,pos,INF+1-x);
int ntp=find0(1,0,N,pos+1);
if(ntp!=pos+1) updata(1,0,N,pos+1,ntp-1,INF);
fix(1,0,N,ntp,-1);
}
}
int main(){
scanf("%d",&n); int t1,t2,t3; scanf("%d %d %d",&t1,&t2,&t3);
while(n--){
int opt; scanf("%d",&opt);
if(opt==1){
int a,b,pos; scanf("%d %d",&a,&b); pos=b/30;
if(a==0) continue;
if(a>0){
add(pos,(a<<(b-pos*30))&INF);
add(pos+1,a>>(30-(b-pos*30)));
} else {
a=-a;
del(pos,(a<<(b-pos*30))&INF);
del(pos+1,a>>(30-(b-pos*30)));
}
} else {
int k,pos; scanf("%d",&k); pos=k/30;
printf("%c\n",(query(1,0,N,pos)&(1<<(k-pos*30)) ? 1 : 0)^'0');
}
}
return 0;
}NOI 2017 D1T1 壓位 線段樹
