這位 .net 合並 算法介紹 我們 n-1 以及 記錄 span

轉https://www.cnblogs.com/litthorse/p/9332370.html

作為(曾)被認為兩大最好的監督分類算法之一的adaboost元算法(另一個為前幾節介紹過的SVM算法)，該算法以其簡單的思想解決復雜的分類問題，可謂是一種簡單而強大的算法，本節主要簡單介紹adaboost元算法，並以實例看看其效果如何。

該算法簡單在於adaboost算法不需要什麽高深的思想，它的基礎就是一個個弱小的元結構（弱分類器），比如就是給一個閾值，大於閾值的一類，小於閾值的一類，這樣的最簡單的結構。而它的強大在於把眾多個這樣的元結構（弱分類器）組合起來一起發揮功效，所謂人多力量大，就是這個道理，組合起來的最終的分類器就是一個強分類器了。相比於SVM，SVM本身是一個個體，本身也就是一個強分類器，是一個天生的天才，而adaboost元算法，把它比如下更像是後天的天才，努力的天才，是建立在廣大人名群眾上面的天才。

好了，言歸正傳，所謂元算法，就是建立在元結構基礎上，也就是一個個弱分類器（廣大人民群眾），這個弱分類器可以任何的分類器，可以是簡單決策樹、簡單線性logistic分類器，簡單的svm等等，都可以作為它的第一層弱分類器。而一般情況下采用單層決策樹分類器作為基礎的分類器比較多。所謂單層決策樹就是給一個或者多個閾值，將一系列數分成好幾堆一樣。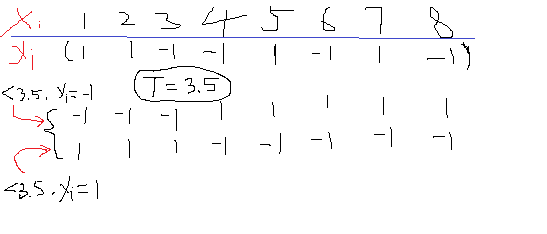

比如下面的一維數據X，其對應的標簽如下為y，那麽如果任意給定一個閾值T=3.5，那麽就可以把X分成兩類了，這裏就有個問題，小於T的是分成類1還是類-1呢？所以會存在兩種情況吧，如上面所示，至於這個閾值好不好，小於T的是歸類為1好還是-1好，那後面再說。

本節就是以這種簡單的單閾值的決策樹作為算法的元結構，也就是弱分類器來實現強分類器。好了再回來說剛剛的問題，首先你怎麽知道閾值T=3.5，答案是不知道，

那麽只能一個個取了。我找到數據X的上下限，然後設置一個步長比如10步，然後就讓T從最小值慢慢往上加吧。假設加到了T=3.5了，這個時候到了小於T是取1還是-1的時候了，所以又得分類討論如果為1，如果為-1。那麽我們怎麽去判斷閾值究竟是哪一個T好了？好了之後數據小於閾值T是是+1還是-1呢？我們看到，對於每一個閾值，然後對於該閾值下的一個取值方向（也就是小於T是+1還是-1），都會出來一個分類結果吧，有了這個結果，我把它與正確的分類結果挨個去比較看看錯誤率是多少，這樣是不是有一個評價標準了，有了這個評價標準就可以知道在遍歷所有的T的時候到底是選擇那個T最好，同時是選擇小於T的為-1還是+1的情況比較好。比如上面那個圖，在T為3.5的時候，如果小於T取-1，那麽錯了5個，所以錯誤率為5/8。如果小於T取+1，那麽正好相反錯了3個，錯誤率3/8，所以這個時候T=3.5時小於T的取+1類比較好。上面只給了T=3.5的，那麽你是不是還可以算T=4,5，等等的情況，這樣遍歷一圈後，找到那個最小錯誤率下的T以及方向是不是就知道這一組數據在這個單層決策樹下的閾值以及閾值的方向了。

那這是一維數據，如果是二維數據怎麽使用單層決策樹呢？要是二維的，那就一維一維的來吧，比如一個二維樣本點如下：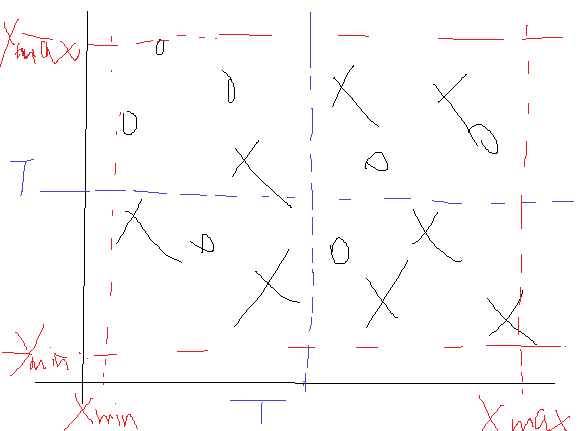

那這個時候我們先找X維的數據，也就是把所有點的x坐標提出來作為一個一維樣本，然後進行尋找最佳T與方向，方法同上面那樣，不過這個時候找到的T還多了一個標記，就是它是在哪一維上的最小誤差，比如說先找X維，那麽在X維找完後，就需要記錄三個值，一個是維度比如為1代表是在第一位上找的。一個是T，就是閾值，一個是T的方向，就是小於T的值是取+1還是-1，當然還有這一維下的最小錯誤率。完事後轉戰到第二維Y，在Y上同樣遍歷所有的T，不過這個時候遍歷的時候就要和X維找完了的那個最小錯誤率比較，也就是說如果在Y維上還能找到一個閾值T使得劃分的結果的錯誤率還小，那麽就更新這個T。所以在遍歷了所有的X維與Y維後的最優結果就需要有這麽幾個參數：一是最佳T來自於哪一維，二是這個T是多少，三是這個T下的方向是+1還是-1，四是對應下的錯誤率是多少。

那這是二維，同理可以擴展到多維吧。
好了這樣一個弱分類器（元結構）就完成了。如果單單去用這個弱分類器去分類的話顯然是不準的，這也就好比是在x或者y的某一處畫了一條直線，然後按照這條直線去分一樣。如果碰巧數據時線性的，效果會好點，碰到非線性的，效果肯定不會好的。

說了半天，我們才把一個人的力量（弱分類器）說完，我們說adaboost元算法是眾人的力量，也就是系列弱分類器的力量，那麽這一系列弱分類器是怎麽聯系起來的呢？

上面還說漏了一點內容，就是每個樣本點所占的權重問題，也就是每個樣本點在最終錯誤率上占有的比重，反之就是對正確率上占有的比重。比如上面那個二維樣本由15個樣本點，那麽我可以給相同的權重，同時為了保證所有的權重和為1，所以初始化權重D=[1/15,1/15,…….]等等15個1/15。那麽這個權重表現在哪裏呢？最後我們在算錯誤率的時候是不是需要尋找預測的與真實的類標簽差別嗎？那麽這個權重可以用在這裏，與這個差相乘。也就是如果標簽相同，差為0，對應的權重相乘完還是0，沒有用到，但是一旦不為0，那麽權重就會使得這個差按權重比例放大是不是？所以說這個權重就可以用來計算那些不一樣的點，並使得結果變得更好。

好了權重說完了，再來看看這一系列弱分類器是怎麽聯系起來的，其實聯系的方式就是改變上述權重D的過程。具體怎麽改變的呢？首先我們需要規定有多少個弱分類器，這需要自己設置。然後我們挨個的去找每個弱分類器的參數（這個參數就是上述的那幾個輸出值：屬於哪一維？T是多少？T的方向？最小誤差？當然這裏還多出一個，這個弱分類器的D是多少？）。

既然挨個的去找每個弱分類器的參數，那麽第一個弱分類器首先就假設一個D=[1/15,1/15,…….]，權重均等，有多少個樣本，每個樣本權重就是多少分之一。然後去找吧，最終會出來T及其參數吧。那麽第一個弱分類器找完了。接下來第二個弱分類器，若果D不做任何改變，是不是第二個弱分類器出來的結果T什麽的和第一個會一模一樣？對，就是一樣。那麽這個時候關鍵的地方來了，第二個弱分類器會學習第一個弱分類器，假設第一個弱分類器出來的結果，錯誤率為?,那麽

我們來分析一下，在?出來後，那麽α也就定了，並且是個大於0的數吧。那麽如果某個樣本分對了，去看看那個公式，發現其對應的權值D變小了，而如果某個樣本分錯了，其對應的D會變大的。好了對於這一次的弱分類器，一旦完成後我們就去更新它的D，並且把這個D傳遞到下一次的弱分類器構建中。我們再想想，比如說上次樣本1在上一個弱分類器中分錯了，那麽它的D就會增加吧，把麽它傳到這一次的弱分類時，在計算它產生的誤差的時候，就會因為D的增加而把使得誤差變大吧，所以這一次尋找的結果就不會是上一次尋找到T了，因為這個時候D會把第一個樣本點產生的誤差值拉大的對不對。那麽這個時候就會尋找到一個新的T及其相關參數了。用一個圖形象表示一下：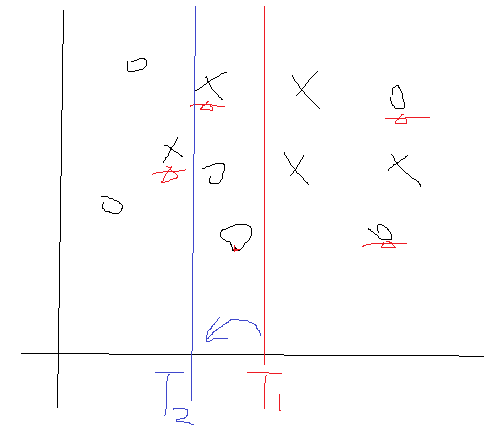

劃分錯誤的點會在下一次的劃分中被一定程度的矯正過來。

這樣第一次弱分類器就將更新後的D傳遞到第二個弱分類器的構建當中，第三個又學習第二個的弱分類器，把在第二個弱分類器中分錯的點給稍微矯正過來，這樣一直往下傳遞，弱分類器之間傳遞的唯一參數就是每個樣本的權值D。這個過程就如下所示：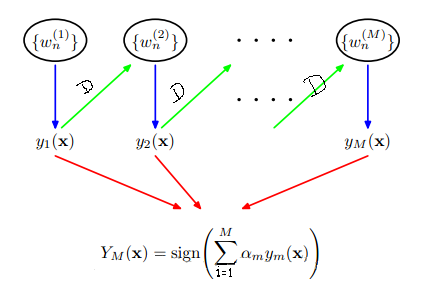

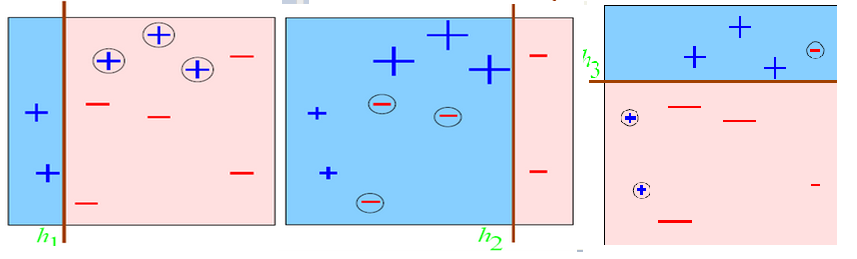
那麽這樣就可以把所有的弱分類都找出來了吧，每個弱分類器出來的結果參數（包括閾值T，T取值方向，取閾值T所屬於的原始數據維度，最小錯誤率–以及由錯誤率可以計算的α（上述公式有））是不是都可以計算出來。那麽在所有這些參數計算完了之後，怎麽區劃分原始訓練樣本以及來了的預測樣本的分類情況呢？就是上述那個公式了。每個弱分類器的α可以計算出來的，那y是什麽呢？是預測的類別，有了一個樣本，我們可以根據T屬於那個維度就可以找到這個樣本對應維度下的值了，然後看看這個值與閾值T的關系吧，看完關系後再看看是屬於+1還是-1，這就是T的方向了吧，根據這些確定這個樣本是屬於+1還是-1類，這就是y。最後把所有弱分類器的所有這樣的結果按照公式求和，把這個和取符號就是我們最終這個樣本所屬於的類了。

至此，完整的給予簡單單層決策樹的adaboost算法就到此結束了，那麽用數學符號在規整一下整個過程如下：

下面在matlab下實戰上述過程。首先還是樣本集，依然用曾經用過的非線性樣本集：

首先我們需要一個尋找一次弱分類器參數的子函數：

function [Dim,Dir,T,best_label,minError] = buildSimpleStump(data,label,D)
% 設置一個步長
numSteps = 50;
% m個樣本,每個n維
[m,n] = size(data);
thresh = 0;
minError = inf;
for i = 1:n
    min_dataI = min(data(:,i));
    max_dataI = max(data(:,i));
    step_add = (max_dataI - min_dataI)/numSteps;
    for j = 1:numSteps
        threshVal = min_dataI + j*step_add; %
        index = find(data(:,i) <= threshVal);
        %-----小於閾值的取值為-1類--------------------
        label_temp = ones(m,1);
        label_temp(index) = -1;
        index1 = find(label_temp == label);
        errArr = ones(m,1);
        errArr(index1) = 0;
        %小於閾值的誤差
        weightError = D‘*errArr;
        if weightError < minError
            bestLabel = label_temp;
            minError = weightError;
            %小於閾值的點取-1標簽
            direction = -1;
            Dim = i; %記錄屬於的維度
            thresh = threshVal;
        end      
        %-----------小於閾值的取值為+1類---------
        label_temp = -1*ones(m,1);
        label_temp(index) = 1;
        index1 = find(label_temp == label);
        errArr = ones(m,1);
        errArr(index1) = 0;
        %大於閾值的誤差
        weightError = D‘*errArr;
        if weightError < minError
            bestLabel = label_temp;
            minError = weightError;
            %小於閾值的點取+1標簽
            direction = 1;
            Dim = i; %記錄屬於的維度
            thresh = threshVal;
        end  
    end
end
Dir = direction;
T = thresh;
best_label = bestLabel;

其次需要建立所有的弱分類器：

function [dim,direction,thresh,alpha] = adaBoostTrainDs(data,label,iter)
[m,~] = size(data);
% 初始化權值D
D = ones(m,1)/m;
alpha = zeros(iter,1);
% 記錄T方向
direction = zeros(iter,1);
% 記錄T屬於哪一個維度
dim = zeros(iter,1);
% 初始化閾值T
thresh = zeros(iter,1);
for i = 1:iter
    [dim(i),direction(i),thresh(i),best_label,error] = ...
        buildSimpleStump(data,label,D);
    %計算alpha
    alpha(i) = 0.5*log((1-error)/max(error,1e-15));
    %更新權值D
    D = D.*(exp(-1*alpha(i)*(label.*best_label)));
    D = D/sum(D);
end

那麽主函數以及顯示結果如下：

clc
clear
close all
%% 加載數據
% * 最終data格式：m*n，m樣本數，n維度
% * label:m*1  標簽為-1與1這兩類
clc
clear
close all
data = load(‘data_test1.mat‘);
%選擇訓練樣本個數
num_train = 200;
%構造隨機選擇序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
label_train = train_data(:,end);
train_data = train_data(:,1:end-1);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
test_data = test_data(:,1:end-1);
predict = zeros(length(test_data),1);
%% -------訓練集訓練所有的弱分類器
iter = 50; %規定弱分類器的個數
[dim,direction,thresh,alpha] = adaBoostTrainDs(train_data,label_train,iter);
%% -------預測測試集的樣本分類
for i = 1:length(test_data)
    data_temp = test_data(i,:);
    h = zeros(iter,1);
    for j = 1:iter
        if direction(j) == -1
            if data_temp(dim(j)) <= thresh(j)
                h(j) = -1;
            else
                h(j) = 1;
            end
        elseif direction(j) == 1
            if data_temp(dim(j)) <= thresh(j)
                h(j) = 1;
            else
                h(j) = -1;
            end
        end
    end
    predict(i) = sign(alpha‘*h);
end
%% 顯示結果
figure;
index1 = find(predict==1);
data1 = (test_data(index1,:))‘;
plot(data1(1,:),data1(2,:),‘or‘);
hold on
index2 = find(predict==-1);
data2 = (test_data(index2,:))‘;
plot(data2(1,:),data2(2,:),‘*‘);
hold on
indexw = find(predict~=(label_test));
dataw = (test_data(indexw,:))‘;
plot(dataw(1,:),dataw(2,:),‘+g‘,‘LineWidth‘,3);
accuracy = length(find(predict==label_test))/length(test_data);
title([‘predict the testing data and the accuracy is :‘,num2str(accuracy)]);

某次的結果如下：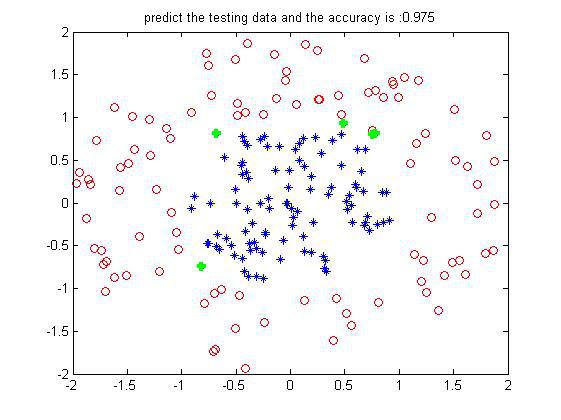

這是200個訓練樣本下200個測試樣本的預測結果（數據邊界沒有交叉的），可以看到設置的弱分類器iter為50個，每一維度步長為50，正確率還挺好。當然是不是弱分類器數目越多越好了？不一定，多了的話可能會過擬合，且到達一定程度正確率不會有太大的提升了。其實一個樣本從第一個弱分類器到最後一個弱分類器，就相對於每經過一次在上面集合切一刀一樣，最後越來越小越來越小，就屬於哪一個類了。借用網上別人的一個圖形象表示就如下：

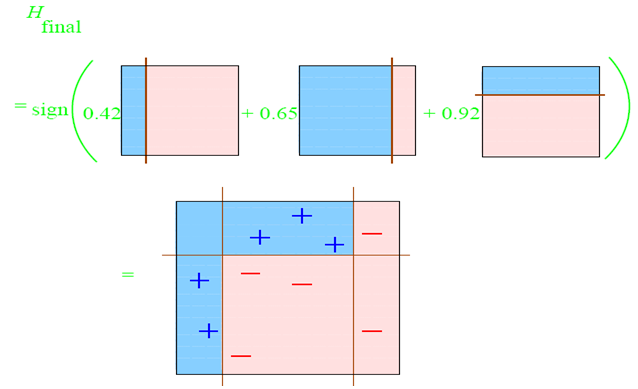
每一個弱分類器切一次：

組合起來的分類面就是：

這就是團結的力量。

----------------------------------------------------這裏是分割線-------------------------------------------------------------------------------------

上面是二分類情況，接下來是多分類：

既然是多分類樣本，首先對樣本需要理解，所謂多分類就是樣本集中不止2類樣本，至少3類才稱得上是多分類。比如下面一個二維非線性的多類樣本集（這也是後面我們實驗的樣本集）：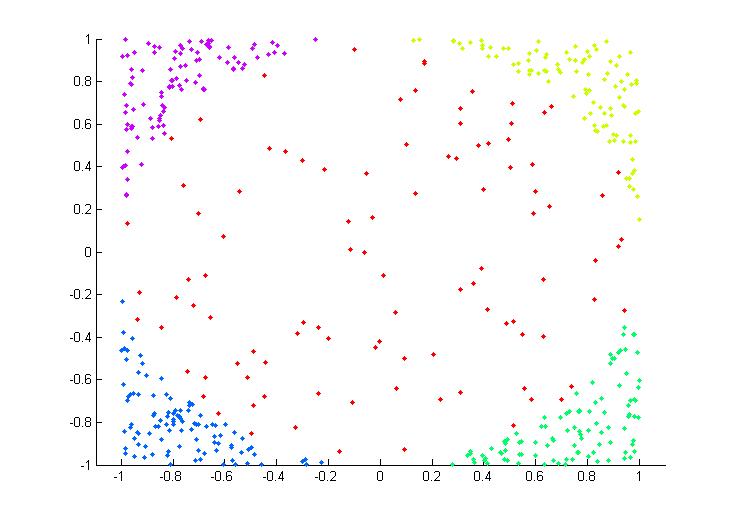

每種顏色代表一類，可以看到共有5類，同時也可以看到是一個非線性的吧，這裏可以就把五類分別設置為1~5類類標簽。

好了，曾經在單個算法介紹的時候，裏面的實驗都是二分類的（也就是只有上述5類樣本中的兩類），二分類的方式很簡單，不是你就是我的這種模式，那麽從二分類到多分類該怎麽轉換呢？假如一個樣本不是我，那也可能不是你呀，可能是他它她對吧，這個時候該如何呢？

現在一般的方式都是將多分類問題轉化為二分類問題，因為前面許多算法在原理推導上都是假設樣本是二分類的，像SVM，整個推導過程以至結論都是相對二分類的，根本沒有考慮多分類，依次你想將SVM直接應用於多分類是不可能的，除非你在從原理上去考慮多分類的情況，然後得到一個一般的公式，最後在用程序實現這樣才可以。

那麽多分類問題怎麽轉化為二分類問題？很簡單，一個簡單的思想就是分主次，采取投票機制。轉化的方式有兩種，因為分類問題最終需要訓練產生一個分類器，產生這個分類器靠的是訓練樣本，前面的二分類問題實際上就是產生了一個分類器，而多分類問題根據訓練集產生的可不止是一個分類器，而是多個分類器。

那第一種方式就是將訓練樣本集中的某一類當成一類，其他的所有類當成另外一類，像上面的5類，我把最中間的一類當成是第一類，並重新賦予類標簽為1，而把四周的四類都認為是第二類，並重新賦予類標簽維-1，好了現在的問題是不是就是二分類問題了？是的。那二分類好辦，用之前的任何一個算法處理即可。好了，這是把最中間的當成一類的情況下建立的一個分類器。同理，我們是不是也可以把四周任何一類自成一類，而把其他的統稱為一類呀？當然可以，這樣依次類推，我們共建立了幾個分類器？像上面5類就建立了5個分類器吧，好了到了這我們該怎麽劃分測試集的樣本屬於哪一類了？註意測試集是假設不知道類標簽的，那麽來了一個測試樣本，我把它依次輸入到上述建立的5個分類器中，看看最終它屬於哪一類的多，那它就屬於哪一類了吧。比如假設一個測試樣本本來是屬於中間的（假設為第5類吧），那麽先輸入第五類自成一類的情況，這個時候發現它屬於第五類，記錄一下5，然後再輸入左上角（假設為1類）自成一類的情況，那麽發現這個樣本時不屬於1類的，而是屬於2,3,4,5這幾類合並在一起的一類中，那麽它屬於2,3,4,5中的誰呢？都有可能吧，那麽我都記一下，此時記一下2,3,4,5。好了再到有上角，此時又可以記一下這個樣本輸入1,3,4,5.依次類推，最後把這5個分類器都走一遍，就記了好多1~5的標簽吧，然後去統計他們的數量，比如這裏統計1類，發現出現了3次，2,3,4都出現了3次，就5出現了5次，那麽我們就有理由認為這個樣本屬於第五類，那麽現在想想是不是就把多類問題解決了呢？而這個過程參考這位大神博客中的一張圖表示就如下：

可以看到，其實黑實線本類是我們想要的理想分類面，而按照這種方式建立的分類面是帶陰影部分的那個分類面，那陰影部分裏面表示什麽呢？我們想想，假設一個樣本落在了陰影裏面，比如我畫的那個紫色的點，按照上面計算，發現它屬於三角形一類的2次，屬於正方形一類的2次，屬於圓形一類的1次，那這個時候你怎麽辦？沒招，只能在最大的兩次中挑一個，運氣好的認為屬於三角形，挑對了，運氣不好的挑了個正方形，分錯了。所以陰影部分是屬於模棱兩可的情況，這個時候只能挑其中一個了。

這是第一種方式，那還有第二種分類方式，思想類似，也是轉化為二分類問題，不過實現上不同。前面我們是挑一類自成一類，剩下的所有自成一類，而這裏，也是從中挑一類自成一類，然剩下的並不是自成一類，而是在挑一類自成一類，也就是說從訓練樣本中挑其中的兩類來產生一個分類器。像上述的5類，我先把1,2,類的訓練樣本挑出來，訓練一個屬於1,2,類的分類器，然後把1,3,挑出來訓練一個分類器，再1,4再1,5再2,3,等等（註意2,1與1,2一樣的，所以省去了），那這樣5類樣本需要建立多少個分類器呢？n*(n-1)/2吧，這裏就是5*4/2=10個分類器，可以看到比上面的5個分類器多了5個。而且n越大，多的就越多。好了建立完分類器，剩下的問題同樣采取投票機制，來一個樣本，帶到1,2建立的發現屬於1，屬於1類的累加器加一下，帶到1,3建立的發現也屬於1，在加一下，等等等等。最後看看5個類的累加器哪個最大就屬於哪一類。那麽一個問題來了，會不會出現像上面那種情況，有兩個或者更多個累加器的值是一樣的呢？答案是有的，但是這種情況下，出現一樣的概率可比上述情況的概率小多了（比較是10個分類器來的結果，怎麽也得比你5個的要好吧），同樣一個示意圖如下：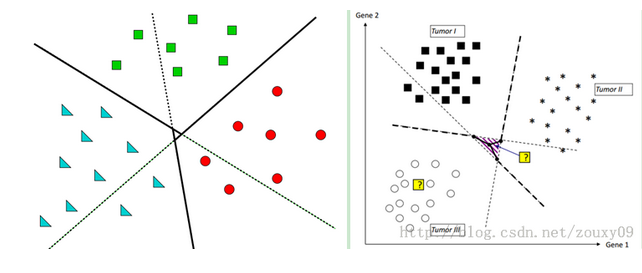

可以看到重疊部分就是中間那麽一小塊，相比上面那種方式小了不少吧。
那麽細比較這兩種方式，其實各有優缺點。第一種方式由於建立的分類器少（n越大越明顯吧，兩者相差(n*(n-1)/2 - n）個分類器）。也就是在運算的時候速度更快，而第二種方式雖然速度慢，但是精度高呀，而且現在計算機的速度也夠快了，可以彌補第二種方式的缺點，所以個人更傾向於第二種方式了。

在基於上述的兩個子函數下，我們在編寫兩個函數，一個是adaboost的訓練函數，一個是adaboost的預測函數，函數如下：
訓練函數：

function model = adaboost_train(label,data,iter)
[model.dim,model.direction,model.thresh,model.alpha] = ...
    adaBoostTrainDs(data,label,iter);
model.iter = iter;

預測函數：

function predict = adaboost_predict(data,model)
h = zeros(model.iter,1);
for j = 1:model.iter
    if model.direction(j) == -1
        if data(model.dim(j)) <= model.thresh(j)
            h(j) = -1;
        else
            h(j) = 1;
        end
    elseif model.direction(j) == 1
        if data(model.dim(j)) <= model.thresh(j)
            h(j) = 1;
        else
            h(j) = -1;
        end
    end
end
predict = sign(model.alpha‘*h);

有了這兩個函數我們就可以進行實驗了，這裏我們只以第二種方式的多分類為例，函數同上面的svm類似，只不過把那裏的訓練模型函數與預測函數改到我們這裏的這種，主函數如下：

%%  
% * adaboost
% * 多類非線性分類
% 
%% 
clc
clear
close all
%% Load data
% * 數據預處理
data = load(‘data_test.mat‘);%選擇訓練樣本個數
num_train = 200;
%構造隨機選擇序列
choose = randperm(length(data));
train_data = data(choose(1:num_train),:);
gscatter(train_data(:,1),train_data(:,2),train_data(:,3));
label_train = train_data(:,end);
test_data = data(choose(num_train+1:end),:);
label_test = test_data(:,end);
%% adaboost的構建與訓練
num = 0;
iter = 30;%規定弱分類器的個數
for i = 1:5-1 %5類
    for j = i+1:5 
        num = num + 1;
        %重新歸類
        index1 = find(label_train == i);
        index2 = find(label_train == j);
        label_temp = zeros((length(index1)+length(index2)),1);
        %svm需要將分類標簽設置為1與-1
        label_temp(1:length(index1)) = 1;
        label_temp(length(index1)+1:length(index1)+length(index2)) = -1;
        train_temp = [train_data(index1,:);train_data(index2,:)];
        % 訓練模型
        model{num} = adaboost_train(label_temp,train_temp,iter);
    end
end
% 用模型來預測測試集的分類
predict = zeros(length(test_data),1);
for i = 1:length(test_data)
    data_test = test_data(i,:);
    num = 0;
    addnum = zeros(1,5);
    for j = 1:5-1
        for k = j+1:5
            num = num + 1;
            temp = adaboost_predict(data_test,model{num});
            if temp > 0
                addnum(j) = addnum(j) + 1;
            else
                addnum(k) = addnum(k) + 1;
            end
        end
    end
    [~,predict(i)] = max(addnum);
end
%% show the result--testing
figure;
gscatter(test_data(:,1),test_data(:,2),predict);
accuracy = length(find(predict==label_test))/length(test_data);
title([‘predict the testing data and the accuracy is :‘,num2str(accuracy)]);

這還是在200個訓練樣本下300個測試樣本的一個結果如下：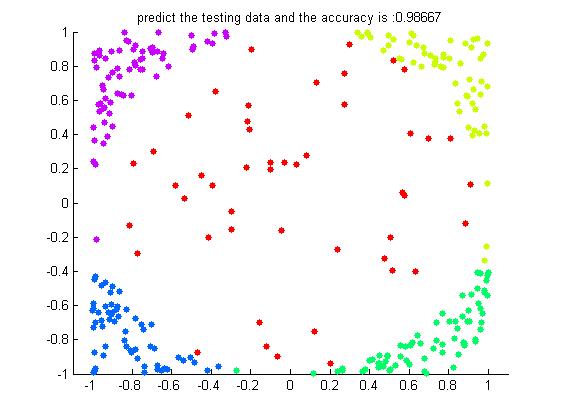

可以看到在iter=30個弱分類器下的結果已經是高的驚人了。

附上二分類數據集產生代碼：

%% % * Logistic方法用於回歸分析與分類設計 % * 多類問題的分類 % %% 產生非線性數據 2類 200個 clc clear close all data1 = rand(1,1000)*4 + 1; data2 = rand(1,1000)*4 + 1; circle_inx = data1 - 3; circle_iny = data2 - 3; r_in = circle_inx.^2 + circle_iny.^2; index_in = find(r_in<0.8); data_in = [data1(index_in(1:100));data2(index_in(1:100));-1*ones(1,100)]; data1 = rand(1,1000)*4 + 1; data2 = rand(1,1000)*4 + 1; circle_inx = data1 - 3; circle_iny = data2 - 3; r_in = circle_inx.^2 + circle_iny.^2; index_out = find((r_in>1.2)&(r_in<4)); data_out = [data1(index_out(1:100));data2(index_out(1:100));ones(1,100)]; plot(data_in(1,:),data_in(2,:),‘or‘); hold on; plot(data_out(1,:),data_out(2,:),‘*‘); data = [data_in,data_out]; save data_test1.mat data

特別翔實的adaboost分類算法講解 轉的