auc ks 新理解
轉https://www.zybuluo.com/frank-shaw/note/152851
新理解:我認為auc,和ks異曲同工。auc是根據預測概率(由大到小排序)作為閾值,可分割為不多於樣本個數n個閾值。即可得到n個recall和precision把這些點連成線即為roc曲線。auc即為roc下的面積。那個點最接近左上角即為最好的閾值。1和0作閾值分別得到(0,0)和(1,1)點。樣本點只是曲線上的點,理論上無窮大,不可能描繪完。橫:假陽率,縱:recall。n個點為相應閾值分割得到的recall和precision.
ks可認為也是根據預測概率(由大到小排序)作為閾值,橫軸為0到1的閾值,縱為n個recall和precision的點,分別繪制兩條曲線,他們之間的絕對差的最大值即為ks值,橫軸即為最好的閾值。
而根據金融上定義:ks是 1、根據預測值分區求原y值中各區的好壞占比(分區中好壞/比總的好壞)。 2、求好占比-壞占比的絕對差最大的值為ks值。 如:https://blog.csdn.net/u013421629/article/details/78217498
我認為這是不對的。如最大值可能是某個分區都是好的或壞的,這樣的值沒有意義。只有recall-假陽率絕對差最大才有實際意義。
前言
本文內容大部分來自於如下兩個博客:
http://blog.csdn.net/dinosoft/article/details/43114935
http://my.oschina.net/liangtee/blog/340317
引子
假設有下面兩個分類器,哪個好?(樣本中有A類樣本90個,B 類樣本10個。)
| 、 | A類樣本 | B類樣本 | 分類精度 |
|---|---|---|---|
| 分類器C1 | A*90(100%) | A*10(0%) | 90% |
| 分類器C2 | A*70 + B*20 (78%) | A*5 + B*5 (50%) | 75% |
分類器C1把所有的測試樣本都分成了A類,分類器C2把A類的90個樣本分對了70個,B類的10個樣本分對了5個。
則C1的分類精度為 90%,C2的分類精度為75%,但直覺上,我們感覺C2更有用些。但是依照正確率來衡量的話,那麽肯定C1的效果好一點。那麽這和我們認為的是不一致的。也就是說,有些時候,僅僅依靠正確率是不妥當的。
我們還需要一個評價指標,能客觀反映對正樣本、負樣本綜合預測的能力,還要考慮消除樣本傾斜的影響(其實就是歸一化之類的思想,實際中很重要,比如pv總是遠遠大於click),這就是auc指標能解決的問題。
ROC
為了理解auc,我們需要先來弄懂ROC。
先來看一個普遍的二分類問題的結果,預測值和實際值有4種組合情況,看下面的表格: 
我們定義一個變量:
看圖也就可以知道,TPR表示的就是預測正確且實際分類為正的數量 與 所有正樣本的數量的比例。--實際的正樣本中,正確預測的比例是多少?
FPR表示的是預測錯誤且實際分類為負的數量 與所有負樣本數量的比例。 --實際的負樣本當中,錯誤預測的比例是多少?
可以代入到上面的兩個分類器當中,可以得到下面的表格(分類器C1):
| 、 | 預測A | 預測B | 合計 |
|---|---|---|---|
| 實際A | 90 | 0 | 90 |
| 實際B | 10 | 0 | 10 |
TPR = FPR = 1.0.
分類器C2:
| 、 | 預測A | 預測B | 合計 |
|---|---|---|---|
| 實際A | 70 | 20 | 90 |
| 實際B | 5 | 5 | 10 |
TPR = 0.78, FPR = 0.5
那麽,以TPR為縱坐標,FPR為橫坐標畫圖,可以得到: 
上圖中藍色表示C1分類器,綠色表示C2分類器。可以知道,這個時候綠色的點比較靠近左上角,可以看做是分類效果較好。所以評估標準改為離左上角近的是好的分類器(考慮了正負樣本的綜合分類能力)。
一連串這樣的點構成了一條曲線,該曲線就是ROC曲線。而ROC曲線下的面積就是AUC(Area under the curve of ROC)。這就是AUC指標的由來。
如何畫ROC曲線
對於一個特定的分類器和測試數據集,顯然只能得到一個分類結果,即一組FPR和TPR結果,而要得到一個曲線,我們實際上需要一系列FPR和TPR的值才能得到這樣的曲線,這又是如何得到的呢?
可以通過分類器的一個重要功能“概率輸出”,即表示分類器認為某個樣本具有多大的概率屬於正樣本(或負樣本),來動態調整一個樣本是否屬於正負樣本(還記得當時阿裏比賽的時候有一個表示被判定為正樣本的概率的列麽?)
假如我們已經得到了所有樣本的概率輸出(屬於正樣本的概率),現在的問題是如何改變這個閾值(概率輸出)?我們根據每個測試樣本屬於正樣本的概率值從大到小排序。下圖是一個示例,圖中共有20個測試樣本,“Class”一欄表示每個測試樣本真正的標簽(p表示正樣本,n表示負樣本),“Score”表示每個測試樣本屬於正樣本的概率。 
接下來,我們從高到低,依次將“Score”值作為閾值,當測試樣本屬於正樣本的概率大於或等於這個閾值時,我們認為它為正樣本,否則為負樣本。舉例來說,對於圖中的第4個樣本,其“Score”值為0.6,那麽樣本1,2,3,4都被認為是正樣本,因為它們的“Score”值都大於等於0.6,而其他樣本則都認為是負樣本。每次選取一個不同的閾值,我們就可以得到一組FPR和TPR,即ROC曲線上的一點。這樣一來,我們一共得到了20組FPR和TPR的值,將它們畫在ROC曲線的結果如下圖: 
當我們將閾值設置為1和0時,分別可以得到ROC曲線上的(0,0)和(1,1)兩個點。將這些(FPR,TPR)對連接起來,就得到了ROC曲線。當閾值取值越多,ROC曲線越平滑。
--在阿裏比賽的時候還以為ROC是沒用的!!!!真的是有眼無珠啊!!!還是有疑惑的是:如何根據ROC來判定結果的好換呢?看哪個分類器更加接近左上角吧。同時,可以根據ROC來確定劃定正樣本的概率邊界選擇在哪裏比較合適!!!原來是這樣!!!!!!!!!
為什麽使用ROC
既然已經這麽多評價標準,為什麽還要使用ROC和AUC呢?因為ROC曲線有個很好的特性:當測試集中的正負樣本的分布變化的時候,ROC曲線能夠保持不變。在實際的數據集中經常會出現類不平衡(class imbalance)現象,即負樣本比正樣本多很多(或者相反),而且測試數據中的正負樣本的分布也可能隨著時間變化。下圖是ROC曲線和Precision-Recall曲線的對比: 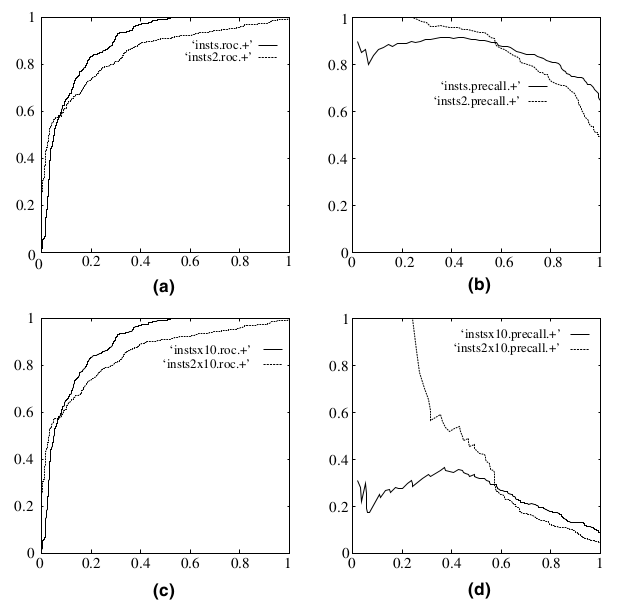
在上圖中,(a)和(c)為ROC曲線,(b)和(d)為Precision-Recall曲線。(a)和(b)展示的是分類其在原始測試集(正負樣本分布平衡)的結果,(c)和(d)是將測試集中負樣本的數量增加到原來的10倍後,分類器的結果。可以明顯的看出,ROC曲線基本保持原貌,而Precision-Recall曲線則變化較大。
auc ks 新理解
