題目鏈接

這次不咕了

https://www.luogu.org/problemnew/show/AT2389

閑扯

考場20分爆搜走人 \cy

話說這幾天T3都很考驗思維啊

分析

我們先欽定一只雞(雖然考試時是蘋果但是我覺得殺雞更親切(因為我們某位同學))先必須活著,所以呢我們需要逆著倒推每一組關系,然後把為了保證我們欽定的雞活著必須殺的雞放進一個集合,為了方便表示用\(f[now][i]=1/0\)表示欽定第now只雞活著第\(i\)只雞最終有沒有加入集合;

對於一對關系\((a,b)\),如果\(f[now][a]=1\),那麽\(f[now][b]\)顯然必須置為1加入集合,因為a這只雞為了保證now不被殺掉已經在一條邊中被殺掉,為了保證當前這條邊合法則必須殺掉b(註意關系是倒著枚舉的)

但這是有個問題,就是如果\(f[now][a]\)&\(f[now][b]=1\)說明關系矛盾,\(now\)必須死,為啥?

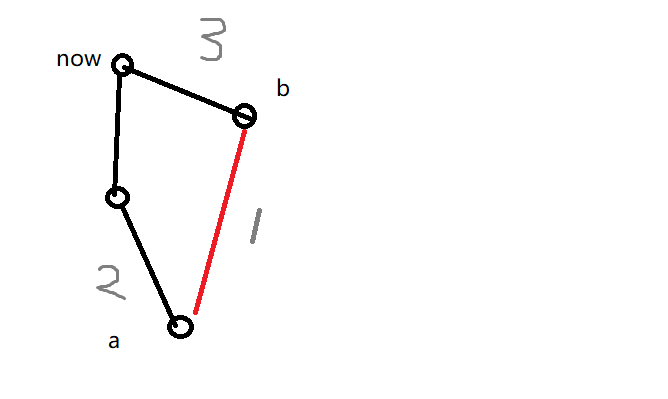
我們考慮沒有這種情況,將雞視為點,關系視為邊,顯然我們的集合實際上是一個以now為根節點的樹,而且滿足\(x\)到\(fa[x]\)的關系比\(fa[x]\)到\(fa[fa[x]]\)的邊次序要早(但是在枚舉時因為是倒著枚舉是先構成前者)

如果這時候加入一條邊連接兩個已經在集合中的點\((a,b)\),由於1號邊次序要比2,3邊早,所以先必須在a,b中選一個殺死滿足1號邊的關系.但是我們為了讓now不死,我們必須要讓a點因為2號邊死去,b因為3號邊死去.出現了這種情況顯然就不可能了,所以需要記錄一下\(now\)

最後假設已經遍歷完,獲得欽定每個點活著的時候要殺掉的雞的集合(雖然不一定合法)

然後對於每一只雞判斷是否能與編號靠後的另一只雞一起存活,怎麽判斷呢?

首先如果如果其中有只雞本身無法存活則特判continue,但是還有種非法的情況,就是存在一只雞為了滿足\(a\)活必須死,又同時滿足\(b\)活下來也必須死.這樣的話\(a,b\)無法同時存活

這其實很顯然的,邊有先後順序,你為了滿足其中一只雞另一只雞就一定不可行,所以這種情況我們可以把兩個雞的集合並起來看看有沒有1存在

代碼

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <iostream>
#include <bitset>
#define ll long long 
#define ri register int 
using std::min;
using std::bitset;
using std::max;
template <class T>inline void read(T &x){
    x=0;int ne=0;char c;
    while(!isdigit(c=getchar()))ne=c==‘-‘;
    x=c-48;
    while(isdigit(c=getchar()))x=(x<<3)+(x<<1)+c-48;
    x=ne?-x:x;return ;
}
const int maxn=405;
const int inf=0x7fffffff;
bitset <maxn> o[maxn];
bool ok[maxn];
int a[100005],b[100005],m,n;
int main(){
    int x,y;
    bool flag=0;
    read(n),read(m);
    for(ri i=1;i<=m;i++)read(a[i]),read(b[i]);
    for(ri i=1;i<=n;i++){
        o[i][i]=1;flag=0;
        for(ri j=m;j>=1&&!flag;j--){
            x=o[i][a[j]],y=o[i][b[j]];
            if(x&y){
                ok[i]=1;
                flag=1;continue;
            }
            if(x){o[i][b[j]]=1;}
            if(y){o[i][a[j]]=1;}
        }
    }
    ll ans=0;
    for(ri i=1;i<=n;i++){
        if(ok[i])continue;
        for(ri j=i+1;j<=n;j++){
            if(ok[j])continue;
            if(!((o[i]&o[j]).any()))ans++;
        }
    }
    printf("%lld\n",ans);
    return 0;
}
 

[NOIP10.5模擬賽]3.c題解--思維