簡單 輸出 壓縮 金字塔 特征 尺度 什麽 組成 sign

SIFT ：scale invariant feature transform

HOG：histogram of oriented gradients

這兩種方法都是基於圖像中梯度的方向直方圖的特征提取方法。

1. SIFT 特征

實現方法：

SIFT 特征通常與使用SIFT檢測器得到的感興趣點一起使用。這些感興趣點與一個特定的方向和尺度（scale）相關聯。通常是在對一個圖像中的方形區域通過相應的方向和尺度變換後，再計算該區域的SIFT特征。

首先計算梯度方向和幅值（使用Canny邊緣算子在感興趣點的周圍16X16像素點區域計算）。對得到的方向在0-360度範圍內分成八個區間，然後將16X16大小的區域分成不重合的4X4個單元，每個單元內計算梯度方向直方圖（八個區間）。一共得到16個單元的直方圖，將這些直方圖接連起來得到長度為128X1的向量，然後將該向量歸一化。

特點：

（1）由於使用梯度進行計算，該特征計算方法對恒定的灰度變化具有不變性。

（2）最後一步中的歸一化過程使該特征對圖像對比度具有一定不變性。

（3）由於在4X4的單元內計算直方圖，該特征不會受到一些小的形變的影響。

2. HOG 特征

實現方法：

HOG 特征 的實現方法與SIFT特征的實現方法類似，其廣泛用於行人檢測中。舉例來說，假如使用64X128的窗口進行檢測，先計算每個像素點處的梯度方向和幅值，梯度方向在0-180度範圍內被分成9個區間，64X128的區域被分成6X6大小的單元，每個單元內計算梯度方向直方圖。用3X3 個單元組成一個塊，在塊內將9個直方圖組合成一維向量後歸一化。然後將所有的塊得到的向量連接在一起得到最終的HOG 特征。

特點：

（1）單元的大小較小，故可以保留一定的空間分辨率。

（2）歸一化操作使該特征對局部對比度變化不敏感。

參考： http://blog.csdn.net/zouxy09/article/details/7929348

--------------------- 作者：飛躍重洋的思念 來源：CSDN 原文：https://blog.csdn.net/taigw/article/details/42206311?utm_source=copy 版權聲明：本文為博主原創文章，轉載請附上博文鏈接！

---

SIFT（Scale-invariant feature transform）是一種檢測局部特征的算法，該算法通過求一幅圖中的特征點（interest points,or corner points）及其有關scale 和 orientation 的描述子得到特征並進行圖像特征點匹配，獲得了良好效果，詳細解析如下：

算法描述

SIFT特征不只具有尺度不變性，即使改變旋轉角度，圖像亮度或拍攝視角，仍然能夠得到好的檢測效果。整個算法分為以下幾個部分：

1. 構建尺度空間

這是一個初始化操作，尺度空間理論目的是模擬圖像數據的多尺度特征。

高斯卷積核是實現尺度變換的唯一線性核，於是一副二維圖像的尺度空間定義為：

其中 G(x,y,σ) 是尺度可變高斯函數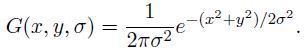

（x，y）是空間坐標，是尺度坐標。σ大小決定圖像的平滑程度，大尺度對應圖像的概貌特征，小尺度對應圖像的細節特征。大的σ值對應粗糙尺度(低分辨率)，反之，對應精細尺度(高分辨率)。為了有效的在尺度空間檢測到穩定的關鍵點，提出了高斯差分尺度空間（DOG scale-space）。利用不同尺度的高斯差分核與圖像卷積生成。

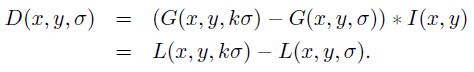
下圖所示不同σ下圖像尺度空間：

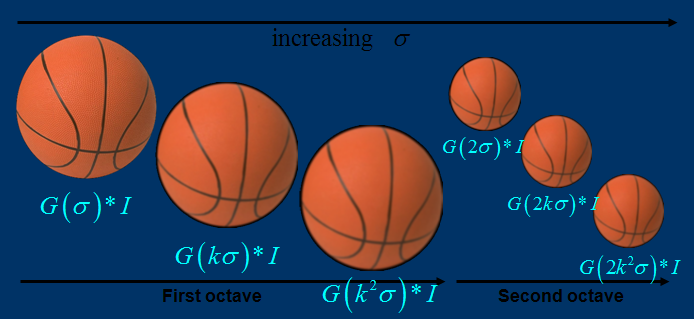
關於尺度空間的理解說明：2kσ中的2是必須的，尺度空間是連續的。在 Lowe的論文中 ，將第0層的初始尺度定為1.6（最模糊），圖片的初始尺度定為0.5（最清晰）. 在檢測極值點前對原始圖像的高斯平滑以致圖像丟失高頻信息，所以 Lowe 建議在建立尺度空間前首先對原始圖像長寬擴展一倍，以保留原始圖像信息，增加特征點數量。尺度越大圖像越模糊。

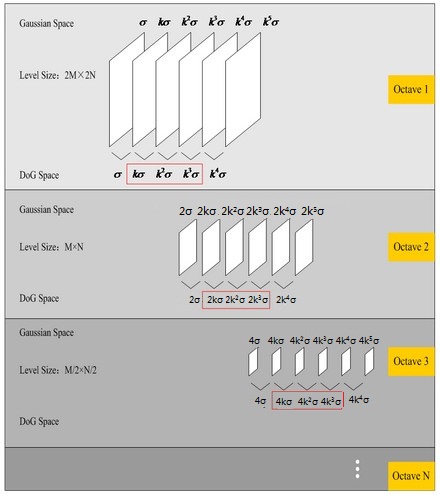
圖像金字塔的建立：對於一幅圖像I,建立其在不同尺度(scale)的圖像，也成為子八度（octave），這是為了scale-invariant，也就是在任何尺度都能夠有對應的特征點，第一個子八度的scale為原圖大小，後面每個octave為上一個octave降采樣的結果，即原圖的1/4（長寬分別減半），構成下一個子八度（高一層金字塔）。

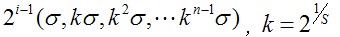
尺度空間的所有取值，i為octave的塔數（第幾個塔），s為每塔層數

由圖片size決定建幾個塔，每塔幾層圖像(S一般為3-5層)。0塔的第0層是原始圖像(或你double後的圖像)，往上每一層是對其下一層進行Laplacian變換（高斯卷積，其中σ值漸大，例如可以是σ, k*σ, k*k*σ…），直觀上看來越往上圖片越模糊。塔間的圖片是降采樣關系，例如1塔的第0層可以由0塔的第3層down sample得到，然後進行與0塔類似的高斯卷積操作。

2. LoG近似DoG找到關鍵點<檢測DOG尺度空間極值點>

為了尋找尺度空間的極值點，每一個采樣點要和它所有的相鄰點比較，看其是否比它的圖像域和尺度域的相鄰點大或者小。如圖所示，中間的檢測點和它同尺度的8個相鄰點和上下相鄰尺度對應的9×2個點共26個點比較，以確保在尺度空間和二維圖像空間都檢測到極值點。 一個點如果在DOG尺度空間本層以及上下兩層的26個領域中是最大或最小值時，就認為該點是圖像在該尺度下的一個特征點,如圖所示。

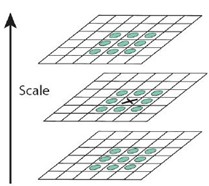
同一組中的相鄰尺度（由於k的取值關系，肯定是上下層）之間進行尋找

s=3的情況

在極值比較的過程中，每一組圖像的首末兩層是無法進行極值比較的，為了滿足尺度變化的連續性（下面有詳解） ，我們在每一組圖像的頂層繼續用高斯模糊生成了 3 幅圖像，高斯金字塔有每組S+3層圖像。DOG金字塔每組有S+2層圖像. ========================================== 這裏有的童鞋不理解什麽叫“為了滿足尺度變化的連續性”，現在做仔細闡述： 假設s=3，也就是每個塔裏有3層，則k=2^1/s=2^1/3，那麽按照上圖可得Gauss Space和DoG space 分別有3個（s個）和2個（s-1個）分量，在DoG space中，1st-octave兩項分別是σ,kσ; 2nd-octave兩項分別是2σ,2kσ;由於無法比較極值，我們必須在高斯空間繼續添加高斯模糊項，使得形成σ,kσ,k²σ,k³σ,k⁴σ這樣就可以選擇DoG space中的中間三項kσ,k²σ,k³σ（只有左右都有才能有極值），那麽下一octave中（由上一層降采樣獲得）所得三項即為2kσ,2k²σ,2k³σ，其首項2kσ=2^4/3。剛好與上一octave末項k³σ=2^3/3尺度變化連續起來，所以每次要在Gaussian space添加3項，每組（塔）共S+3層圖像，相應的DoG金字塔有S+2層圖像。 ==========================================

使用Laplacian of Gaussian能夠很好地找到找到圖像中的興趣點，但是需要大量的計算量，所以使用Difference of Gaussian圖像的極大極小值近似尋找特征點.DOG算子計算簡單，是尺度歸一化的LoG算子的近似,有關DOG尋找特征點的介紹及方法詳見http://blog.csdn.net/abcjennifer/article/details/7639488，極值點檢測用的Non-Maximal Suppression。

3. 除去不好的特征點

這一步本質上要去掉DoG局部曲率非常不對稱的像素。

通過擬和三維二次函數以精確確定關鍵點的位置和尺度（達到亞像素精度），同時去除低對比度的關鍵點和不穩定的邊緣響應點(因為DoG算子會產生較強的邊緣響應)，以增強匹配穩定性、提高抗噪聲能力，在這裏使用近似Harris Corner檢測器。

①空間尺度函數泰勒展開式如下：，對上式求導,並令其為0,得到精確的位置, 得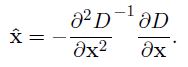

②在已經檢測到的特征點中,要去掉低對比度的特征點和不穩定的邊緣響應點。去除低對比度的點：把公式(2)代入公式(1)，即在DoG Space的極值點處D(x)取值，只取前兩項可得：

若 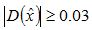，該特征點就保留下來，否則丟棄。

③邊緣響應的去除
一個定義不好的高斯差分算子的極值在橫跨邊緣的地方有較大的主曲率，而在垂直邊緣的方向有較小的主曲率。主曲率通過一個2×2 的Hessian矩陣H求出:

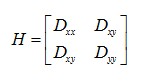
導數由采樣點相鄰差估計得到。

D的主曲率和H的特征值成正比，令α為較大特征值，β為較小的特征值，則

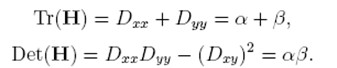
令α=γβ，則

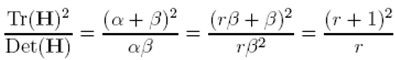
(r + 1)²/r的值在兩個特征值相等的時候最小，隨著r的增大而增大，因此，為了檢測主曲率是否在某域值r下，只需檢測

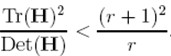
if (α+β)/ αβ> (r+1)²/r, throw it out. 在Lowe的文章中，取r＝10。

4. 給特征點賦值一個128維方向參數

上一步中確定了每幅圖中的特征點，為每個特征點計算一個方向，依照這個方向做進一步的計算， 利用關鍵點鄰域像素的梯度方向分布特性為每個關鍵點指定方向參數，使算子具備旋轉不變性。

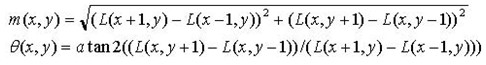
為(x,y)處梯度的模值和方向公式。其中L所用的尺度為每個關鍵點各自所在的尺度。至此，圖像的關鍵點已經檢測完畢，每個關鍵點有三個信息：位置，所處尺度、方向，由此可以確定一個SIFT特征區域。

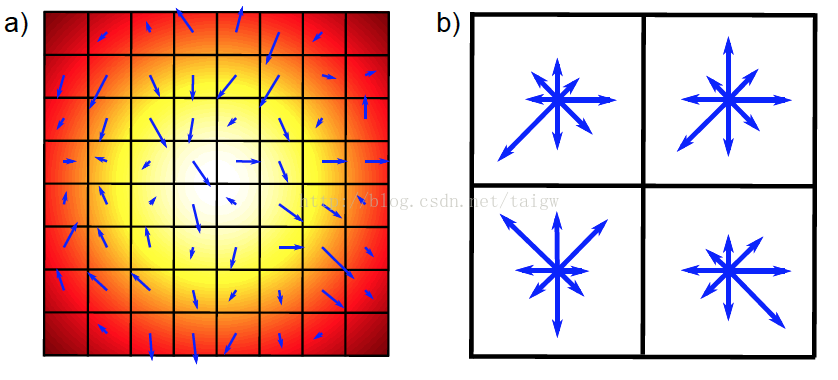
梯度直方圖的範圍是0～360度，其中每10度一個柱，總共36個柱。隨著距 中心點越遠的領域其對直方圖的貢獻也響應減小.Lowe論文中還提到要使用高斯函數對直方圖進行平滑，減少突變的影響。

在實際計算時，我們在以關鍵點為中心的鄰域窗口內采樣，並用直方圖統計鄰域像素的梯度方向。梯度直方圖的範圍是0～360度，其中每45度一個柱，總共8個柱, 或者每10度一個柱，總共36個柱。Lowe論文中還提到要使用高斯函數對直方圖進行平滑，減少突變的影響。直方圖的峰值則代表了該關鍵點處鄰域梯度的主方向，即作為該關鍵點的方向。

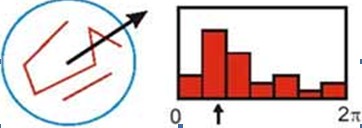
直方圖中的峰值就是主方向，其他的達到最大值80%的方向可作為輔助方向

由梯度方向直方圖確定主梯度方向

該步中將建立所有scale中特征點的描述子（128維）

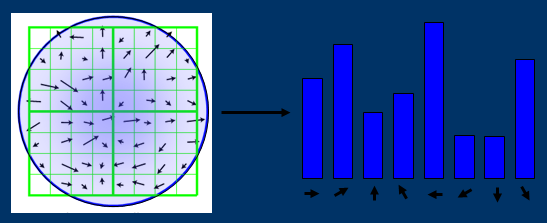
Identify peak and assign orientation and sum of magnitude to key point. The user may choose a threshold to exclude key points based on their assigned sum of magnitudes.

關鍵點描述子的生成步驟

通過對關鍵點周圍圖像區域分塊，計算塊內梯度直方圖，生成具有獨特性的向量，這個向量是該區域圖像信息的一種抽象，具有唯一性。

5. 關鍵點描述子的生成

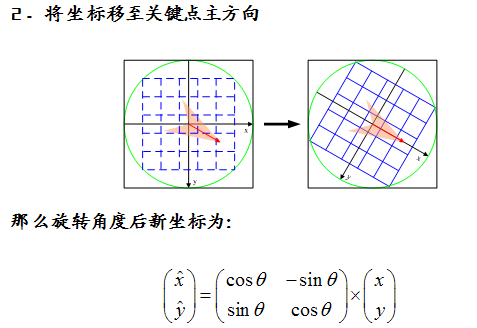
首先將坐標軸旋轉為關鍵點的方向，以確保旋轉不變性。以關鍵點為中心取8×8的窗口。

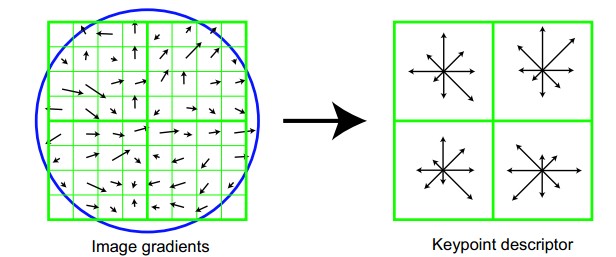
Figure.16*16的圖中其中1/4的特征點梯度方向及scale，右圖為其加權到8個主方向後的效果。

圖左部分的中央為當前關鍵點的位置，每個小格代表關鍵點鄰域所在尺度空間的一個像素，利用公式求得每個像素的梯度幅值與梯度方向，箭頭方向代表該像素的梯度方向，箭頭長度代表梯度模值，然後用高斯窗口對其進行加權運算。

圖中藍色的圈代表高斯加權的範圍（越靠近關鍵點的像素梯度方向信息貢獻越大）。然後在每4×4的小塊上計算8個方向的梯度方向直方圖，繪制每個梯度方向的累加值，即可形成一個種子點，如圖右部分示。此圖中一個關鍵點由2×2共4個種子點組成，每個種子點有8個方向向量信息。這種鄰域方向性信息聯合的思想增強了算法抗噪聲的能力，同時對於含有定位誤差的特征匹配也提供了較好的容錯性。

計算keypoint周圍的16*16的window中每一個像素的梯度，而且使用高斯下降函數降低遠離中心的權重。

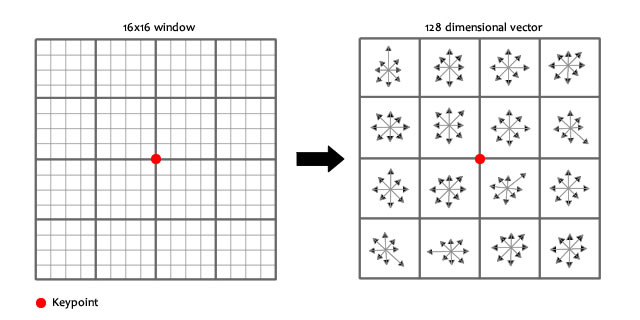
在每個4*4的1/16象限中，通過加權梯度值加到直方圖8個方向區間中的一個，計算出一個梯度方向直方圖。

這樣就可以對每個feature形成一個4*4*8=128維的描述子，每一維都可以表示4*4個格子中一個的scale/orientation. 將這個向量歸一化之後，就進一步去除了光照的影響。

5. 根據SIFT進行Match

生成了A、B兩幅圖的描述子，（分別是k1*128維和k2*128維），就將兩圖中各個scale（所有scale）的描述子進行匹配，匹配上128維即可表示兩個特征點match上了。

實際計算過程中，為了增強匹配的穩健性，Lowe建議對每個關鍵點使用4×4共16個種子點來描述，這樣對於一個關鍵點就可以產生128個數據，即最終形成128維的SIFT特征向量。此時SIFT特征向量已經去除了尺度變化、旋轉等幾何變形因素的影響，再繼續將特征向量的長度歸一化，則可以進一步去除光照變化的影響。 當兩幅圖像的SIFT特征向量生成後，下一步我們采用關鍵點特征向量的歐式距離來作為兩幅圖像中關鍵點的相似性判定度量。取圖像1中的某個關鍵點，並找出其與圖像2中歐式距離最近的前兩個關鍵點，在這兩個關鍵點中，如果最近的距離除以次近的距離少於某個比例閾值，則接受這一對匹配點。降低這個比例閾值，SIFT匹配點數目會減少，但更加穩定。為了排除因為圖像遮擋和背景混亂而產生的無匹配關系的關鍵點,Lowe提出了比較最近鄰距離與次近鄰距離的方法,距離比率ratio小於某個閾值的認為是正確匹配。因為對於錯誤匹配,由於特征空間的高維性,相似的距離可能有大量其他的錯誤匹配,從而它的ratio值比較高。Lowe推薦ratio的閾值為0.8。但作者對大量任意存在尺度、旋轉和亮度變化的兩幅圖片進行匹配，結果表明ratio取值在0. 4~0. 6之間最佳，小於0. 4的很少有匹配點，大於0. 6的則存在大量錯誤匹配點。(如果這個地方你要改進，最好給出一個匹配率和ration之間的關系圖，這樣才有說服力)作者建議ratio的取值原則如下:

ratio=0. 4　對於準確度要求高的匹配；
ratio=0. 6　對於匹配點數目要求比較多的匹配；
ratio=0. 5　一般情況下。
也可按如下原則:當最近鄰距離<200時ratio=0. 6，反之ratio=0. 4。ratio的取值策略能排分錯誤匹配點。

當兩幅圖像的SIFT特征向量生成後，下一步我們采用關鍵點特征向量的歐式距離來作為兩幅圖像中關鍵點的相似性判定度量。取圖像1中的某個關鍵點，並找出其與圖像2中歐式距離最近的前兩個關鍵點，在這兩個關鍵點中，如果最近的距離除以次近的距離少於某個比例閾值，則接受這一對匹配點。降低這個比例閾值，SIFT匹配點數目會減少，但更加穩定。

實驗結果：

Python+opencv實現：

1. import cv2
2. import numpy as np
3. #import pdb
4. #pdb.set_trace()#turn on the pdb prompt
6. #read image
7. img = cv2.imread(‘D:\privacy\picture\little girl.jpg‘,cv2.IMREAD_COLOR)
8. gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
9. cv2.imshow(‘origin‘,img);
11. #SIFT
12. detector = cv2.SIFT()
13. keypoints = detector.detect(gray,None)
14. img = cv2.drawKeypoints(gray,keypoints)
15. #img = cv2.drawKeypoints(gray,keypoints,flags = cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
16. cv2.imshow(‘test‘,img);
17. cv2.waitKey(0)
18. cv2.destroyAllWindows()

C實現：

1. // FeatureDetector.cpp : Defines the entry point for the console application.
2. //
3. // Created by Rachel on 14-1-12.
4. // Copyright (c) 2013年 ZJU. All rights reserved.
5. //
7. #include "stdafx.h"
8. #include "highgui.h"
9. #include "cv.h"
10. #include "vector"
11. #include "opencv\cxcore.hpp"
12. #include "iostream"
13. #include "opencv.hpp"
14. #include "nonfree.hpp"
15. #include "showhelper.h"
17. using namespace cv;
18. using namespace std;
20. int _tmain(int argc, _TCHAR* argv[])
21. {
22. //Load Image
23. Mat c_src1 = imread( "..\\Images\\3.jpg");
24. Mat c_src2 = imread("..\\Images\\4.jpg");
25. Mat src1 = imread( "..\\Images\\3.jpg", CV_LOAD_IMAGE_GRAYSCALE);
26. Mat src2 = imread( "..\\Images\\4.jpg", CV_LOAD_IMAGE_GRAYSCALE);
27. if( !src1.data || !src2.data )
28. { std::cout<< " --(!) Error reading images " << std::endl; return -1; }
30. //sift feature detect
31. SiftFeatureDetector detector;
32. std::vector<KeyPoint> kp1, kp2;
34. detector.detect( src1, kp1 );
35. detector.detect( src2, kp2 );
36. SiftDescriptorExtractor extractor;
37. Mat des1,des2;//descriptor
38. extractor.compute(src1,kp1,des1);
39. extractor.compute(src2,kp2,des2);
40. Mat res1,res2;
41. int drawmode = DrawMatchesFlags::DRAW_RICH_KEYPOINTS;
42. drawKeypoints(c_src1,kp1,res1,Scalar::all(-1),drawmode);//在內存中畫出特征點
43. drawKeypoints(c_src2,kp2,res2,Scalar::all(-1),drawmode);
44. cout<<"size of description of Img1: "<<kp1.size()<<endl;
45. cout<<"size of description of Img2: "<<kp2.size()<<endl;
47. //write the size of features on picture
48. CvFont font;
49. double hScale=1;
50. double vScale=1;
51. int lineWidth=2;// 相當於寫字的線條
52. cvInitFont(&font,CV_FONT_HERSHEY_SIMPLEX|CV_FONT_ITALIC, hScale,vScale,0,lineWidth);//初始化字體，準備寫到圖片上的
53. // cvPoint 為起筆的x，y坐標
54. IplImage* transimg1 = cvCloneImage(&(IplImage) res1);
55. IplImage* transimg2 = cvCloneImage(&(IplImage) res2);
57. char str1[20],str2[20];
58. sprintf(str1,"%d",kp1.size());
59. sprintf(str2,"%d",kp2.size());
62. const char* str = str1;
63. cvPutText(transimg1,str1,cvPoint(280,230),&font,CV_RGB(255,0,0));//在圖片中輸出字符
65. str = str2;
66. cvPutText(transimg2,str2,cvPoint(280,230),&font,CV_RGB(255,0,0));//在圖片中輸出字符
68. //imshow("Description 1",res1);
69. cvShowImage("descriptor1",transimg1);
70. cvShowImage("descriptor2",transimg2);
72. BFMatcher matcher(NORM_L2);
73. vector<DMatch> matches;
74. matcher.match(des1,des2,matches);
75. Mat img_match;
76. drawMatches(src1,kp1,src2,kp2,matches,img_match);//,Scalar::all(-1),Scalar::all(-1),vector<char>(),drawmode);
77. cout<<"number of matched points: "<<matches.size()<<endl;
78. imshow("matches",img_match);
79. cvWaitKey();
80. cvDestroyAllWindows();
82. return 0;
83. }

=============================== 基本概念及一些補充 什麽是局部特征？ 　　•局部特征從總體上說是圖像或在視覺領域中一些有別於其周圍的地方 　　•局部特征通常是描述一塊區域，使其能具有高可區分度 　　•局部特征的好壞直接會決定著後面分類、識別是否會得到一個好的結果 局部特征需具備的特性 　　•重復性 　　•可區分性 　　•準確性 　　•數量以及效率 　　•不變性 局部特征提取算法-sift 　　•SIFT算法由D.G.Lowe 1999年提出，2004年完善總結。後來Y.Ke將其描述子部分用PCA代替直方圖的方式，對其進行改進。 　　•SIFT算法是一種提取局部特征的算法，在尺度空間尋找極值點，提取位置，尺度，旋轉不變量 　　•SIFT特征是圖像的局部特征，其對旋轉、尺度縮放、亮度變化保持不變性，對視角變化、仿射變換、噪聲也保持一定程度的穩定性。 　　•獨特性好，信息量豐富，適用於在海量特征數據庫中進行快速、準確的匹配。 　　•多量性，即使少數的幾個物體也可以產生大量SIFT特征向量。 　　•可擴展性，可以很方便的與其他形式的特征向量進行聯合。 尺度空間理論 　　•尺度空間理論目的是模擬圖像數據的多尺度特征 　　•其基本思想是在視覺信息圖像信息處理模型中引入一個被視為尺度的參數, 通過連續變化尺度參數獲得不同尺度下的視覺處理信息, 然後綜合這些信息以深入地挖掘圖像的本質特征。 描述子生成的細節 　　•以極值點為中心點，並且以此點所處於的高斯尺度sigma值作為半徑因子。對於遠離中心點的梯度值降低對其所處區域的直方圖的貢獻，防止一些突變的影響。 　　•每個極值點對其進行三線性插值，這樣可以把此極值點的貢獻均衡的分到直方圖中相鄰的柱子上 歸一化處理 　　•在求出4*4*8的128維特征向量後，此時SIFT特征向量已經去除了尺度變化、旋轉等幾何變形因素的影響。而圖像的對比度變化相當於每個像素點乘上一個因子，光照變化是每個像素點加上一個值，但這些對圖像歸一化的梯度沒有影響。因此將特征向量的長度歸一化，則可以進一步去除光照變化的影響。 　　•對於一些非線性的光照變化，SIFT並不具備不變性，但由於這類變化影響的主要是梯度的幅值變化，對梯度的方向影響較小，因此作者通過限制梯度幅值的值來減少這類變化造成的影響。 PCA-SIFT算法 　　•PCA-SIFT與標準SIFT有相同的亞像素位置，尺度和主方向。但在第4步計算描述子的設計，采用的主成分分析的技術。 　　•下面介紹一下其特征描述子計算的部分： 　　　　•用特征點周圍的41×41的像斑計算它的主元，並用PCA-SIFT將原來的2×39×39維的向量降成20維，以達到更精確的表示方式。 　　　　•它的主要步驟為，對每一個關鍵點：在關鍵點周圍提取一個41×41的像斑於給定的尺度，旋轉到它的主方向 ；計算39×39水平和垂直的梯度，形成一個大小為3042的矢量；用預先計算好的投影矩陣n×3042與此矢量相乘；這樣生成一個大小為n的PCA-SIFT描述子。

===============================

輔助資料：

===============================

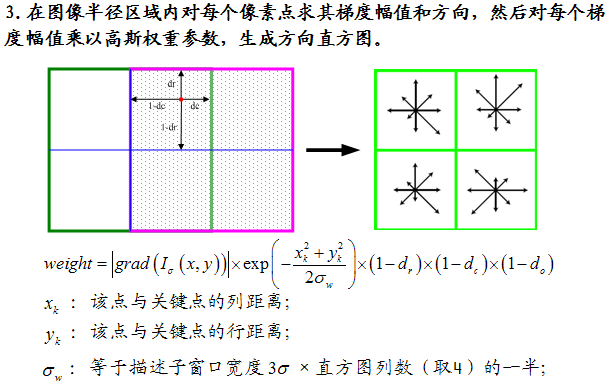
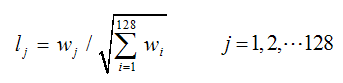
Reference:

Lowe SIFT 原文：http://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf

SIFT 的C實現：https://github.com/robwhess/opensift/blob/master/src

MATLAB 應用Sift算子的模式識別方法：http://blog.csdn.net/abcjennifer/article/details/7372880

http://blog.csdn.net/abcjennifer/article/details/7365882

http://en.wikipedia.org/wiki/Scale-invariant_feature_transform#David_Lowe.27s_method

http://blog.sciencenet.cn/blog-613779-475881.html

http://www.cnblogs.com/linyunzju/archive/2011/06/14/2080950.html

http://www.cnblogs.com/linyunzju/archive/2011/06/14/2080951.html

http://blog.csdn.net/ijuliet/article/details/4640624

http://www.cnblogs.com/cfantaisie/archive/2011/06/14/2080917.html (部分圖片有誤，以本文中的圖片為準)

--------------------- 作者：Rachel-Zhang 來源：CSDN 原文：https://blog.csdn.net/abcjennifer/article/details/7639681?utm_source=copy 版權聲明：本文為博主原創文章，轉載請附上博文鏈接！

---

1、HOG特征：

方向梯度直方圖（Histogram of Oriented Gradient, HOG）特征是一種在計算機視覺和圖像處理中用來進行物體檢測的特征描述子。它通過計算和統計圖像局部區域的梯度方向直方圖來構成特征。Hog特征結合SVM分類器已經被廣泛應用於圖像識別中，尤其在行人檢測中獲得了極大的成功。需要提醒的是，HOG+SVM進行行人檢測的方法是法國研究人員Dalal在2005的CVPR上提出的，而如今雖然有很多行人檢測算法不斷提出，但基本都是以HOG+SVM的思路為主。

（1）主要思想：

在一副圖像中，局部目標的表象和形狀（appearance and shape）能夠被梯度或邊緣的方向密度分布很好地描述。（本質：梯度的統計信息，而梯度主要存在於邊緣的地方）。

（2）具體的實現方法是：

首先將圖像分成小的連通區域，我們把它叫細胞單元。然後采集細胞單元中各像素點的梯度的或邊緣的方向直方圖。最後把這些直方圖組合起來就可以構成特征描述器。

（3）提高性能：

把這些局部直方圖在圖像的更大的範圍內（我們把它叫區間或block）進行對比度歸一化（contrast-normalized），所采用的方法是：先計算各直方圖在這個區間（block）中的密度，然後根據這個密度對區間中的各個細胞單元做歸一化。通過這個歸一化後，能對光照變化和陰影獲得更好的效果。

（4）優點：

與其他的特征描述方法相比，HOG有很多優點。首先，由於HOG是在圖像的局部方格單元上操作，所以它對圖像幾何的和光學的形變都能保持很好的不變性，這兩種形變只會出現在更大的空間領域上。其次，在粗的空域抽樣、精細的方向抽樣以及較強的局部光學歸一化等條件下，只要行人大體上能夠保持直立的姿勢，可以容許行人有一些細微的肢體動作，這些細微的動作可以被忽略而不影響檢測效果。因此HOG特征是特別適合於做圖像中的人體檢測的。

2、HOG特征提取算法的實現過程：

大概過程：

HOG特征提取方法就是將一個image（你要檢測的目標或者掃描窗口）：

1）灰度化（將圖像看做一個x,y,z（灰度）的三維圖像）；

2）采用Gamma校正法對輸入圖像進行顏色空間的標準化（歸一化）；目的是調節圖像的對比度，降低圖像局部的陰影和光照變化所造成的影響，同時可以抑制噪音的幹擾；

3）計算圖像每個像素的梯度（包括大小和方向）；主要是為了捕獲輪廓信息，同時進一步弱化光照的幹擾。

4）將圖像劃分成小cells（例如6*6像素/cell）；

5）統計每個cell的梯度直方圖（不同梯度的個數），即可形成每個cell的descriptor；

6）將每幾個cell組成一個block（例如3*3個cell/block），一個block內所有cell的特征descriptor串聯起來便得到該block的HOG特征descriptor。

7）將圖像image內的所有block的HOG特征descriptor串聯起來就可以得到該image（你要檢測的目標）的HOG特征descriptor了。這個就是最終的可供分類使用的特征向量了。

具體每一步的詳細過程如下：

（1）標準化gamma空間和顏色空間

為了減少光照因素的影響，首先需要將整個圖像進行規範化（歸一化）。在圖像的紋理強度中，局部的表層曝光貢獻的比重較大，所以，這種壓縮處理能夠有效地降低圖像局部的陰影和光照變化。因為顏色信息作用不大，通常先轉化為灰度圖；

Gamma壓縮公式：

比如可以取Gamma=1/2；

（2）計算圖像梯度

計算圖像橫坐標和縱坐標方向的梯度，並據此計算每個像素位置的梯度方向值；求導操作不僅能夠捕獲輪廓，人影和一些紋理信息，還能進一步弱化光照的影響。

圖像中像素點(x,y)的梯度為：

最常用的方法是：首先用[-1,0,1]梯度算子對原圖像做卷積運算，得到x方向（水平方向，以向右為正方向）的梯度分量gradscalx，然後用[1,0,-1]^T梯度算子對原圖像做卷積運算，得到y方向（豎直方向，以向上為正方向）的梯度分量gradscaly。然後再用以上公式計算該像素點的梯度大小和方向。

（3）為每個細胞單元構建梯度方向直方圖

第三步的目的是為局部圖像區域提供一個編碼，同時能夠保持對圖像中人體對象的姿勢和外觀的弱敏感性。

我們將圖像分成若幹個“單元格cell”，例如每個cell為6*6個像素。假設我們采用9個bin的直方圖來統計這6*6個像素的梯度信息。也就是將cell的梯度方向360度分成9個方向塊，如圖所示：例如：如果這個像素的梯度方向是20-40度，直方圖第2個bin的計數就加一，這樣，對cell內每個像素用梯度方向在直方圖中進行加權投影（映射到固定的角度範圍），就可以得到這個cell的梯度方向直方圖了，就是該cell對應的9維特征向量（因為有9個bin）。

像素梯度方向用到了，那麽梯度大小呢？梯度大小就是作為投影的權值的。例如說：這個像素的梯度方向是20-40度，然後它的梯度大小是2（假設啊），那麽直方圖第2個bin的計數就不是加一了，而是加二（假設啊）。

細胞單元可以是矩形的（rectangular），也可以是星形的（radial）。

（4）把細胞單元組合成大的塊（block），塊內歸一化梯度直方圖

由於局部光照的變化以及前景-背景對比度的變化，使得梯度強度的變化範圍非常大。這就需要對梯度強度做歸一化。歸一化能夠進一步地對光照、陰影和邊緣進行壓縮。

作者采取的辦法是：把各個細胞單元組合成大的、空間上連通的區間（blocks）。這樣，一個block內所有cell的特征向量串聯起來便得到該block的HOG特征。這些區間是互有重疊的，這就意味著：每一個單元格的特征會以不同的結果多次出現在最後的特征向量中。我們將歸一化之後的塊描述符（向量）就稱之為HOG描述符。

區間有兩個主要的幾何形狀——矩形區間（R-HOG）和環形區間（C-HOG）。R-HOG區間大體上是一些方形的格子，它可以有三個參數來表征：每個區間中細胞單元的數目、每個細胞單元中像素點的數目、每個細胞的直方圖通道數目。

例如：行人檢測的最佳參數設置是：3×3細胞/區間、6×6像素/細胞、9個直方圖通道。則一塊的特征數為：3*3*9；

（5）收集HOG特征

最後一步就是將檢測窗口中所有重疊的塊進行HOG特征的收集，並將它們結合成最終的特征向量供分類使用。

（6）那麽一個圖像的HOG特征維數是多少呢？

順便做個總結：Dalal提出的Hog特征提取的過程：把樣本圖像分割為若幹個像素的單元（cell），把梯度方向平均劃分為9個區間（bin），在每個單元裏面對所有像素的梯度方向在各個方向區間進行直方圖統計，得到一個9維的特征向量，每相鄰的4個單元構成一個塊（block），把一個塊內的特征向量聯起來得到36維的特征向量，用塊對樣本圖像進行掃描，掃描步長為一個單元。最後將所有塊的特征串聯起來，就得到了人體的特征。例如，對於64*128的圖像而言，每16*16的像素組成一個cell，每2*2個cell組成一個塊，因為每個cell有9個特征，所以每個塊內有4*9=36個特征，以8個像素為步長，那麽，水平方向將有7個掃描窗口，垂直方向將有15個掃描窗口。也就是說，64*128的圖片，總共有36*7*15=3780個特征。

--------------------- 作者：zouxy09 來源：CSDN 原文：https://blog.csdn.net/zouxy09/article/details/7929348?utm_source=copy 版權聲明：本文為博主原創文章，轉載請附上博文鏈接！

SIFT（Scale-invariant feature transform） & HOG（histogram of oriented gradients）