總結來自這篇論文的第7章

註意力機制

註意力機制是一種在編碼器-解碼器結構中使用到的機制, 現在已經在多種任務中使用:

• 機器翻譯(Neural Machine Translation, NMT)
• 圖像描述(Image Captioning (translating an image to a sentence))
• 文本摘要(Summarization(translating to a more compact language))

而且也不再局限於編碼器-解碼器結構, 多種變體的註意力結構, 應用在各種任務中.

總的來說, 註意力機制應用在:

• 允許解碼器在序列中的多個向量中, 關註它所需要的信息, 是傳統的註意力機制的用法. 由於使用了編碼器多步輸出, 而不是使用對應步的單一定長向量, 因此保留了更多的信息.
• 作用於編碼器, 解決表征問題(例如Encoding Vector再作為其他模型的輸入), 一般使用自註意力(self-attention)

1. 編碼器-解碼器註意力機制

1.1 編碼器-解碼器結構

如上圖, 編碼器將輸入嵌入為一個向量, 解碼器根據這個向量得到輸出. 由於這種結構一般的應用場景(機器翻譯等), 其輸入輸出都是序列, 因此也被稱為序列到序列的模型Seq2Seq.

對於編碼器-解碼器結構的訓練, 由於這種結構處處可微, 因此模型的參數\(\theta\)可以通過訓練數據和最大似然估計得到最優解, 最大化對數似然函數以獲得最優模型的參數, 即:

\[\arg\max\limits_{\theta}\{\sum\limits_{(x,y)\in{corpus}}\log{p(y|x;\theta)}\}\]

這是一種端到端的訓練方法.

1.2 編碼器

原輸入通過一個網絡模型(CNN, RNN, DNN), 編碼為一個向量. 由於這裏研究的是註意力, 就以雙向RNN作為示例模型.

對於每個時間步\(t\), 雙向RNN編碼得到的向量\(h_t\)可以如下表示:

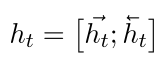
1.3 解碼器

這裏的解碼器是單向RNN結構, 以便在每個時間點上產生輸出, 行程序列. 由於解碼器僅使用最後時間步\(T\)對應的編碼器的隱藏向量\(h_{T_x}\), \(T_x\)指的是當前樣本的時間步長度(對於NLP問題, 經常將所有樣本處理成等長的). 這就迫使編碼器將更多的信息整合到最後的隱藏向量\(h_{T_x}\)中.

但由於\(h_{T_x}\)

註意力機制允許解碼器在每一個時間步\(t\)處考慮整個編碼器輸出的隱藏狀態序列\((h_1, h_2, \cdots, h_{T_x})\), 從而編碼器將更多的信息分散地保存在所有隱藏狀態向量中, 而解碼器在使用這些隱藏向量時, 就能決定對哪些向量更關心.

具體來說, 解碼器生產的目標序列\((y_1, \cdots, y_{T_x})\)中的每一個輸出(如單詞)\(y_t\), 都是基於如下的條件分布:

\[P[y_t|\{y_1,\cdots,y_{t-1}\},c_t]=softmax(W_s \tilde{h}_t)\]

其中\(\tilde{h}_t\)是引入註意力的隱藏狀態向量(attentional hidden state), 如下得到:

\[\tilde{h}_t=\tanh(W_c[c_t;h_t])\]

\(h_t\)為編碼器頂層的隱藏狀態, \(c_t\)是上下文向量, 是通過當前時間步上下文的隱藏向量計算得到的, 主要有全局和局部兩種計算方法, 下午中提到. \(W_c\)和\(W_s\)參數矩陣訓練得到. 為了式子的簡化沒有展示偏置項.

1.4 全局註意力

通過全局註意力計算上下文向量\(c_t\)時, 使用整個序列的隱藏向量\(h_t\), 通過加權和的方式獲得. 假設對於樣本\(x\)的序列長度為\(T_x\), \(c_t\)如下計算得到:

\[c_t=\sum\limits_{i=1}^{T_x}\alpha_{t,i}h_i\]

其中長度為\(T_x\)的校準向量alignment vector \(\alpha_t\)的作用是在\(t\)時間步, 隱藏狀態序列中的所有向量的重要程度. 其中每個元素\(\alpha_{t,i}\)的使用softmax方法計算:

\[\alpha_{t,i}=\frac{\exp(score(h_t, h_i))}{\sum\limits_{j=1}^{T_x}\exp(score(h_t, h_j))}\]

值的大小指明了序列中哪個時間步對預測當前時間步\(t\)的作用大小.

score函數可以是任意的比對向量的函數, 一般常用:

• 點積: \(score(h_t, h_i)=h_t^Th_i\)

  這在使用全局註意力時有更好的效果

• 使用參數矩陣:

  \(score(h_t, h_i)=h_t^TW_{\alpha}h_i\)

  這就相當於使用了一個全連接層, 這種方法在使用局部註意力時有更好的效果.

全局註意力的總結如下圖:

1.5 局部註意力

全局註意力需要在序列中所有的時間步上進行計算, 計算的代價是比較高的, 可以使用固定窗口大小的局部註意力機制, 窗口的大小為\(2D+1\). \(D\)為超參數, 為窗口邊緣距離中心的單方向距離. 上下文向量\(c_t\)的計算方法如下:

\[c_t=\sum\limits_{i=p_t-D}^{p_t+D}\alpha_{t,i}h_i\]

可以看到, 只是考慮的時間步範圍的區別, 其他完全相同. \(p_t\)作為窗口的中心, 可以直接使其等於當前時間步\(t\), 也可以設置為一個變量, 通過訓練獲得, 即:

\[p_t=T_x\sigma(v_p^T\tanh(W_ph_t))\]

其中\(\sigma\)為sigmoid函數, \(v_p\)和\(W_p\)均為可訓練參數. 因此這樣計算得到的\(p_t\)是一個浮點數, 但這並沒有影響, 因為計算校準權重向量\(\alpha_t\)時, 增加了一個均值為\(p_t\), 標準差為\(\frac{D}{2}\)的正態分布項:

\[\alpha_{t,i}=\frac{\exp(score(h_t, h_i))}{\sum\limits_{j=1}^{T_x}\exp(score(h_t, h_j))}\exp(-\frac{(i-p_t)^2}{2(D/2)^2})\]

當然, 這裏有\(p_t\in\mathbb{R}\cap[0, T_x]\), \(i\in\mathbb{N}\cap[p_t-D, p_t+D]\). 由於正態項的存在, 此時的註意力機制認為窗口中心附近的時間步對應的向量更重要, 且與全局註意力相比, 除了正態項還增加了一個截斷, 即一個截斷的正態分布.

局部註意力機制總結如下圖:

2. 自註意力

2.1 與編碼器-解碼器註意力機制的不同

最大的區別是自註意力模型沒有解碼器. 因此有兩個最直接的區別:

• 上下文向量\(c_t\)在seq2seq模型中, \(c_t=\sum\limits_{i=1}^{T_x}\alpha_{t,i}h_i\), 用來組成解碼器的輸入\[\tilde{h}_t=\tanh(W_c[c_t;h_t])\], 但由於自註意力機制沒有解碼器, 所以這裏就直接是模型的輸出, 即為\(s_t\)
• 在計算校準向量\(\alpha_t\)時, seq2seq模型使用的是各個位置的隱藏向量與當前隱藏向量的比較值. 在自註意力機制中, 校準向量中的每個元素由每個位置的隱藏向量與當前時間步\(t\)的平均最優向量計算得到的, 而這個平均最優向量是通過訓練得到的

2.2 自註意力機制實現

首先將隱藏向量\(h_i\)輸入至全連接層(權重矩陣為\(W\)), 得到\(u_i\):

\[u_i=\tanh(Wh_i)\]

使用這個向量計算校正向量\(\alpha_t\), 通過softmax歸一化得到:

\[\alpha_{t,i}=\frac{\exp(score(u_i, u_t))}{\sum\limits_{j=1}^{T_x}\exp(score(u_j, u_t))}\]

這裏的\(u_t\)是當前時間步\(t\)對應的平均最優向量, 每個時間步不同, 這個向量是通過訓練得到的.

最後計算最後的輸出:

\[s_t=\sum\limits_{i=1}^{T}a_{t, i}h_i\]

一般來說, 在序列問題中, 只關心最後時間步的輸出, 前面時間步不進行輸出, 即最後的輸出為\(s=s_T\)

2.3 層級註意力

如下圖, 對於一個NLP問題, 在整個架構中, 使用了兩個自註意力機制: 詞層面和句子層面. 符合文檔的自然層級結構:

詞->句子->文檔. 在每個句子中, 確定每個單詞的重要性, 在整片文檔中, 確定不同句子的重要性.

神經網絡中註意力機制概述