K. Random Numbers

time limit per test

2.0 s

memory limit per test

256 MB

input

standard input

output

standard output

Tamref love random numbers, but he hates recurrent relations, Tamref thinks that mainstream random generators like the linear congruent generator suck. That's why he decided to invent his own random generator.

As any reasonable competitive programmer, he loves trees. His generator starts with a tree with numbers on each node. To compute a new random number, he picks a rooted subtree and multiply the values of each node on the subtree. He also needs to compute the number of divisors of the generated number (because of cryptographical applications).

In order to modify the tree (and hence create different numbers on the future), Tamref decided to perform another query: pick a node, and multiply its value by a given number.

Given a initial tree T, where Tu corresponds to the value on the node u, the operations can be summarized as follows:

• RAND: Given a node u compute 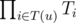 and count its divisors, where T(u) is the set of nodes that belong to the subtree rooted at u.
• SEED: Given a node u and a number x, multiply Tu by x.

Tamref is quite busy trying to prove that his method indeed gives integers uniformly distributed, in the meantime, he wants to test his method with a set of queries, and check which numbers are generated. He wants you to write a program that given the tree, and some queries, prints the generated numbers and count its divisors.

Tamref has told you that the largest prime factor of both Tu and x is at most the Tamref's favourite prime: 13. He also told you that the root of T is always node 0.

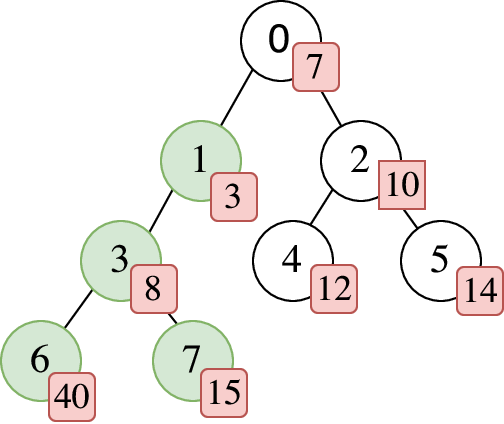
The figure shows the sample test case. The numbers inside the squares are the values on each node of the tree. The subtree rooted at node 1 is colored. The RAND query for the subtree rooted at node 1 would generate 14400, which has 63 divisors.

Input

The first line is an integer n (1 ≤ n ≤ 105), the number of nodes in the tree T. Then there are n - 1 lines, each line contains two integers uand v (0 ≤ u, v < n) separated by a single space, it represents that u is a parent of v in T. The next line contains n integers, where the i - th integer corresponds to Ti (1 ≤ Ti ≤ 109). The next line contains a number Q (1 ≤ Q ≤ 105), the number of queries. The final Q lines contain a query per line, in the form "RAND u" or "SEED u x" (0 ≤ u < n, 1 ≤ x ≤ 109).

Output

For each RAND query, print one line with the generated number and its number of divisors separated by a space. As this number can be very long, the generated number and its divisors must be printed modulo 109 + 7.

Example

input

Copy

8
0 1
0 2
1 3
2 4
2 5
3 6
3 7
7 3 10 8 12 14 40 15
3
RAND 1
SEED 1 13
RAND 1

output

Copy

14400 63
187200 126

題意：建一顆樹，查詢 所有以當前節點和所有兒子節點因子個數，更新，單點更新倍數。

題解：首先dfs把所有位置出現的序 排好。題目樣例 dfs,進入的先後順序 是

s[0]=1,s[1]=2,s[3]=2,s[6]=4,s[7]=5,s[2]=6,s[4]=7,s[5]=8;

然後保留每個節點最後一個所覆蓋的最大範圍如：

e[0]=8, 因為 0節點覆蓋了所有節點也就是 1-8 ，e[1]=5,1節點 覆蓋了所有序從 s[1]-e[1]（2 - 5）的節點。

然後以序建一顆線段樹：

查詢： x  每次查詢 [s[x],e[x]];

更新： x 每次更新 [ s[x] ,s[x] ];

我的線段樹每次儲存的是 (l,r]  ,所以 l 每次要-1。

 這題資料處理，每個節點保留所有素數因子個數，然後求的值就是所有素數的乘積，因子個數就是相應素數個數+1的乘積，

假如   素因子2有6個，素因子3有 2個 ，素因子5有2個，輸出就是    2^6*3^2*5^2,     7*3*3 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;

#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define mid (l+r)/2
#define chl 2*k+1
#define chr 2*k+2
#define lson l,mid,chl
#define rson mid,r,chr
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a));

const long long mod=1e9+7;
const int maxn=2e5+5;
const int INF=0x7fffffff;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
vector<int> G[maxn];
int e[maxn],s[maxn];
int val[maxn],val2[maxn];
int cnt=0;
int dfs(int r,int p) {
    cnt++;
//    debug(r);
    val[cnt]=val2[r];
    s[r]=cnt;
    for(int i=0; i<G[r].size(); i++) {
        int to=G[r][i];
        if(to!=p) {
            dfs(to,r);
        }
    }
    e[r]=cnt;
}

int dat[maxn<<4][6];
int prim[]= {2,3,5,7,11,13};
void init(int l,int r,int k) {
    if(r-l==1) {
        for(int i=0; i<6; i++) {
            while(val[r]%prim[i]==0) {
                val[r]/=prim[i];
                dat[k][i]++;
            }
        }
    } else {
        init(lson);
        init(rson);
        for(int i=0; i<6; i++) {
            dat[k][i]=dat[chl][i]+dat[chr][i];
        }
    }
}
void update(int a,int b,int l,int r,int k,ll x) {
    if(b<=l||a>=r) {
        return ;
    } else if(a<=l&&r<=b) {
        for(int i=0; i<6; i++) {
            while(x%prim[i]==0) {
                x/=prim[i];
                dat[k][i]++;
            }
        }
        return ;
    } else {
        update(a,b,lson,x);
        update(a,b,rson,x);
        for(int i=0; i<6; i++) {
            dat[k][i]=dat[chl][i]+dat[chr][i];
        }
    }
}
int res[6];
void query(int a,int b,int l,int r,int k) {
    if(b<=l||a>=r) {
        return ;
    } else if(a<=l&&r<=b) {
        for(int i=0; i<6; i++) {
            res[i]+=dat[k][i];
        }
    } else {
        query(a,b,lson);
        query(a,b,rson);
    }
}
long long pow(long long x,long long n,long long mod=1e9+7) {
    long long res=1;
    while(n>0) {
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res%mod;
}

int main() {
    int n;
    scanf("%d",&n);
    for(int i=1; i<n; i++) {
        int a,b;
        scanf("%d%d",&a,&b);
        G[a].push_back(b);
        G[b].push_back(a);
    }
    for(int i=0; i<n; i++) {
        scanf("%d",&val2[i]);
    }
    dfs(0,-1);
    init(0,n,0);
    int q;
    scanf("%d",&q);
    while(q--) {
        char ch[100];
        scanf("%s",ch);
        if(ch[0]=='R') {
            int a;
            scanf("%d",&a);
            mem(res,0);
            query(s[a]-1,e[a],0,n,0);
            ll ans=1,num=1;
            for(int i=0; i<6; i++) {
                ans*=pow(prim[i],res[i],mod);
                ans%=mod;
                num*=res[i]+1;
                num%=mod;
            }
            printf("%lld %lld\n",ans%mod,num%mod);
        } else {
            int a;
            ll b;
            scanf("%d%lld",&a,&b);
            update(s[a]-1,s[a],0,n,0,b);
        }
    }
    return 0;
}

0