要點

1、零極點圖繪製
2、根軌跡圖繪製
3、 rlocfind()函式
4、 sgrid()函式

實操

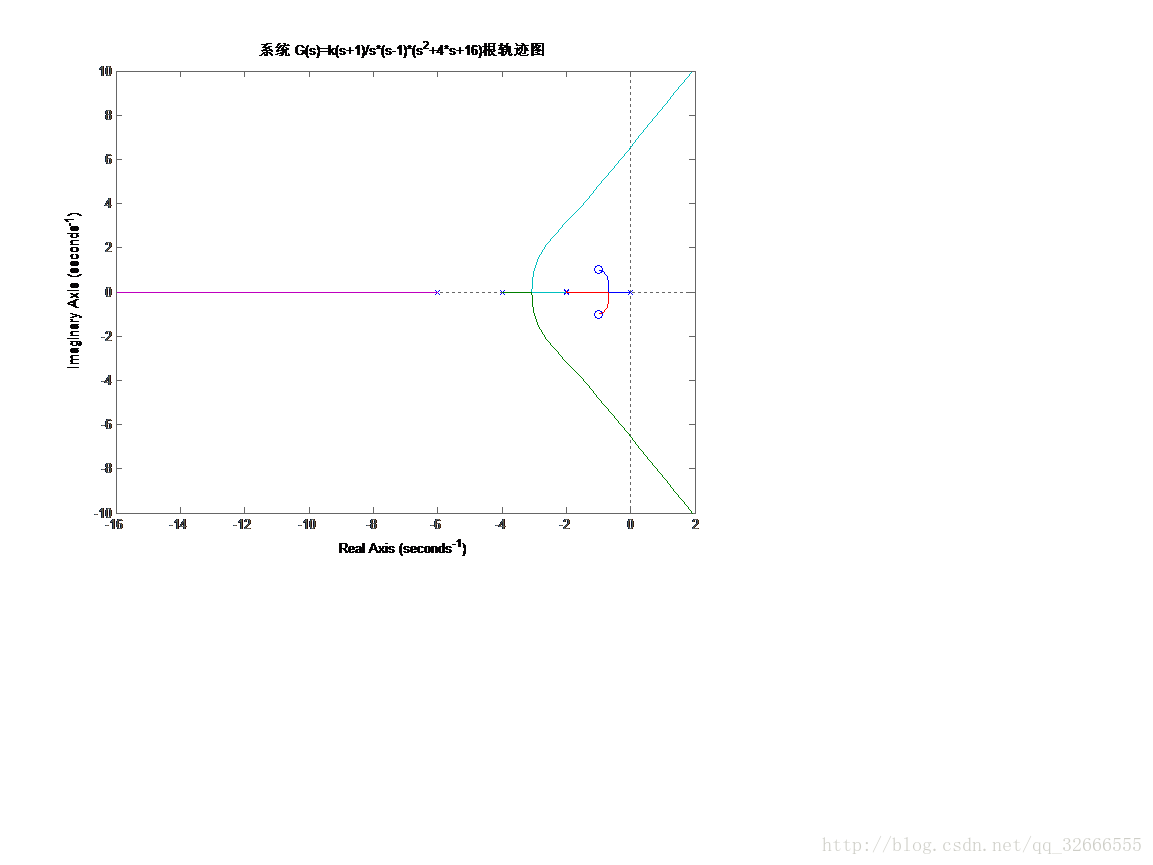
3-1

k=1;
num=[1 2 2];
den=conv([1,0],conv([1,4],conv([1,6],[1,4,4])));
[p,z]=pzmap(num,den)
G=zpk(z,p,k)
figure(1);pzmap(G)
figure(2);rlocus(G)
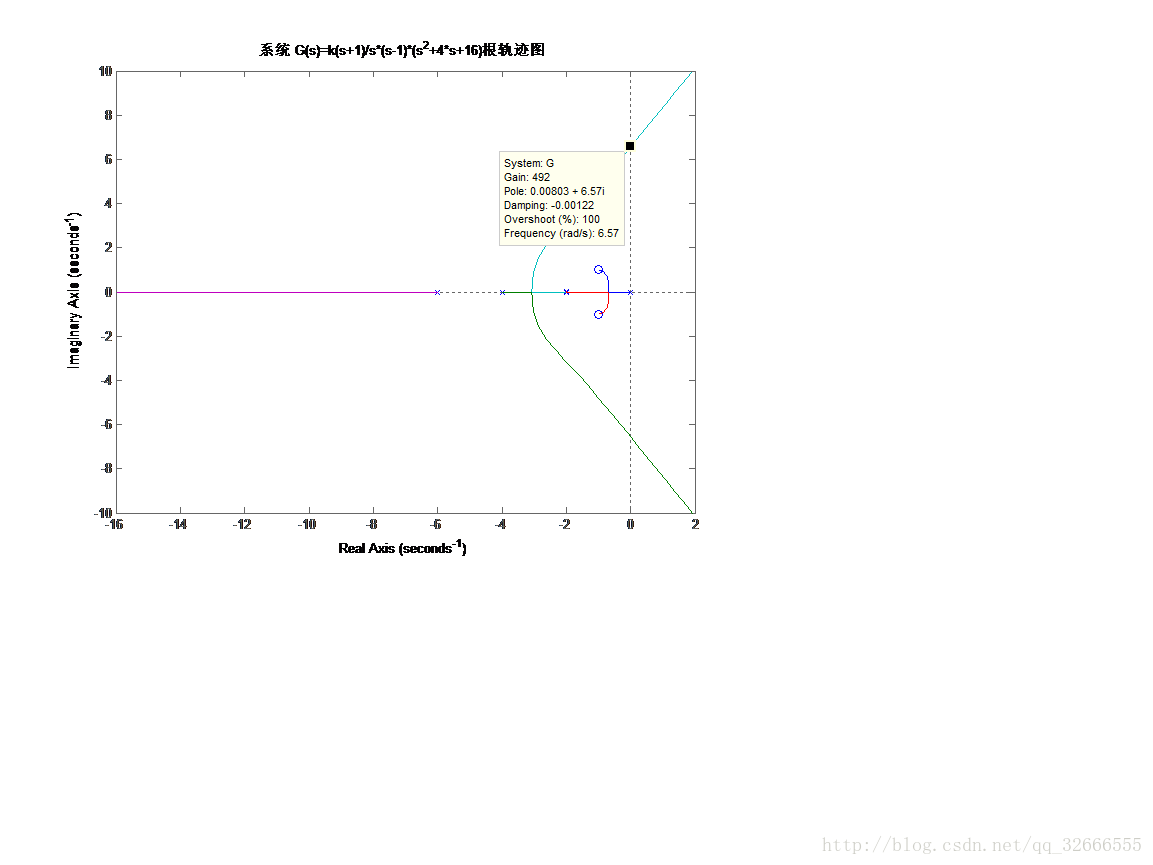
title('系統 G(s)=k(s+1)/s*(s-1)*(s^2+4*s+16)根軌跡圖');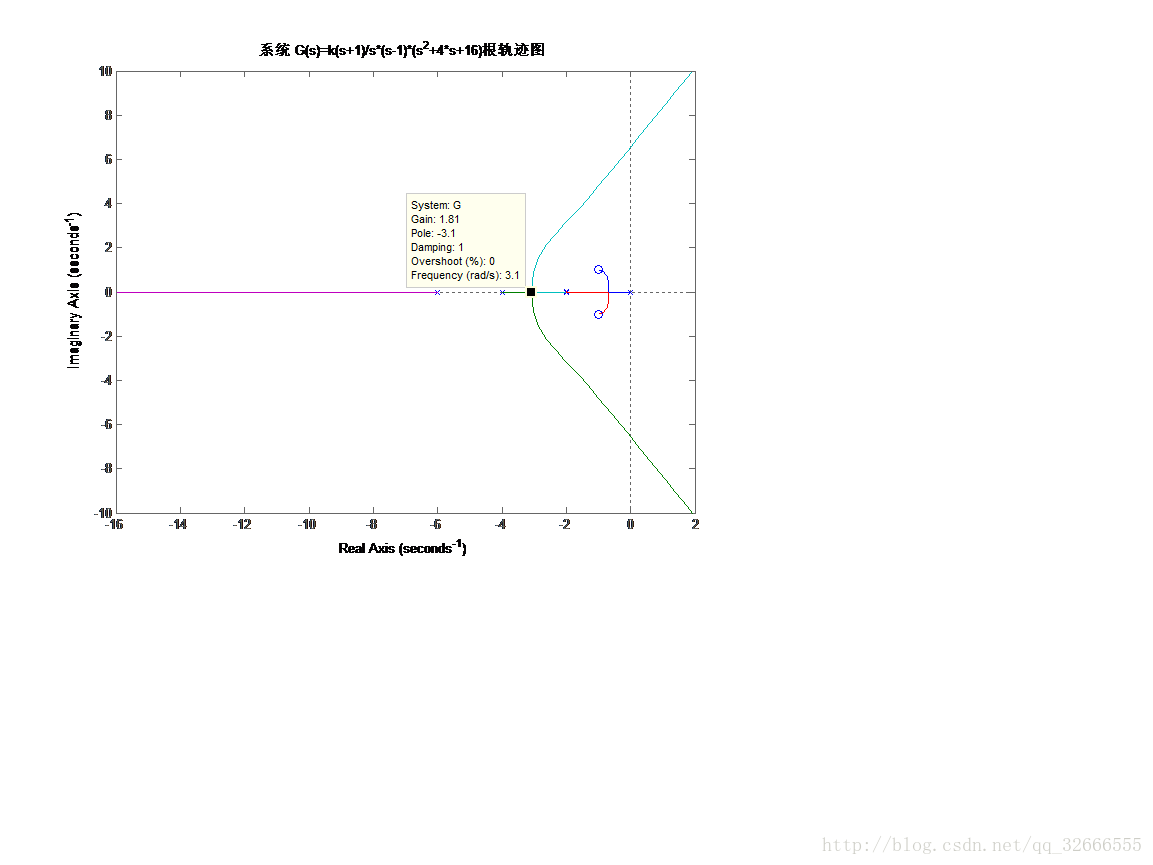

由圖得分離點 d=-3.1，相應的根軌跡增益 k=1.81

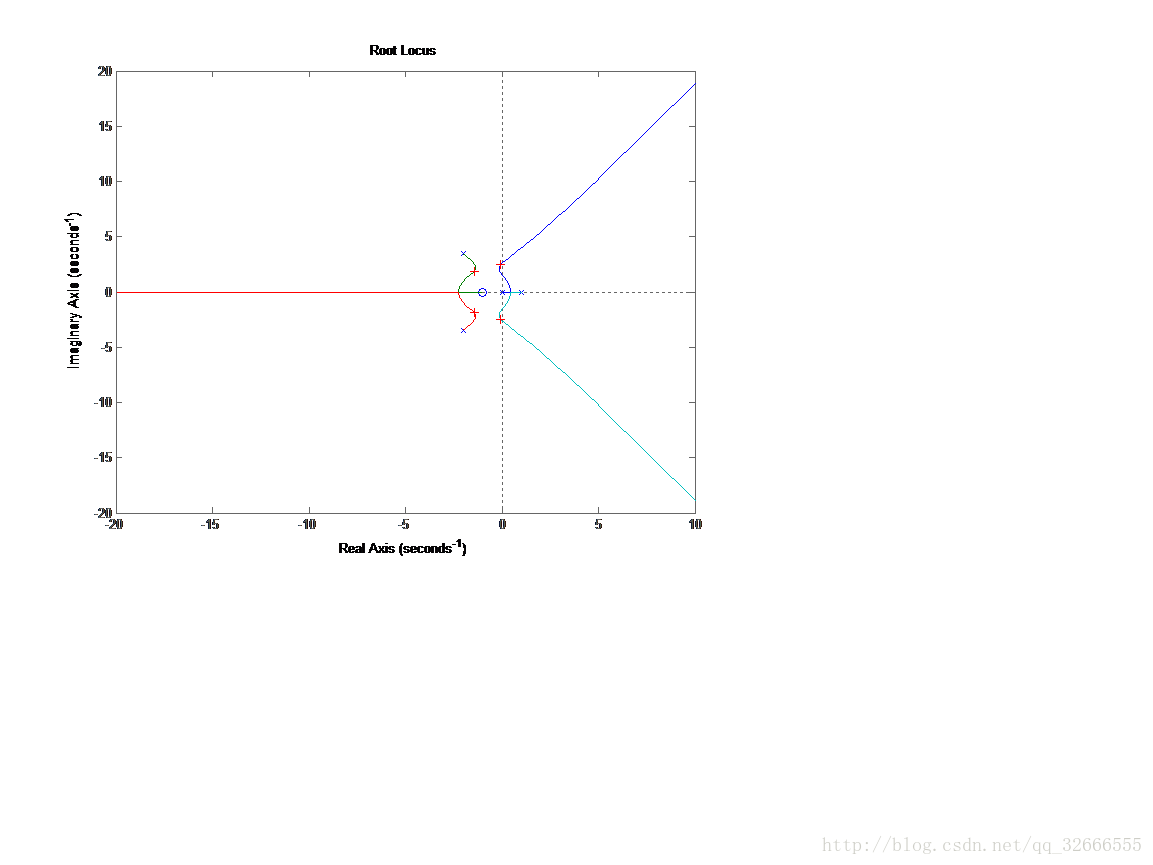
3-2

num=[1 1];
den=conv([1,0],conv([1,-1],[1,4,16]));
rlocus(num,den)
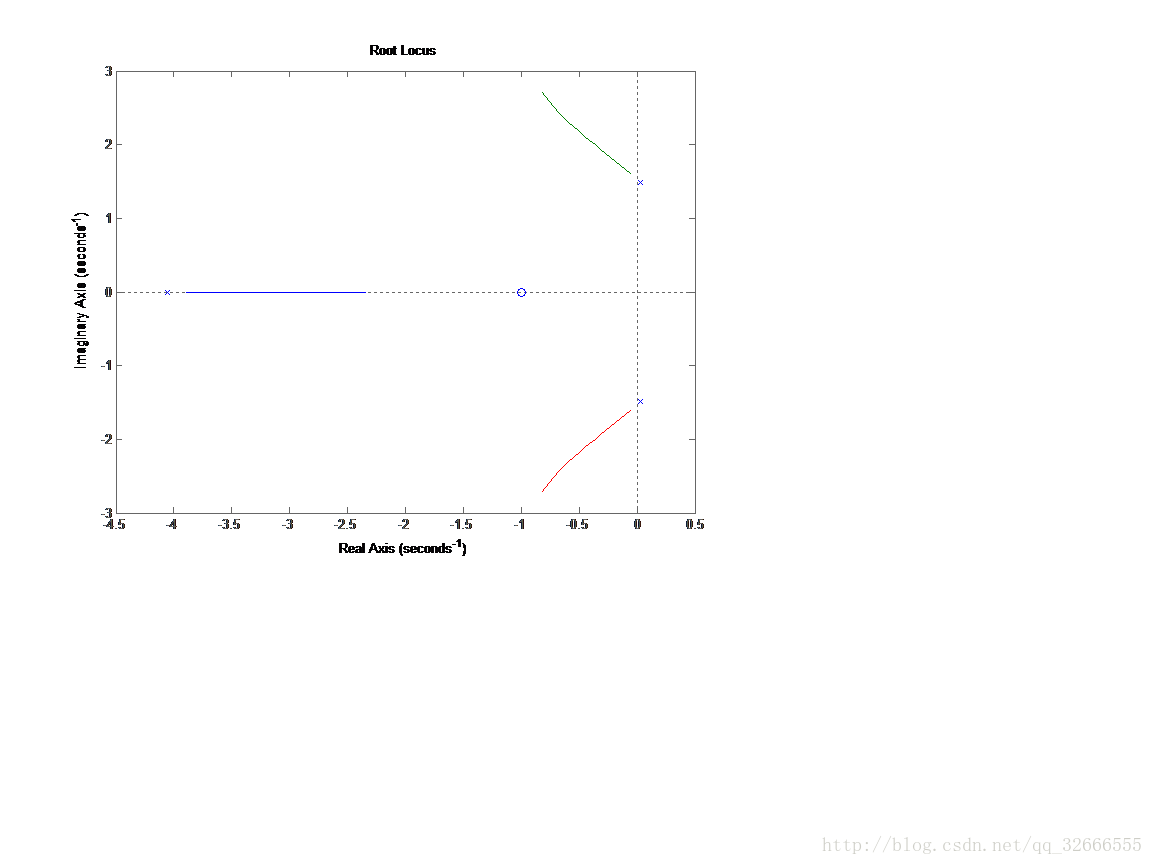
[k,p]=rlocfind(num,den)

呼叫rlocfind()函式，求出系統與虛軸交點的K值，可得與虛軸交點的K值為34.0224，故系統穩定的K的範圍為(0, 34.0224)

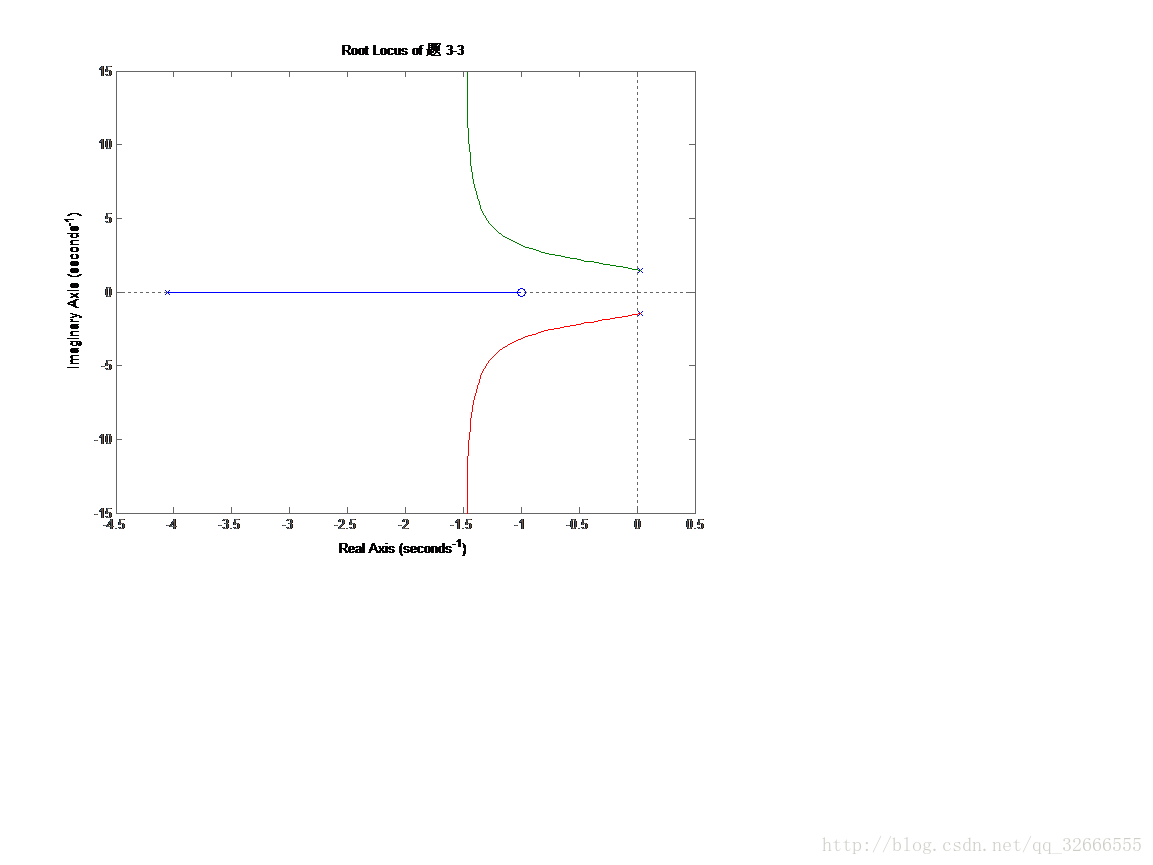
3-3

num=[1 1];
den=[1 4 2 9];
figure(1);rlocus(num,den)
title('Root Locus of 題 3-3');
k=1:0.5:10; 
figure(2
 
);rlocus (num,den,k)

3-4

z=[];
p=[0 0 -2 -5];
k=[1];
[num,den]=zp2tf(z,p,k); 
figure(1);rlocus(num,den)
z1=[-0.5];
[num1,den1]=zp2tf(z1,p,k); 
figure(2);rlocus(num1,den1)

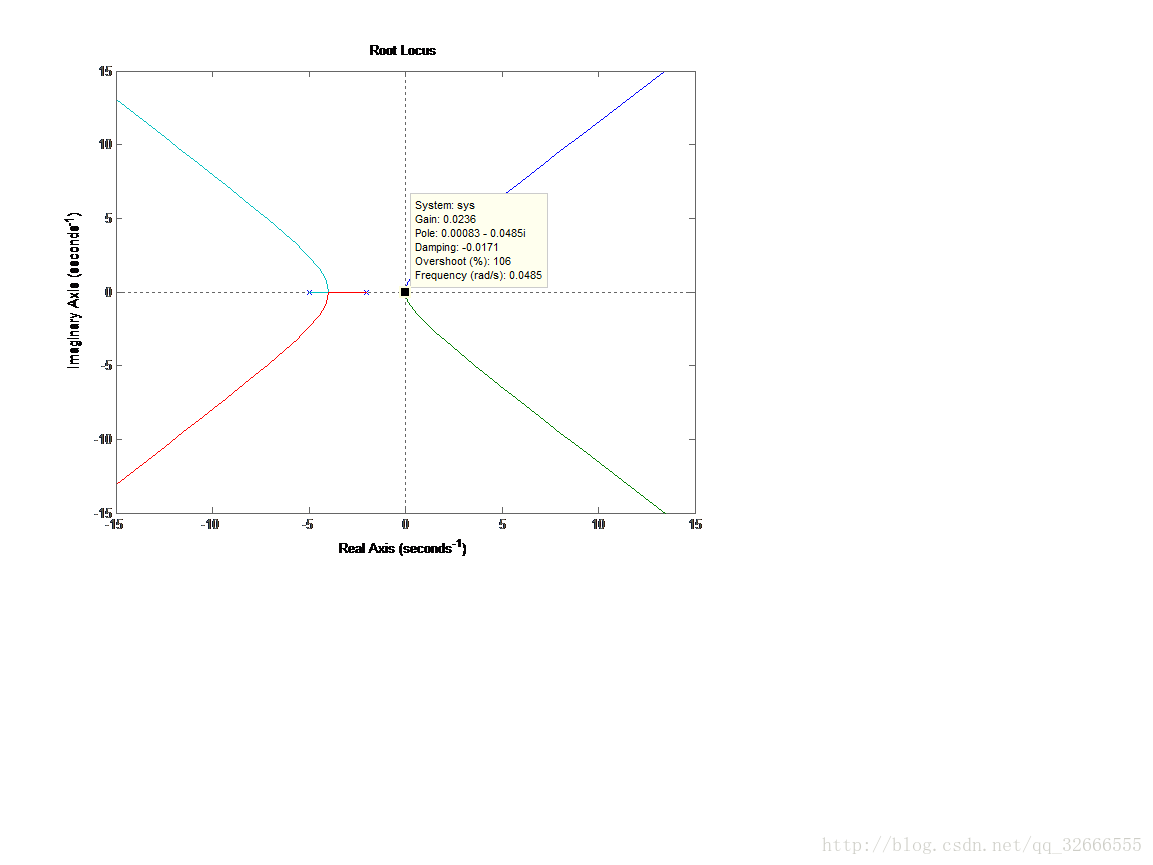
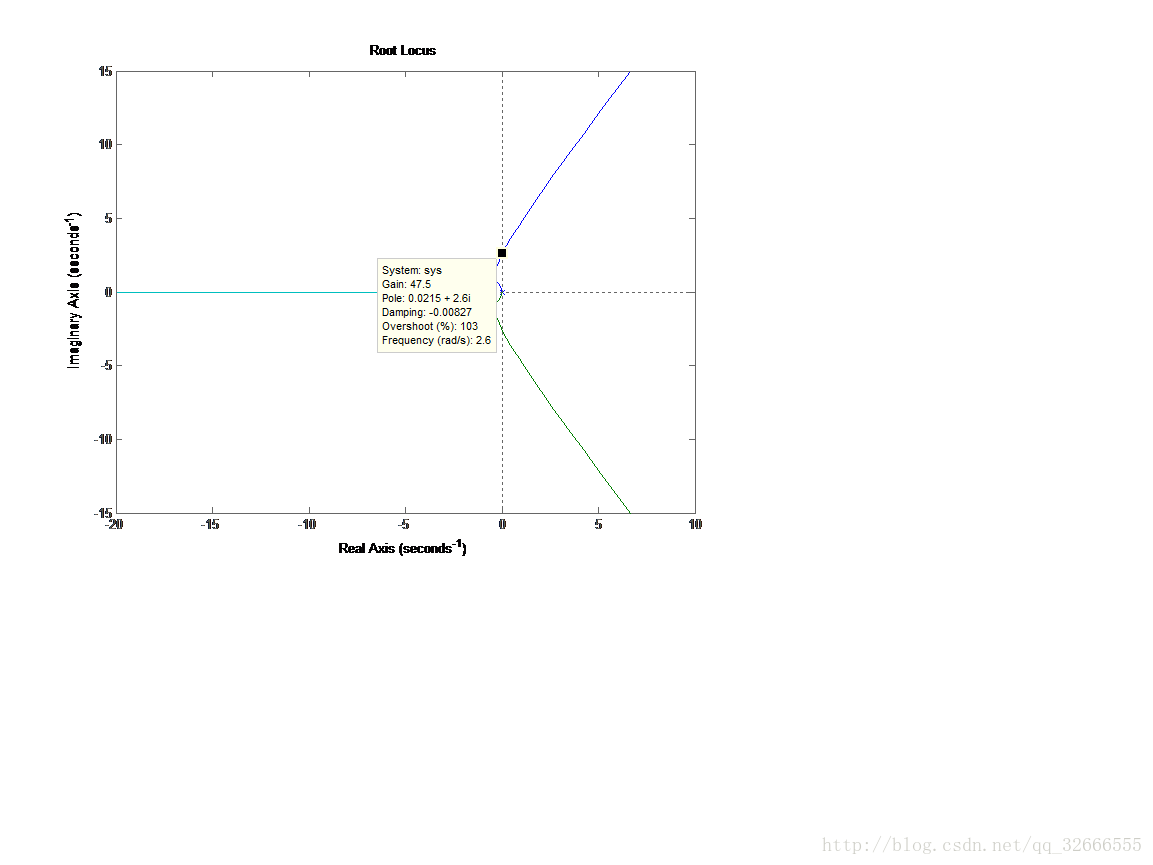
無論K取何值，系統都不穩定。

加入零點-0.5後，當K<47.5時，系統穩定。

分析：增加負零點後，系統根軌跡向S左半平面凹陷彎曲，，因此能夠一定地增強系統穩定性。