LeetCode[929,930,931,932]（周賽108）總結

本次周賽的地址為：https://leetcode-cn.com/contest/weekly-contest-108

文章目錄

• LeetCode[929,930,931,932]（周賽108）總結
• 929. 獨特的電子郵件地址
• 解題思路
• 程式碼：
• 優化程式碼：
• 930. 和相同的二元子陣列
• 解題思路
• 程式碼：
• 優化程式碼：
• 931. 下降路徑最小和
• 解題思路
• 錯誤程式碼：
• 正確程式碼：
• 932. 漂亮陣列
• 解題思路
• 正確程式碼：

929. 獨特的電子郵件地址

• 題目難度Easy

每封電子郵件都由一個本地名稱和一個域名組成，以 @ 符號分隔。

例如，在 [email protected]中， alice 是本地名稱，而 leetcode.com 是域名。

除了小寫字母，這些電子郵件還可能包含 ',' 或 '+'。

如果在電子郵件地址的本地名稱部分中的某些字元之間新增句點（'.'

），則發往那裡的郵件將會轉發到本地名稱中沒有點的同一地址。例如，"[email protected]” 和 “[email protected]” 會轉發到同一電子郵件地址。 （請注意，此規則不適用於域名。）

如果在本地名稱中新增加號（'+'），則會忽略第一個加號後面的所有內容。這允許過濾某些電子郵件，例如 [email protected] 將轉發到 [email protected]。 （同樣，此規則不適用於域名。）

可以同時使用這兩個規則。

給定電子郵件列表 emails，我們會向列表中的每個地址傳送一封電子郵件。實際收到郵件的不同地址有多少？

示例：

輸入：["[email protected]","[email protected]","[email protected]"]
輸出：2
解釋：實際收到郵件的是 "[email protected]" 和 "[email protected]"。

提示：

• 1 <= emails[i].length <= 100
• 1 <= emails.length <= 100
• 每封 emails[i] 都包含有且僅有一個 '@' 字元。

---

解題思路

這道題可以是一個比較簡單的字串題。主要就是先以@為間隔，將本地名稱和域名分割開。然後把字串的本地名稱部分的.給去掉，把+號後面的字元刪除。然後再和域名拼接到一起。判斷是否已經出現過後，通過一個list進行儲存。最後返回這個list的長度。

程式碼：

class Solution:
    def numUniqueEmails(self, emails):
        """
        :type emails: List[str]
        :rtype: int
        """
        list = []
        for email in emails:
            email1, email2 = email.split("@")
            email1 = email1.split("+")[0]
            email1 = email1.replace('.', '')
            email = email1 + '@' + email2
            if email not in list:
                list.append(email)
        return len(list)

其中，list的方式可以通過set()來進行一定的精簡。set是Python中的一個型別，它不包含重複的元素，會自動替我們判斷元素是否已出現，如果已經出現過了，則會自動將該元素刪除。

優化程式碼：

class Solution:
    def numUniqueEmails(self, emails):
        """
        :type emails: List[str]
        :rtype: int
        """
        list = set()
        for email in emails:
            email1, email2 = email.split("@")
            email1 = email1.replace('.', '').split("+")[0]
            email = email1 + '@' + email2
            list.add(email)
        return len(list)

---

930. 和相同的二元子陣列

• 題目難度Medium

在由若干 0 和 1 組成的陣列 A 中，有多少個和為 S 的非空子陣列。

示例：

輸入：A = [1,0,1,0,1], S = 2
輸出：4
解釋：
如下面黑體所示，有 4 個滿足題目要求的子陣列：
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]

提示：

1. A.length <= 30000
2. 0 <= S <= A.length
3. A[i] 為 0 或 1

---

解題思路

這道題的整體思路其實非常簡單，只需要遍歷一次陣列A，然後將當前的子陣列求和得到一個sum。

• 如果sum<S，則說明當前的子陣列不夠大，繼續向後遍歷。
• 如果sum ==S，則說明是符合條件的子陣列，計數器加一。同時，因為子陣列的頭部會出現有多個0元素的情況，而每去掉一個頭部的0元素，子陣列的和sum仍等於S。因此，還需要統計子陣列頭部0元素的個數。如果有n個0元素，則該情況下滿足要求的子陣列實際上有n+1個。
• 如果sum>S，則需要刪除子陣列第一個1元素及其之前的全部元素。再根據其頭部的0元素個數進行子陣列的數量統計。

程式碼：

class Solution:
    def numSubarraysWithSum(self, A, S):
        """
        :type A: List[int]
        :type S: int
        :rtype: int
        """
        l = []
        count = 0
        sum = 0
        for i in A:
            l.append(i)
            sum += i
            if sum > S:
                while l[0] == 0:
                    del l[0]
                del l[0]
                sum -= 1
            if sum == S:
                if 1 in l:
                    count += l.index(1) + 1
                else:
                    count += len(l)
        return count

通過閱讀這次周賽第一名選手cai_lw的程式碼，學習到了一個更加簡單的方式。

使用一個字典儲存陣列某個位置之前的陣列和，然後遍歷陣列求和，這樣當我們求到一個位置的和的時候，向前找sum-k是否在陣列中，如果在的話，更新結果為之前的結果+1。同時，當前這個sum出現的次數就多了一次。

優化程式碼：

from collections import defaultdict
class Solution:
    def numSubarraysWithSum(self, A, S):
        """
        :type A: List[int]
        :type S: int
        :rtype: int
        """
        d=defaultdict(lambda:0)
        ps=0
        ans=0
        for a in A:
            d[ps]+=1
            ps+=a
            ans+=d[ps-S]
        return ans

還是不是很理解這個思路。回頭繼續思考。

---

931. 下降路徑最小和

• 題目難度Medium

給定一個方形整數陣列 A，我們想要得到通過 A 的下降路徑的最小和。

下降路徑可以從第一行中的任何元素開始，並從每一行中選擇一個元素。在下一行選擇的元素和當前行所選元素最多相隔一列。

示例：

輸入：[[1,2,3],[4,5,6],[7,8,9]]
輸出：12
解釋：
可能的下降路徑有：

• [1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]
• [2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]
• [3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]

和最小的下降路徑是 [1,4,7]，所以答案是 12。

提示：

1. 1 <= A.length == A[0].length <= 100
2. -100 <= A[i][j] <= 100

---

解題思路

這是一個動態規劃的問題，我當時的思路是從第一層的節點開始，選擇下一層最小可以接觸到的最小節點進行連線，並迭代下去得到結果。

但是如果這樣做的話，得到的效果其實只是從第一層節點向下降能得到的最小路徑。

而在這個過程中，為了追求下層節點的最小值，而一起向值較小的下層節點靠攏，而忽略掉很多更優秀的路徑。

錯誤程式碼：

class Solution:
    def minFallingPathSum(self, A):
        """
        :type A: List[List[int]]
        :rtype: int
        """
        so = float("inf")
        for i in range(len(A[0])):
            do  = A[0][i]
            index = i
            for j in range(1, len(A)):
                if index == 0:
                    temp = min(A[j][index], A[j][index + 1])
                    index = A[j][index : index + 2].index(temp)
                    do += temp
                elif index == len(A[0]):
                    temp = min(A[j][index - 1], A[j][index])
                    index = A[j][index -1:].index(temp)
                    do += temp
                else:
                    temp = min(A[j][index -  1:index + 2])
                    index = A[j][index -1:index + 2].index(temp)
                    do += temp
            if do < so:
                so = do
        return so

而實際上這道動態規劃題目的解題思路應該為，以下一層的節點為目標，獲取到上一層可以接觸到的三個相鄰節點，並選擇最小的值進行連線。這樣做得到的結果就是：從第一層節點到當前位置的最小路徑。

用圖片來展示，即為下圖：

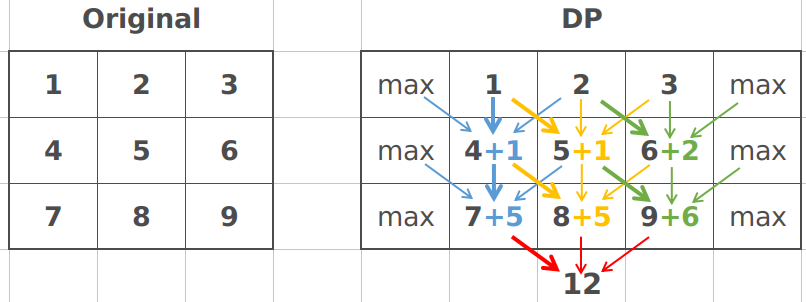
正確程式碼：

class Solution(object):
    def minFallingPathSum(self, A):
        """
        :type A: List[List[int]]
        :rtype: int
        """
        n = len(A)
        dp = A[0][::]
        for row in A[1:]:
            ndp = row[::]
            
            for i in range(n):
                candidates = [dp[i]]
                if i:
                    candidates.append(dp[i-1])
                if i != n-1:
                    candidates.append(dp[i+1])
                ndp[i] += min(candidates)
            dp = ndp
        return min(dp)

---

932. 漂亮陣列

• 題目難度Medium

對於某些固定的 N，如果陣列 A 是整數 1, 2, ..., N 組成的排列，使得：

對於每個 i < j，都不存在 k 滿足 i < k < j 使得 A[k] * 2 = A[i] + A[j]。

那麼陣列 A 是漂亮陣列。

給定 N，返回任意漂亮陣列 A（保證存在一個）。

示例 1：

輸入：4
輸出：[2,1,4,3]

示例 2：

輸入：5
輸出：[3,1,2,5,4]

提示：

• 1 <= N <= 1000

---

解題思路

我沒有理解的很透徹，因此就照搬他人的說法了。

可以先從題目的要求看：因為2*A[k]是偶數，所以只需要保證A[i]和A[j]為奇數和偶數，就可以滿足這個性質。

而如何在更長的陣列中滿足該性質呢？遞迴就可以了。其中有一個要點要注意。如果需要滿足題目的要求，則奇數的數量總是和偶數相等，或是更多的。因此，在構建的過程中，記得將奇數的那一部分設定為可能更大的那一部分進行遞迴。

至於遞迴的邊界條件N==1時，其實令這個元素的值等於任意整數似乎都可以，比如5，雖然這樣得到的陣列元素值很大，但是依然滿足條件。但是為了美觀，選擇令其為1即可。

正確程式碼：

class Solution(object):
    def beautifulArray(self, N):
        """
        :type N: int
        :rtype: List[int]
        """
        if N==1:
            return [1]
        else:
            l=self.beautifulArray(N//2)
            r=self.beautifulArray(N-N//2)
            return [x*2 for x in l]+[x*2-1 for x in r]