OpenGL ES 光照效果
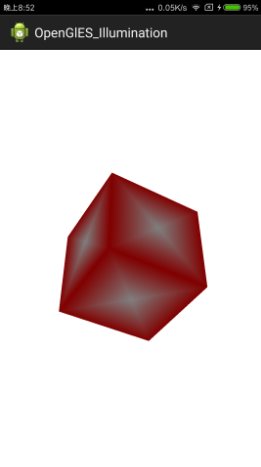
為了演示光照效果,在前面學習過的內容基礎上我們首先建立一個立方體,同時為了看起來直觀一些,這個立方體每個面採用中心為白色,周圍紅色的漸變方案,不然看上去同樣的顏色混在一起,看不出來是否是立方體。並且新增上轉動旋轉功能,這樣轉動起來立體感更強一些。
一個立方體
立方體類Rectangle.java
public class Rectangle {
private FloatBuffer mVertexBuffer;
private initVetexData類和前面的例子中基本一樣,但這裡和前面有一些不一樣的地方,在定義頂點時,發現裡面不僅定義了定點的座標,還定義了頂點的顏色,也就是座標和頂點放在了一個數據緩衝中,因此在讀取的時候,呼叫glVertexAttribPointer函式要注意stride引數傳入正確的值,並且在度去玩頂點座標值後,要將ByteBuffer的position重新置位到第一個顏色值開始的地方。
RectangleView.java
public class RectangleView extends GLSurfaceView{
private float mPreviousY;
private float mPreviousX;
MyRender mMyRender;
public RectangleView(Context context) {
super(context);
setEGLContextClientVersion(2);
mMyRender = new MyRender();
setRenderer(mMyRender);
}
public boolean onTouchEvent(MotionEvent e) {
float y = e.getY();
float x = e.getX();
switch (e.getAction()) {
case MotionEvent.ACTION_MOVE:
float dy = y - mPreviousY;
float dx = x - mPreviousX;
mMyRender.yAngle += dx;
mMyRender.xAngle+= dy;
requestRender();
}
mPreviousY = y;
mPreviousX = x;
return true;
}
class MyRender implements GLSurfaceView.Renderer {
private Rectangle mRectangle;
float yAngle;
float xAngle;
@Override
public void onSurfaceCreated(GL10 gl, EGLConfig config) {
GLES20.glClearColor(1, 1, 1, 1);
mRectangle = new Rectangle();
GLES20.glEnable(GLES20.GL_DEPTH_TEST);
}
@Override
public void onSurfaceChanged(GL10 gl, int width, int height) {
GLES20.glViewport(0, 0, width, height);
Matrix.perspectiveM(mProjectionMatrix, 0, 45, (float)width/height, 5, 15);
Matrix.setLookAtM(mViewMatrix, 0, 0, 0, 10, 0, 0, 0, 0, 1, 0);
}
private final float[] mProjectionMatrix = new float[16];
private final float[] mViewMatrix = new float[16];
private final float[] mModuleMatrix = new float[16];
private final float[] mViewProjectionMatrix = new float[16];
private final float[] mMVPMatrix = new float[16];
@Override
public void onDrawFrame(GL10 gl) {
GLES20.glClear( GLES20.GL_DEPTH_BUFFER_BIT | GLES20.GL_COLOR_BUFFER_BIT);
Matrix.setIdentityM(mModuleMatrix, 0);
Matrix.rotateM(mModuleMatrix, 0, xAngle, 1, 0, 0);
Matrix.rotateM(mModuleMatrix, 0, yAngle, 0, 1, 0);
Matrix.multiplyMM(mViewProjectionMatrix, 0, mProjectionMatrix, 0, mViewMatrix, 0);
Matrix.multiplyMM(mMVPMatrix, 0, mViewProjectionMatrix, 0, mModuleMatrix, 0);
mRectangle.draw(mMVPMatrix, mModuleMatrix);
}
}
}產生的效果
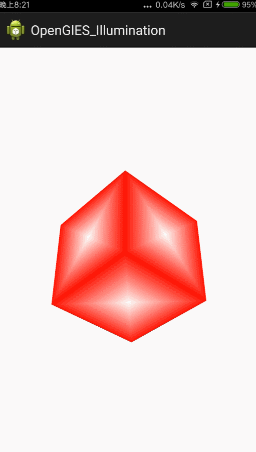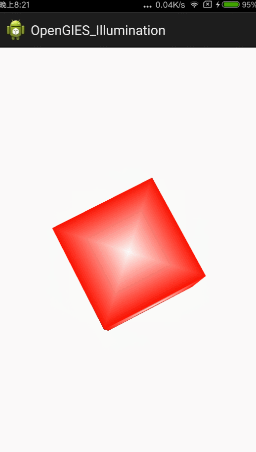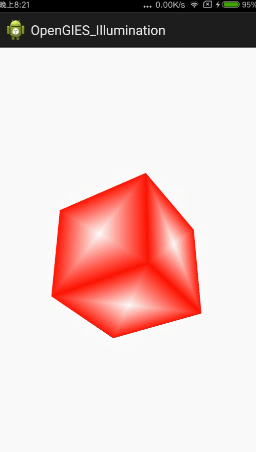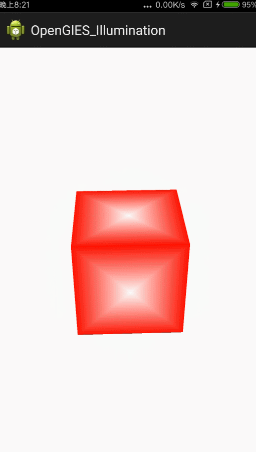
現在看起來感覺真實感還不是很強,因為自然界中還存在光照的影響。本篇文章就針對上面的立方體加入光照
光照模型
光照模型有三種,包括環境光、散射光和鏡面光。
環境光
環境光:從四面八方照射到物體上,全方位都均勻的光,代表的是現實世界中從廣元射出經過多次反射後各個方向基本均勻的光,環境光不依賴光源位置,而且沒有方向性。環境光入射均勻,反射也是均勻的。
環境光最終強度 = 環境光強度
修改片元著色器如下即可實現環境光的效果。
gl_FragColor = aaColor*vec4(0.5,0.5,0.5,1);加入環境光後的效果如下,可以看到效果很不好,畢竟每個地方的光照是一樣的,沒差別
散射光
散射光:從物體表面向全方位360度均勻反射的光,代表了現實世界中粗糙物體表面被光照射時,反射到各個方向基本均勻,也被稱為漫反射。散射光強度和入射角關係很大,入射角度越小,越亮。
其中
散射光的示意圖
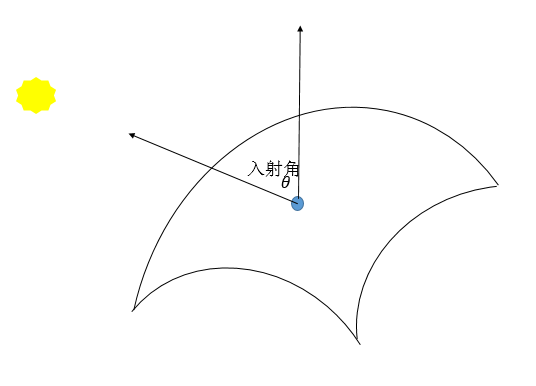
接下來主要修改頂點設色器的程式碼即可。
private String vertexShaderCode = "uniform mat4 uMVPMatrix;"
+ "uniform mat4 uMMatrix;" // 模型變換的矩陣
+ "uniform vec3 uLightLocation;" // 光源位置
+ "attribute vec4 aColor;"
+ "varying vec4 vColor;"
+ "varying vec4 vDiffuse;" // 傳遞給片元著色器的散射光強度,需要插值計算
+ "attribute vec3 aPosition;" // 頂點位置
+ "void main(){"
+ "vec3 normalVectorOrigin = aPosition;" // 原始採用點法向量
+ "vec3 normalVector = normalize((uMMatrix*vec4(normalVectorOrigin,1)).xyz);" // 歸一化的變換後的法向量
+ "vec3 vectorLight = normalize(uLightLocation - (uMMatrix * vec4(aPosition,1)).xyz);" // 歸一化的光源到點的向量
+ "float factor = max(0.0, dot(normalVector, vectorLight));"
+ "vDiffuse = factor*vec4(1,1,1,1.0);" // 散射光強度,需要插值計算
+ "gl_Position = uMVPMatrix * vec4(aPosition,1);"
+ "vColor = aColor;"
+ "}";片元著色器
private String fragmentShaderCode = "precision mediump float;"
+ "varying vec4 vColor;"
+ "varying vec4 vDiffuse;" // 從頂點著色器傳過來的插值散射光的值,散射光的值依賴頂點。
+ "void main(){"
+ "gl_FragColor = vColor*vDiffuse;" // 原本的顏色乘上散射光強度
+ "}";上面主要的程式碼含義已經新增在註釋裡面了。還有以下幾個地方需要注意
- 頂點著色器中除了MVP矩陣還傳入了M矩陣,原因是顯然的,當光照照在物體上,計演算法線和該頂點和廣元的位置肯定要用進行過基本變換(平移縮放和旋轉)操作後的位置,上面傳入M矩陣目的就在於此。
- 向流量的點積:ab=|a||b|cosa,因此想要計算夾角的餘弦只需要將向量歸一化在計算點積即可。
- 某一個點的法向量,點的法向量定義為該點的切面垂直向外的向量。對於不規則的形狀找其法線的方法是找其臨界點組成的平面的法向量,也可以求其相鄰的面向量的平均法向量。
接著修改頂點和片元著色器後,再在程式碼中增加獲取uMMatrix、uLightLocation的引用以及往著色器傳遞資料的程式碼
muMMatrixHandle = GLES20.glGetUniformLocation(mProgram, "uMMatrix");
muLightLocationHandle = GLES20.glGetUniformLocation(mProgram, "uLightLocation");
...
GLES20.glUniformMatrix4fv(muMMatrixHandle, 1, false, mMatrix, 0);
GLES20.glUniform3f(muLightLocationHandle, 0, 0, 20); // 注意和攝像機位置的設定,否則設定到背面就只能看見一點點內容了。增加了散射光的效果,可以看到效果明顯好了很多,有些地方比較暗,有些地方就是黑的,因為光照沒有照上。因為散射光根據和光源的角度有關,角度越小越亮,這就是自然界的真實現象。

程式碼下載
鏡面光
鏡面光:現實世界中,當光滑表面被照射後會有方向很集中的反射光,這種反射光就是鏡面光,鏡面光除了依賴入射角外,還依賴觀察者(攝像機)的位置,如果攝像機到被照射點的向量不在反射光集中的範圍內,就看不到鏡面光。
其中
鏡面光示意圖
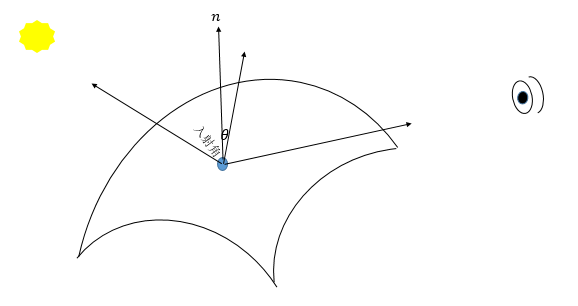
使用鏡面光時,需要將攝像機矩陣傳入頂點著色器中,計算方法只需要按照定義來就可以。
綜合環境光、散射光和鏡面光的模型
gl_FragColor = vColor*vec4(0.5,0.5,0.5,1) + vColor*vDiffuse + vColor*vSpecular