神炎皇

問題描述

神炎皇烏利亞很喜歡數對， 他想找到神奇的數對。
對於一個整數對\((a,b)\)， 若滿足 \(a+b\le n\) 且 \(a+b\) 是 \(ab\) 的因子， 則稱為神奇的數對。 請問這樣的數對共有多少呢？

輸入格式

一行一個整數 \(n\)。

輸出格式

一行一個整數表示答案， 保證不超過 \(64\) 位整數範圍。

資料範圍與約定

對於\(20\%\)的資料 \(n\le 1000\)；

對於\(40\%\)的資料 \(n\le 100000\)；

對於\(60\%\)的資料 \(n\le 10000000\)；

對於\(80\%\)的資料 \(n\le 1000000000000\)；

對於\(100\%\)

說一下考試時候的打表歷程吧（拿了\(40pts\)，如果讓我交答案表了就有\(60pts\)了）

第一個表的列舉\(a+b\)，然後暴力找\(a,b\)

得到了一個沒什麼用的答案表

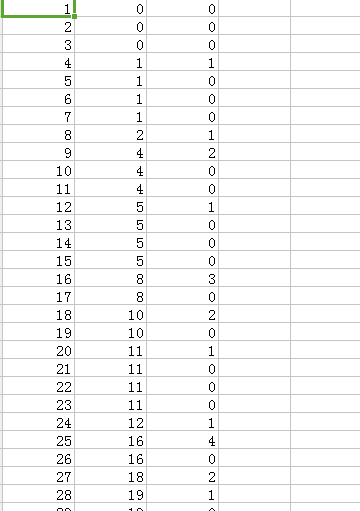
把數對打出來

研究一下發現每個\(a+b\)的貢獻可以這麼算,設\(f(x)\)為\(x=a+b\)的貢獻

則\(f(x)=\sum_{i=1}^x[x|i^2]\)

證明一下也不難，因為\(gcd(i,x)=gcd(x-i.x)\)

發現這樣沒什麼卵用，繼續打表發現

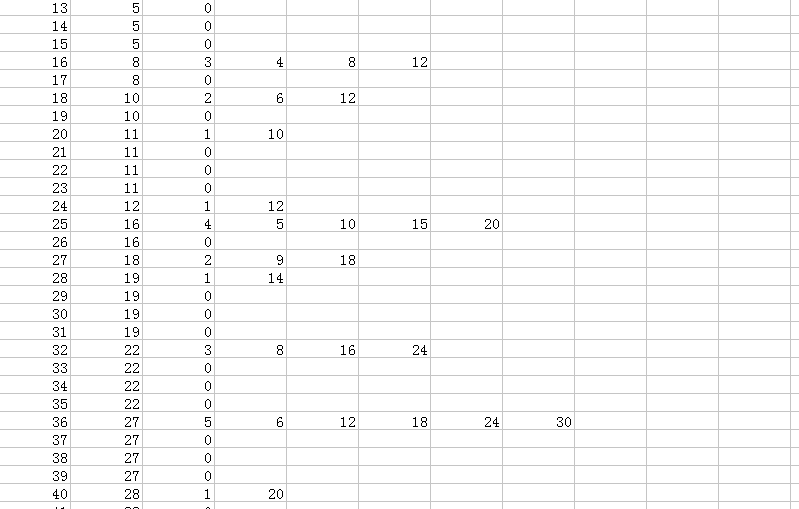
後面的都是第一個的倍數，理解起來也非常簡單，考慮每個數最小滿足的數怎麼搞。

發現就是唯一分解以後，指數除\(2\)

\(x=\prod p_i^{c_i}\)，\(f(x)=\prod p_i^{\lfloor\frac{c_i}{2}\rfloor}-1\)

令\(g(x)=\prod p_i^{\lfloor\frac{c_i}{2}\rfloor}\)

發現\(g(x)\)是積性函式，然而窩並沒想到\(O(n)\)的篩法，只好只拿了\(40pts\)

正解：

設有一對滿足條件的數對\((a,b)\)

設\(d=gcd(a,b),a'=\frac{a}{d},b'=\frac{b}{d}\)

則要滿足條件\((a'+b')d|a'b'd^2\)

即\((a'+b')|a'b'd\)

因為\((a',b')=1\),所以\((a'+b',a')=(a'+b',b')=1\)，所以\((a'+b',a'b')=1\)

則條件為\((a'+b')|d\)

設\(i=a'+b'\)，\(d=ki\)，那麼有\(id=i^2k\le n\)

發現列舉\(i\)只需要到\(\sqrt n\)就可以了，於是列舉\(i\)

對於一個\(i\)，\(k\)的取值個數為\(\lfloor\frac{n}{i^2}\rfloor\)

考慮\(i\)內部的情況，發現是\(\varphi(i)\)，原因很簡單，也是因為\(gcd(i,x)=gcd(i,i-x)\)，考慮一下成對出現就可以了。

那麼答案就為\(\sum_{i=1}^{\sqrt n}\varphi(i)\lfloor\frac{n}{i^2}\rfloor\)

總結：

1. 資料範圍根號提示
2. 想辦法使用\(\varphi ,\mu\)什麼的
3. 胡亂更換列舉項試試（這是很多題的核心了，誰列舉的少好算，我就找誰）
4. 不要忘記打個表

Code:

#include <cstdio>
#define ll long long
const int N=1e7;
int pri[N+10],phi[N+10],ispri[N+10],cnt;
ll ans,n;
void init()
{
    for(int i=2;i<=N;i++)
    {
        if(!ispri[i])
        {
            pri[++cnt]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=cnt&&pri[j]*i<=N;j++)
        {
            ispri[i*pri[j]]=1;
            if(i%pri[j]==0)
            {
                phi[i*pri[j]]=phi[i]*pri[j];
                break;
            }
            else
                phi[i*pri[j]]=phi[i]*(pri[j]-1);
        }
    }
}
int main()
{
    init();
    scanf("%lld",&n);
    for(ll i=1;i*i<=n;i++)
        ans=ans+phi[i]*(n/(i*i));
    printf("%lld\n",ans);
    return 0;
}

2018.11.1