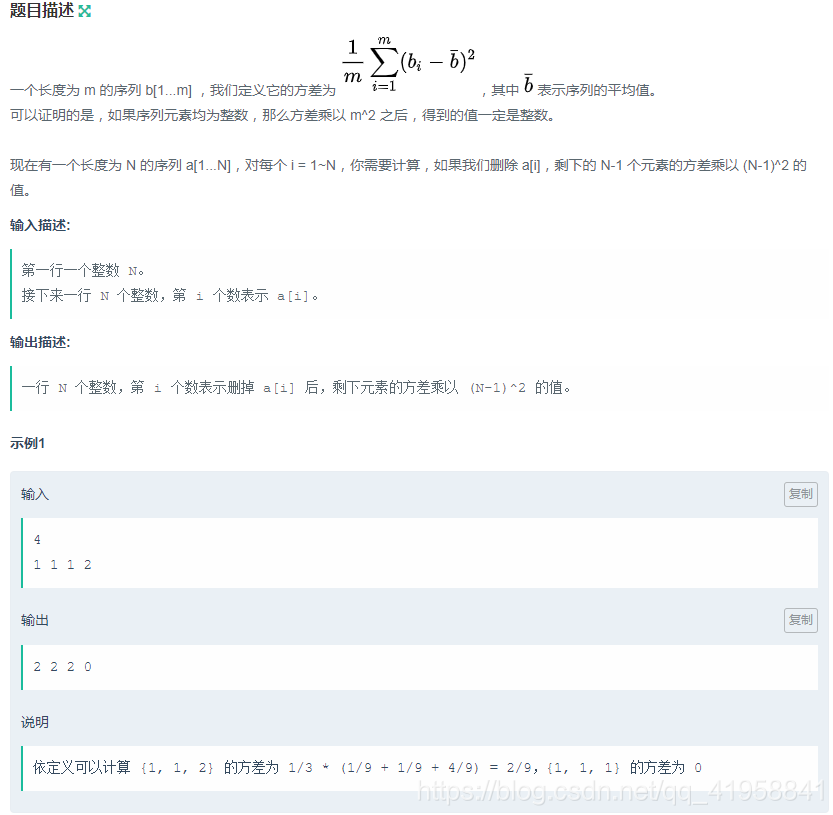
【題解】[牛客網NOIP賽前集訓營-提高組(第二場)]A.方差 字首和
我們把方差公式進行化簡。記
sum1 為每個數的字首和,
sum2 為每個數平方後的字首和
m1i=1∑m(bi−b)2=m1i=1∑m(bi2−2∗bi∗b+b2)=m1(sum2−2∗b∗sum1+m∗b2)=m1(sum2−2∗msum12+msum12)=msum2−m2sum12
於是我們要求的答案為
(n−1)∗(sum2−ai2)−(sum1−ai)2
O(n) 求出字首和後每一步可以
O(1) 求出解
#include<cstdio>
typedef long long ll;
const int N=1e5+10;
int n,a[N];
ll sum2,sum1;
int main()
{
//freopen("in.txt","r",stdin);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),sum1+=a[i],sum2+=a[i]*a[i];
for(int i=1;i<=n;i++)
printf("%lld ",(n-1)*(sum2-a[i]*a[i])-(sum1-a[i])*(sum1-a[i]));
return 0;
}
總結
主考公式化簡
相關推薦
【題解】[牛客網NOIP賽前集訓營-提高組(第二場)]A.方差 字首和
題目連結 我們把方差公式進行化簡。記 s u m
【題解】[牛客網NOIP賽前集訓營-提高組(第二場)]C.集合劃分 狀壓DP
題目連結 看了題解後還是沒寫對,只能去看Komachi大佬咋寫的了。 #include<cstdio> #include<cstring> const int N=18,MX=(1<<18)+5; int n,m,k,ban[N]
【題解】[牛客網NOIP賽前集訓營-提高組(第二場)]B.分糖果 單調棧優化線性DP+容斥原理
題目連結 #include<cstdio> #define re register typedef long long ll; const int N=1e6+10; const int INF=0x3f3f3f3f; const int mod=1e9
【題解】[牛客網NOIP賽前集訓營-提高組(第一場)]C.保護 LCA+線段樹動態開點+線段樹合併
題目連結 ___ #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=2e5+10; int n,m,hd[N],to
【題解】[牛客網NOIP賽前集訓營-提高組(第一場)]B.數數字 線性DP
題目連結 #include<cstdio> #include<cstring> typedef long long ll; #define _rep(i,a,b) for(int i=(a);i<=(b);i++) #define _for(
【題解】[牛客網NOIP賽前集訓營-提高組(第五場)]A.同餘方程 位運算
#include<cstdio> #include<algorithm> using namespace std; typedef long long ll; const ll mod=998244353; ll m,l1,l2,r1,r2; ll
【題解】[牛客網NOIP賽前集訓營-提高組(第四場)]C.滅蟲 線性DP+堆優化
題目連結 #include<cstdio> #include<algorithm> #include<queue> using namespace std; const int N=3e3+10; struct node{ int
【題解】[牛客網NOIP賽前集訓營-提高組(第四場)]B.區間 亂搞
題目連結 #include<cstdio> #include<algorithm> using namespace std; typedef long long ll; const int MAXN=1e7+10; ll a[MAXN]; int
【題解】[牛客網NOIP賽前集訓營-提高組(第四場)]A.動態點分治 模擬
題目連結 #include<cstdio> typedef long long ll; int t,find; ll l,r,k,x; int main() { //freopen("in.txt","r",stdin); scanf("%d",&a
【題解】[牛客網NOIP賽前集訓營-提高組(第三場)]C.急開鎖 博弈論+打表
題目連結 #include<cstdio> typedef long long ll; int t,k,l,r; ll len,f[4000010]; int main() { //freopen("in.txt","r",stdin); scanf("
【題解】[牛客網NOIP賽前集訓營-提高組(第三場)]B.公平競賽 bfs
題目連結 #include<cstdio> #include<cstring> #include<queue> #include<algorithm> using namespace std; inline int rea
【題解】[牛客網NOIP賽前集訓營-提高組(第三場)]A.管道維修 數學期望
題目連結 #include<cstdio> #include<algorithm> #include<cmath> using namespace std; typedef long long ll; #define re regist
【題解】[牛客網NOIP賽前集訓營-提高組(第五場)]B.旅遊 最小生成樹
題目連結 #include<cstdio> #include<algorithm> using namespace std; typedef long long ll; const int N=5e5+10,mod=998244353; inlin
【題解】[牛客網NOIP賽前集訓營-提高組(第五場)]C.串串 組合數
題目連結 #include<cstdio> const int N=4e3+10,mod=1e9+7; int a,b,c,d,fac[N],inv[N],ans; int C(int n,int m) { if(n<0||m<0)return
【題解】[牛客網NOIP賽前集訓營-提高組(第六場)]B.選擇題 期望DP
#include<cstdio> #include<algorithm> using namespace std; const int N=2e3+10; const int mod=998244353; int n,p[N][4],
【題解】[牛客網NOIP賽前集訓營-提高組(第六場)]A.最長路 拓撲排序
題目連結 #include<cstdio> #include<queue> #include<cstring> using namespace std; const int N=1e6+10,mod=998244353; st
【比賽報告】2018.10.30牛客網線上賽[牛客網NOIP賽前集訓營-提高組(第二場)] NOIP練習賽卷二十五
比賽連結 A.方差 字首和 題目連結 我們把方差公式進行化簡。記 s u
牛客網NOIP賽前集訓營-提高組(第一場) A.中位數 [中位數]
A.中位數 思路:二分check是否存在>=mid的中位數,若sum[j]-sum[i]>0 && j-i+1>=len 則一定存在大於等於k的mid #inclu
【比賽報告】2018.10.28牛客網線上賽[牛客網NOIP賽前集訓營-提高組(第一場)] NOIP練習賽卷二十四
比賽連結 A.中位數 二分+字首和 題目連結 構造一個序列 B B B 。每次二分一個
牛客網NOIP賽前集訓營-提高組(第一場)
files desc 有用 做了 關於 有一個 下標 容易 adf 牛客的這場比賽感覺真心不錯!! 打得還是很過癮的。水平也比較適合。 T1:中位數: 題目描述 小N得到了一個非常神奇的序列A。這個序列長度為N,下標從1開始。A的一個子區間對應一個序列,可以由數對[l,