C 圖 鄰接表的基本操作
阿新 • • 發佈:2018-11-01
文章目錄
基本思路
強烈推薦大家看看,同胞寫的,講的特別清楚
圖 – 我的理解就是若干個節點,再加上他們之間的聯絡;這樣就是兩塊內容,一個放節點,一個放他們的關係。
最直觀就是弄一個二維陣列,行列為1的就是連著的,為0就是沒有。

但是太佔空間了,於是就有了這樣的,前面一列就是所有頂點排列,後面每個頂點跟著的就是和這個頂點連著的節點。
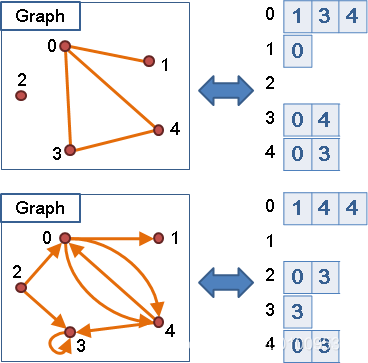
根據這個理解,就可以把鄰接表弄的七七八八了
儲存結構
#define M 100
#define true 1 建立
void creatGraph(GraphLink *g){
int i, j, k;
EdgeNode *p;
printf("輸入頂點數目,邊數和有向?:\n" 列印
void putGragh(GraphLink g){
int i;
//遍歷一遍頂點座標,每個再進去走一次
for (i = 0; i < g->node_num; i++) {
EdgeNode * p = g->adjlist[i].firstedge;
while (p) {
printf("%c->%c ", g->adjlist[i].date, g->adjlist[p->adj_vex_index].date);
p = p->next;
}
printf("\n");
}
}
廣度遍歷
//廣度遍歷
void BFSTraverse(Graph *g)
{
int i;
int tmp;
EdgeNode *p;
//初始化佇列
LinkQueue q;
initQueue(&q);
//防一手不連通的圖
for (i = 0; i < g->node_num; i++) {
if(!visited[i]){
visited[i] = true;
printf("%c ",g->adjlist[i].date);
//佇列插進來一個節點
InsertQueue(&q, i);
//佇列不是空的時候就從佇列裡面操作
while (!isEmpty(&q)) {
//從佇列取一個就得把和他連著的點都填進去
DeleteQueue(&q, &tmp);
//新增和他連著的所有未點亮的點
p = g->adjlist[tmp].firstedge;
while (p) {
if (!visited[p->adj_vex_index]) {
visited[p->adj_vex_index] = true;
printf("%c ",g->adjlist[p->adj_vex_index].date);
InsertQueue(&q, p->adj_vex_index);
}
p = p->next;
}
}
}
}
}
深度遍歷
//得有個陣列記錄一下我走過的點點
int visited[M];
//經典演算法
/*
a| a->b a->d a->c
b| b->c b->g b->a
c| c->b c->a
d| d->a
e| e->f
f| f->e
g| g->b
從頂點數組裡找,找第一個a,然後記錄了a已經點亮了
接著從a連著的點裡往下找,找到了b,b也被點亮
然後再從b裡往下找,找到c,c點亮
從c往下找,找到b,判斷並pass,又找到a並判斷,c連線的點已經都找過了
再回到b,往下找找到g...
就這樣以此類推
用遞迴很巧妙的解決了這個問題,遞迴真屌!!!
*/
void DFS(Graph *g, int i){
visited[i] = true;
printf("%c ",g->adjlist[i].date);
EdgeNode *p = g->adjlist[i].firstedge;
while (p) {
if(visited[p->adj_vex_index] == 0){
DFS(g, p->adj_vex_index);
}
p = p->next;
}
}
//防一手不連通的圖
void DFSTraverse(Graph *g)
{
int i;
for (i = 0; i < g->node_num; i++)
{
if (!visited[i])
DFS(g, i);
}
}
完整程式碼
//
// main.c
// 圖鄰接表
//
// Created by 赫凱 on 2018/10/28.
// Copyright © 2018 赫凱. All rights reserved.
//
#include <stdio.h>
#include <stdlib.h>
#define M 10
#define true 1
#define false 0
////////////
typedef int Elemtype;
typedef struct QNode{
Elemtype data;
struct QNode *next;
}QNode, *QueuePrt;
typedef struct {
QueuePrt front, rear;
}LinkQueue;
//初始化
void initQueue(LinkQueue *q){
q->front = q->rear = (QueuePrt)malloc(sizeof(QNode));
if(!q->front)
exit(0);
q->front->next = NULL;
}
//插入一個節點
void InsertQueue(LinkQueue *q, Elemtype e){
QueuePrt p;
p = (QueuePrt)malloc(sizeof(QNode));
if(p == NULL)
exit(0);
p->data = e;
p->next = NULL;
//插進去
q->rear->next = p;
q->rear = p;
}
//出佇列
void DeleteQueue(LinkQueue *q, Elemtype *e){
QueuePrt p;
if( q->front == q->rear ){
return;
}
p = q->front->next;
*e = p->data;
q->front->next = p->next;
if(q->rear == p)
q->rear = q->front;
free(p);
}
//銷燬一個佇列
void DestroyQueue(LinkQueue *q){
while (q->front) {
q->rear = q->front->next;
free(q->front);
q->front = q->rear;
}
}
//佇列是否為空
int isEmpty(LinkQueue* a)
{
if(a->front == a->rear)
return 1;
return 0;
}
////////////
typedef char Element;
typedef int BOOL;
//鄰接表的節點
typedef struct Node{
int adj_vex_index; //弧頭的下標,也就是被指向的下標
Element data; //權重值
struct Node * next; //邊指標
}EdgeNode;
//頂點節點表
typedef struct vNode{
Element date; //頂點的權值
EdgeNode * firstedge; //頂點下一個是誰?
}VertexNode, Adjlist[M];
//總圖的一些資訊
typedef struct Graph{
Adjlist adjlist; //頂點表
int arc_num; //邊的個數
int node_num; //節點個數
BOOL is_directed; //是不是有向圖
}Graph, *GraphLink;
void creatGraph(GraphLink *g){
int i, j, k;
EdgeNode *p;
printf("輸入頂點數目,邊數和有向?:\n");
scanf("%d %d %d", &(*g)->node_num, &(*g)->arc_num, &(*g)->is_directed);
//安排一下頂點陣列,有幾個走幾個,安排的明明白白
printf("輸入頂點資訊:\n");
for (i = 0; i < (*g)->node_num; i++) {
getchar();
scanf("%c", &(*g)->adjlist[i].date);
(*g)->adjlist[i].firstedge = NULL;
}
printf("輸入邊資訊:\n");
//再安排下邊,想來想去,還是教程給的最簡便,就是我知道邊的兩端是誰就好了
for (k = 0; k < (*g)->arc_num; k++){
//第一個輸入的是弧尾下標,第二個是弧頭下標
// i ----> j
getchar();
scanf("%d %d", &i, &j);
//新建一個節點是必須的
p = (EdgeNode *)malloc(sizeof(EdgeNode));
//弧頭的下標
p->adj_vex_index = j;
//頭插法插進去,插的時候要找到弧尾,那就是頂點陣列的下標i
p->next = (*g)->adjlist[i].firstedge;
(*g)->adjlist[i].firstedge = p;
//如果無向的話得額外在加這一句,畢竟是實對稱矩陣
if(!(*g)->is_directed)
{
// j -----> i
p = (EdgeNode *)malloc(sizeof(EdgeNode));
p->adj_vex_index = i;
p->next = (*g)->adjlist[j].firstedge;
(*g)->adjlist[j].firstedge = p;
}
}
}
void putGragh(GraphLink g){
int i;
//遍歷一遍頂點座標,每個再進去走一次
for (i = 0; i < g->node_num; i++) {
EdgeNode * p = g->adjlist[i].firstedge;
while (p) {
printf("%c->%c ", g->adjlist[i].date, g->adjlist[p->adj_vex_index].date);
p = p->next;
}
printf("\n");
}
}
int visited[M];
//深度遍歷
void DFS(Graph *g, int i){
visited[i] = true;
printf("%c ",g->adjlist[i].date);
EdgeNode *p = g->adjlist[i].firstedge;
while (p) {
if(visited[p->adj_vex_index] == 0){
DFS(g, p->adj_vex_index);
}
p = p->next;
}
}
void DFSTraverse(Graph *g)
{
int i;
for (i = 0; i < g->node_num; i++)
{
if (!visited[i])
DFS(g, i);
}
}
//廣度遍歷
void BFSTraverse(Graph *g)
{
int i;
int tmp;
EdgeNode *p;
//初始化佇列
LinkQueue q;
initQueue(&q);
for (i = 0; i < g->node_num; i++) {
if(!visited[i]){
visited[i] = true;
printf("%c ",g->adjlist[i].date);
//佇列插進來一個節點
InsertQueue(&q, i);
//佇列不是空的時候就從佇列裡面操作
while (!isEmpty(&q)) {
//從佇列取一個就得把和他連著的點都填進去
DeleteQueue(&q, &tmp);
//新增和他連著的所有未點亮的點
p = g->adjlist[tmp].firstedge;
while (p) {
if (!visited[p->adj_vex_index]) {
visited[p->adj_vex_index] = true;
printf("%c ",g->adjlist[p->adj_vex_index].date);
InsertQueue(&q, p->adj_vex_index);
}
p = p->next;
}
}
}
}
}
int main(int argc, const char * argv[]) {
// insert code here...
GraphLink g = (Graph *)malloc(sizeof(Graph));
//數目:7 6 0
//頂點資訊:a b c d e f g
//邊的資訊:0 2 0 3 0 1 4 5 1 6 1 2
creatGraph(&g);
putGragh(g);
int i;
for (i = 0; i < M; i++) {
visited[i] = false;
}
printf("深度優先遍歷:");
DFSTraverse(g);
for (i = 0; i < M; i++) {
visited[i] = false;
}
printf("廣度優先遍歷:");
BFSTraverse(g
