查詢

符號表

最主要的目的是將一個鍵合一個值聯絡起來。用例能夠將一個鍵值對插入符號表並希望在之後能夠從符號表的所有鍵值對中按照鍵直接找到對應的值，即以鍵值對為單元的資料結構。

無序連結串列順序查詢

效能：N方

有序陣列二分查詢

程式碼

public int rank(Key key){
    int lo = 0,hi = N-1;
    while(lo <= hi){
        int mid = lo + (hi - lo)/2;
        int cmp = key.compareTo(keys[mid]);
        if
 
(cmp < 0) hi = mid - 1;
        else if(cmp > 0) lo = mid + 1;
        else return mid;
    }
    return -1;
}

效能：在N個鍵的有序陣列中進行二分法查詢最多需要(lgN+1)次比較(無論是否成功)

二叉查詢樹

定義：

一個二叉查詢樹(BST)是一顆二叉樹，其中每個節點都含有一個Comparable的鍵(以及相關聯的值)，且每個結點的鍵都大於其左子樹中的任意節點的鍵而小於右子樹的任意節點的鍵。

基本實現

get()查詢,put()插入，
節點結構：鍵值，左連線，右連結，計數器

分析

使用二叉查詢樹的演算法的執行時間取決於樹的形狀。在由N個隨機鍵構成的二叉樹中，查詢命中平均所需的比較次數為~2lnN(約為1.39lgN)

有序性相關操作

1. 查詢最大最小鍵
2. 向上向下取整（尋找大於給定值的最小鍵，小於給定值的最大鍵）
3. 選擇（找到排名為k的鍵）
4. 排名（找到給定鍵的排名k）
5. 刪除（刪除最大最小鍵，刪除任意鍵）
   刪除任意鍵的演算法：使用前繼或後繼節點替換空出的位置。
6. 範圍查詢
   中序遍歷：
   按順序列印：列印左子樹->列印跟節點->列印右子樹

private void print(Node x){
    if
 
(x == null) return;
    print(x.left);
    System.out.println(x.key);
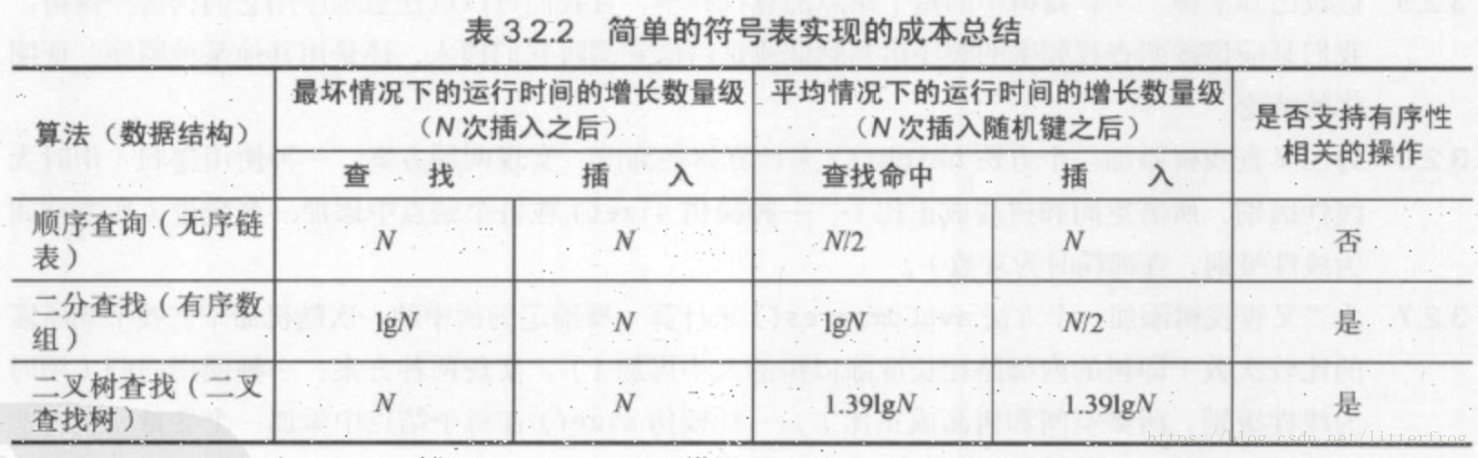
    print(x.right);
}

簡單符號表成本總結

缺點

普通二叉查詢樹的高度跟鍵的插入順序有關，對於足夠大的N，這個值趨近於2.99lgN。但我們仍然無法保證二叉查詢樹的效能。而平衡二叉樹就是解決了這一問題。

平衡查詢樹

2-3查詢樹

定義

一顆2-3查詢樹或是一顆空樹，或由以下節點組成：

• 2-節點：一個鍵兩連結
• 3-節點：兩個鍵三連結

插入操作

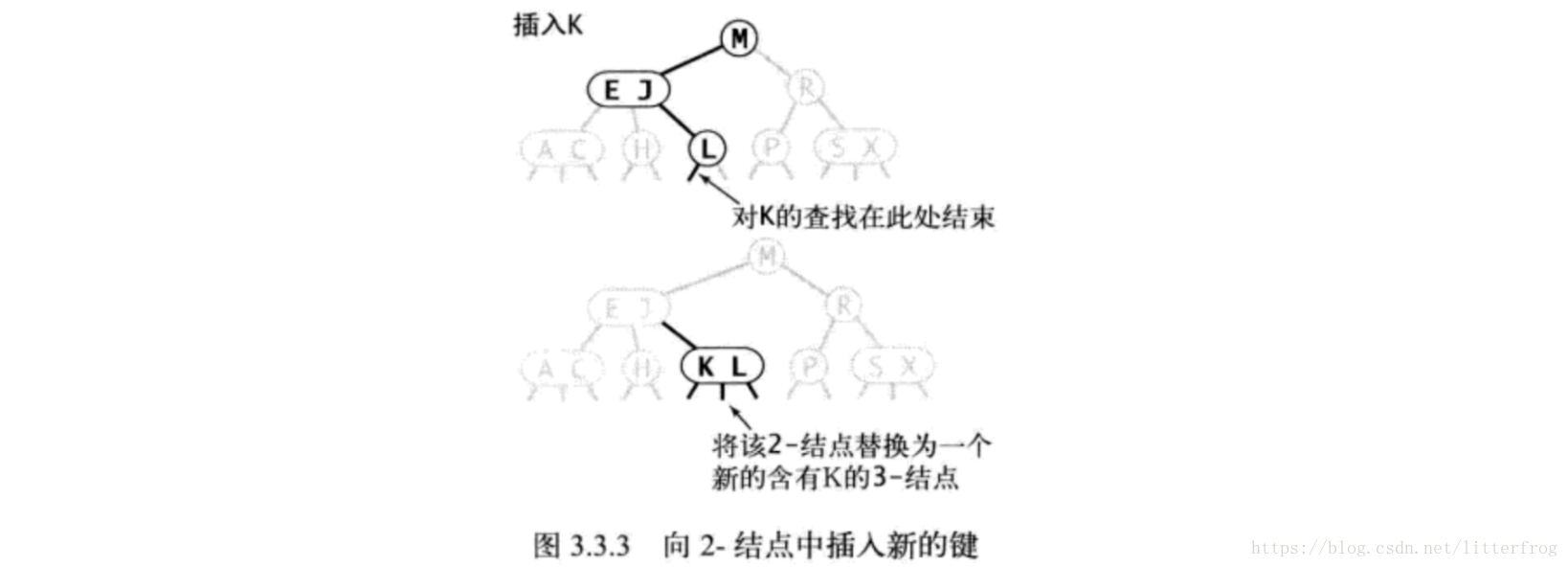
1. 向2-結點插入新鍵：先進行一次未命中查詢，將2-葉子結點替換成3-葉子結點。圖3.3.3
   
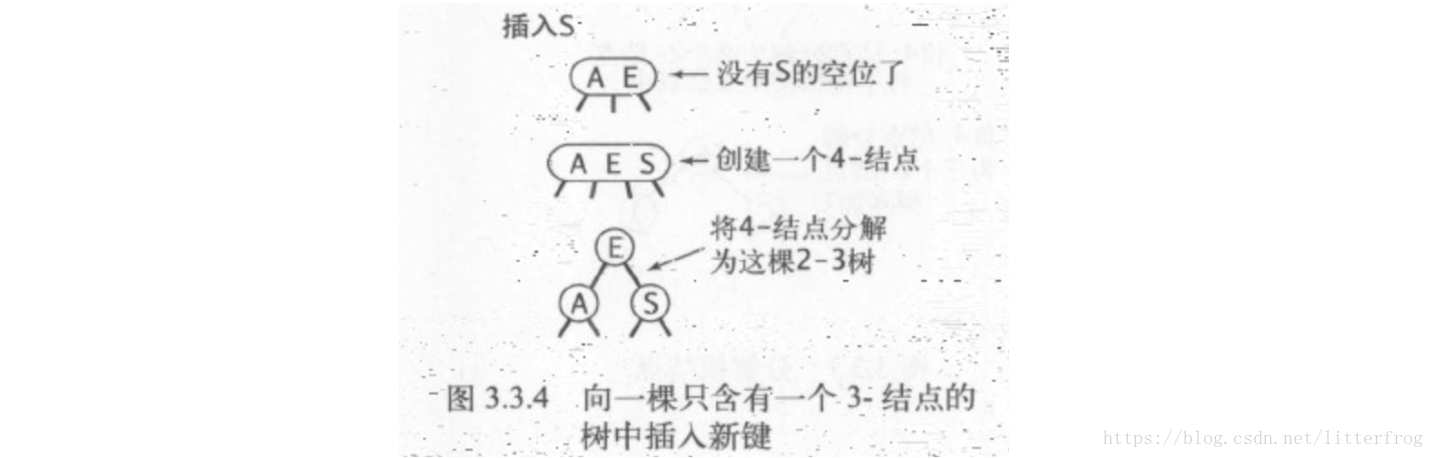
2. 向一棵只含有一個3-結點的樹中插入新鍵：先臨時將新鍵插入這個3-結點使之成為4-結點，再將4-結點的中間鍵上移，變換成3個2-結點，樹的高度+1。圖3.3.4
   
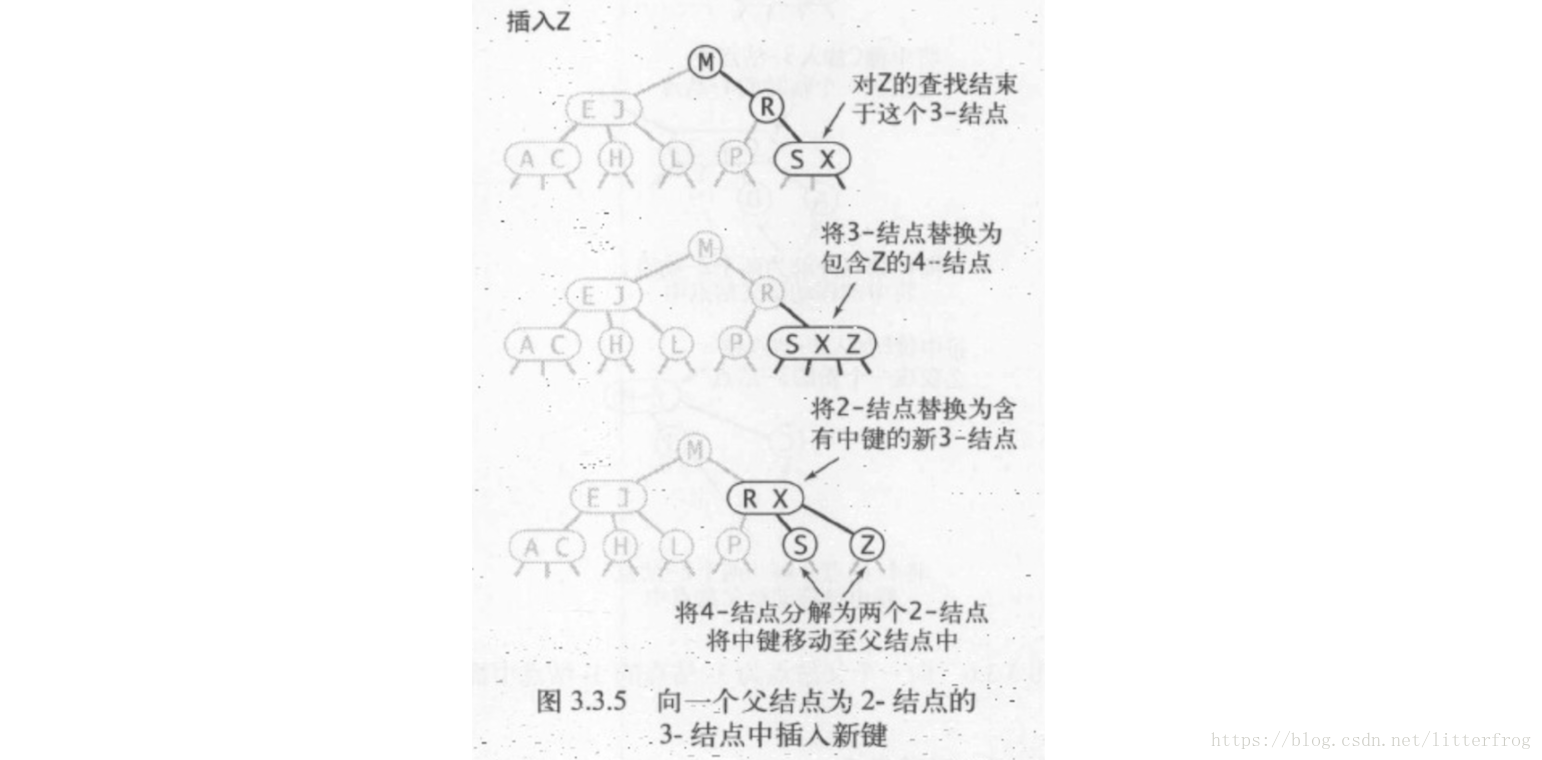
3. 向一個父節點為2-結點的3-結點中插入新鍵：跟2）中一樣先生成一個臨時的4-結點，將4-結點分解，但此時我們不會為中鍵建立一個新結點，而是將其移動至原來的父結點中。圖3.3.5
   
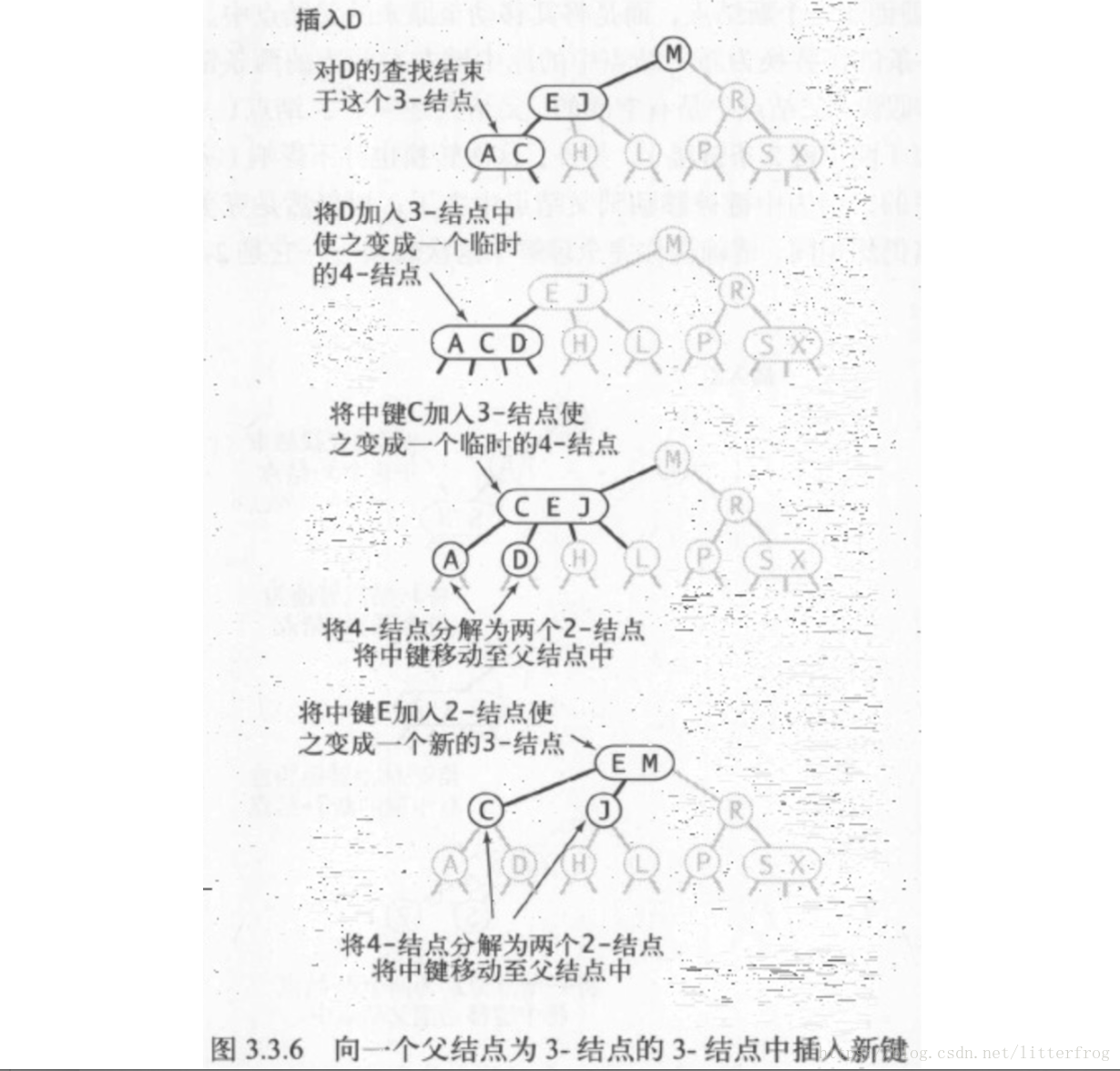
4. 向一個父節點為3-結點的3-結點中插入新鍵：遞迴重複4-結點的拆分。圖3.3.6
   
5. 2-3樹的6種變換情況：圖3.3.8
   

注意：以上變換都不會影響樹的完美平衡性，因為除了根結點的4-分解情況之外，樹的高度都不會增加，根結點的4-分解會使樹的整體高度加1。

效能

在一棵大小為N的2-3樹中，查詢和插入操作訪問的結點必然不超過lgN（N個結點的2-3樹的高度在log(3)N=(lgN/lg3)和lgN之間。）
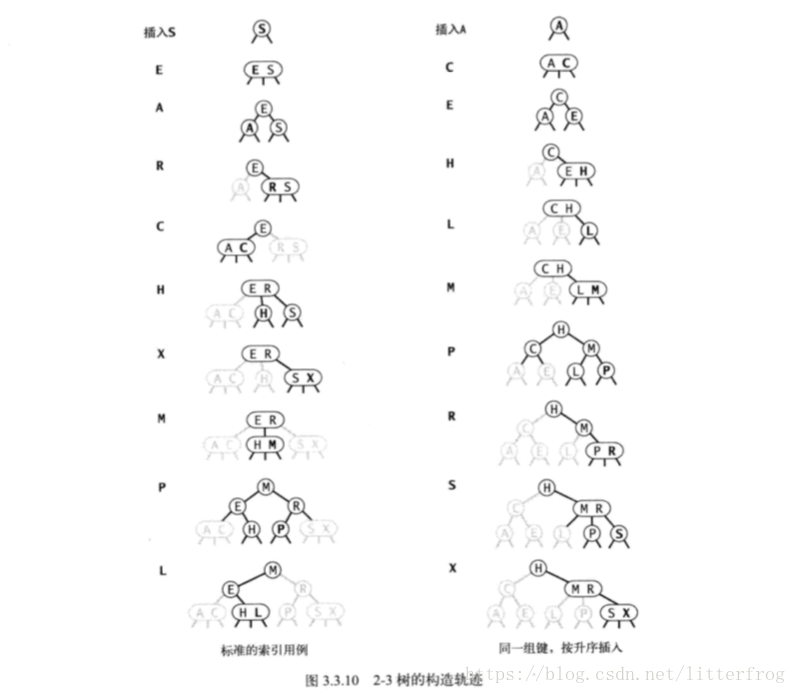
連續插入10個元素2-3樹的生長情況：圖3.3.10

2-3樹缺點

2-，3-結點的變換操作麻煩，需要處理的情況比較多，要維護兩種不同的結點，難以把結點做簡化的一致的抽象。
幸運的是你將看到，我們只需要一點點代價就能用一種統一的方式完成所有變換。

紅黑二叉樹

旋轉時，把紅節點的父連結看成一條紅線，紅線上的內側子結點（即紅色左連結的右子結點或紅色右連結的左子結點）可以在紅線上沿著重力的方向自由滑動。

紅黑樹的由來：替換3-結點

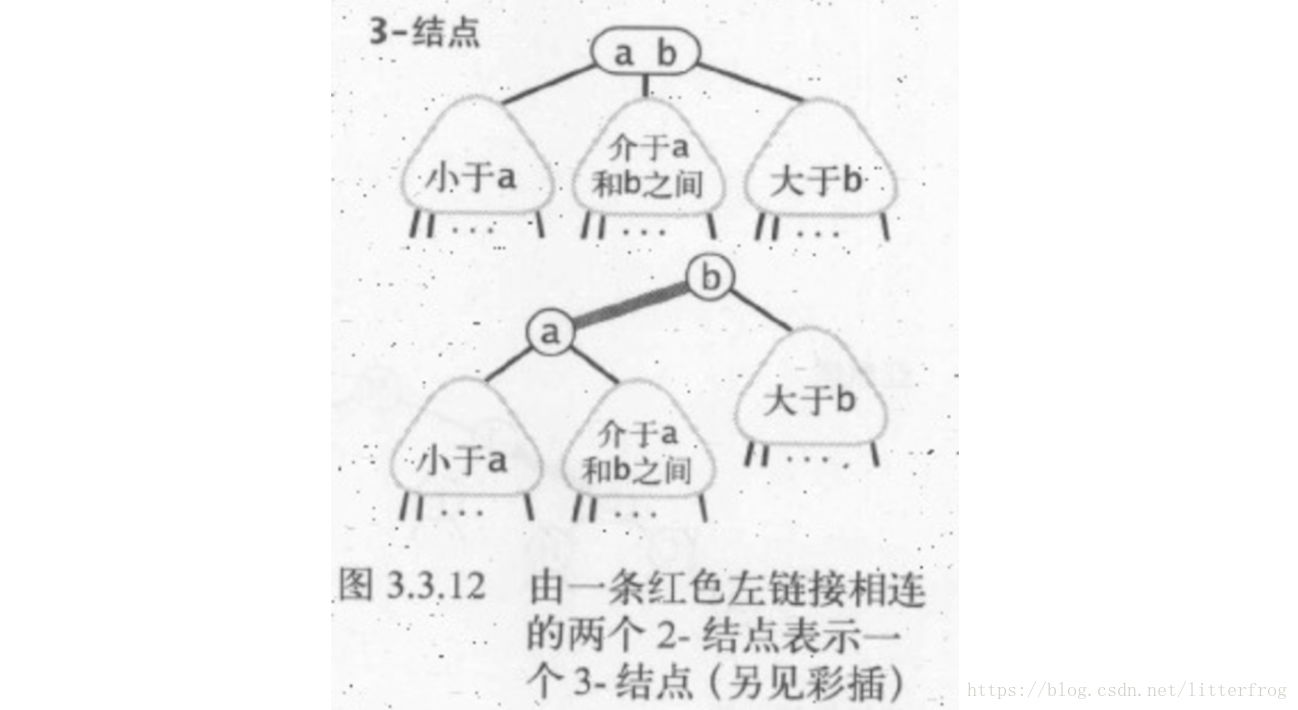
紅黑二叉查詢樹背後的基本思想是用標準的二叉查詢樹（完全由2-結點構成）和一些額外的資訊（替換3-結點）來表示2-3樹。我們將樹中的連結分為兩種型別：紅連結將兩個2-結點連線起來構成一個3-結點，黑連結則是2-3樹中的普通連結。確切地說，我們將3-結點表示為由一條左斜的紅色連結（兩個2-結點中小的是大的的左子結點）相連的兩個2-結點，如下圖3.3.12。我們將用這種方式表示2-3樹的二叉查詢樹成為紅黑二叉查詢樹。

等價定義

紅黑樹的另一種定義是含有紅黑連結並滿足下列條件的二叉查詢樹：

1. 紅連結均為左連結
2. 沒有任何一個結點同時和兩條紅連結相連
3. 該樹是完美黑平衡的，即任意空連結到根結點的路徑上的黑連結數量相同。

與2-3樹對應關係

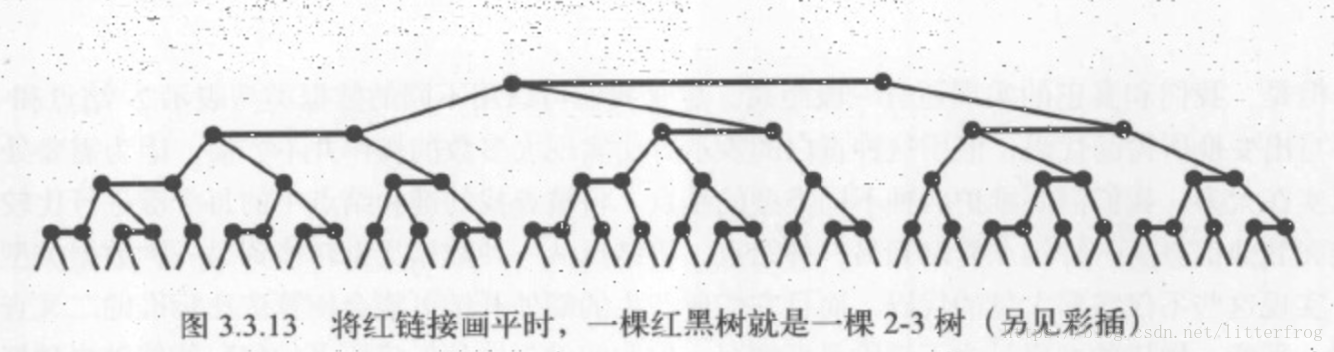
如果將一棵紅黑樹中的紅連結畫平，那麼所有的空連結到根結點的距離都將是相同的。如果我們將由紅連結相連的節點合併，得到的就是一棵2-3樹。圖3.3.13

顏色表示

方便起見，因為每個結點都只會有一條指向自己的連結（從它的父節點指向它），我們將連結的顏色儲存在表示結點的Node資料型別的red成員中。具體見程式碼

public class Node<Key extends Comparable<Key>,Value>{
    Key key;
    Value value;
    Node<Key,Value> left,right;
    int N;
    boolean red;

    public Node(Key key,Value value,int N,boolean red){
        this.key = key;
        this.value = value;
        this.N = N;
        this.red = red;
    }

    private boolean isRed(Node x){
        if(x == null){
            return false;
        }
        return x.red;
    }
}

旋轉

修復紅黑樹，使得紅黑樹中不存在紅色右連結或兩條連續的紅連結。

左旋

將紅色的右連結轉化為紅色的左連結，如圖3.3.16

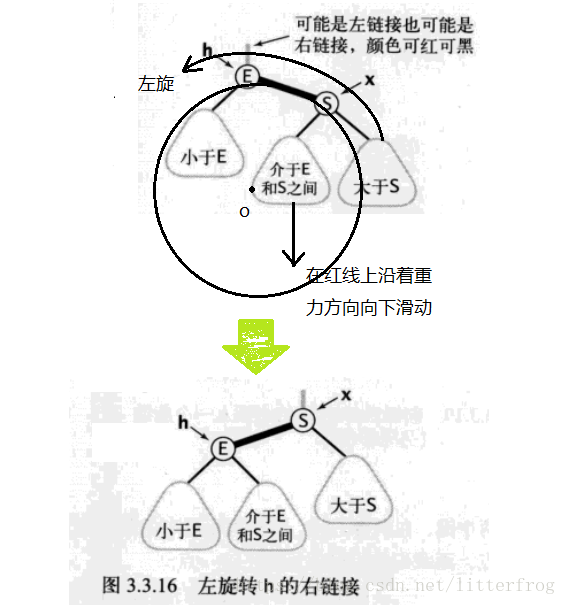
程式碼

Node rotateLeft(Node h){
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = true;
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}

右旋

將紅色的左連結轉化為紅色的右連結，程式碼與左旋完全相同，只要將left換成right即可。如圖3.3.17

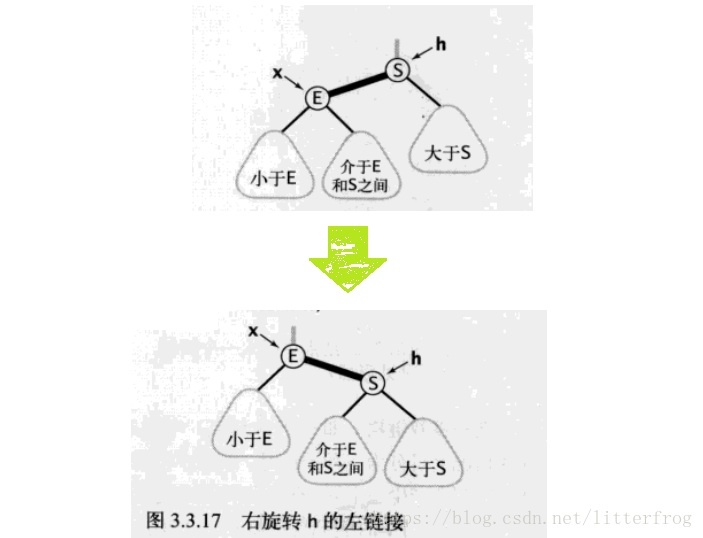
程式碼

Node rotateRight(Node h){
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = true;
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}

插入結點

在插入新的鍵時，我們可以使用旋轉操作幫助我們保證2-3樹和紅黑樹之間的一一對應關係，因為旋轉操作可以保持紅黑樹的兩個重要性質：有序性和完美平衡性。也就是說，我們在紅黑樹中進行旋轉時無需為樹的有序性或者完美平衡性擔心。下面我們來看看應該如何使用旋轉操作來保持紅黑樹的另外兩個重要性質：不存在兩條連續的紅連結和不存在紅色的右連結。我們先用一些簡單的情況熱熱身。

1.向樹底部的2-結點插入新鍵

一棵只含有一個鍵的紅黑樹只含有一個2-結點。插入另一個鍵之後，我們馬上就需要將他們旋轉。如果新鍵小於老鍵，我們只需要新增一個紅色的節點即可，新的紅黑樹和單個3-結點完全等價。如果新鍵大於老鍵，那麼新增的紅色節點將會產生一條紅色的右連結。我們需要使用parent = rotateLeft(parent);來將其旋轉為紅色左連結並修正根結點的連結，插入才算完成。兩種情況均把一個2-結點轉換為一個3-結點，樹的黑連結高度不變，如圖3.3.18和3.3.19

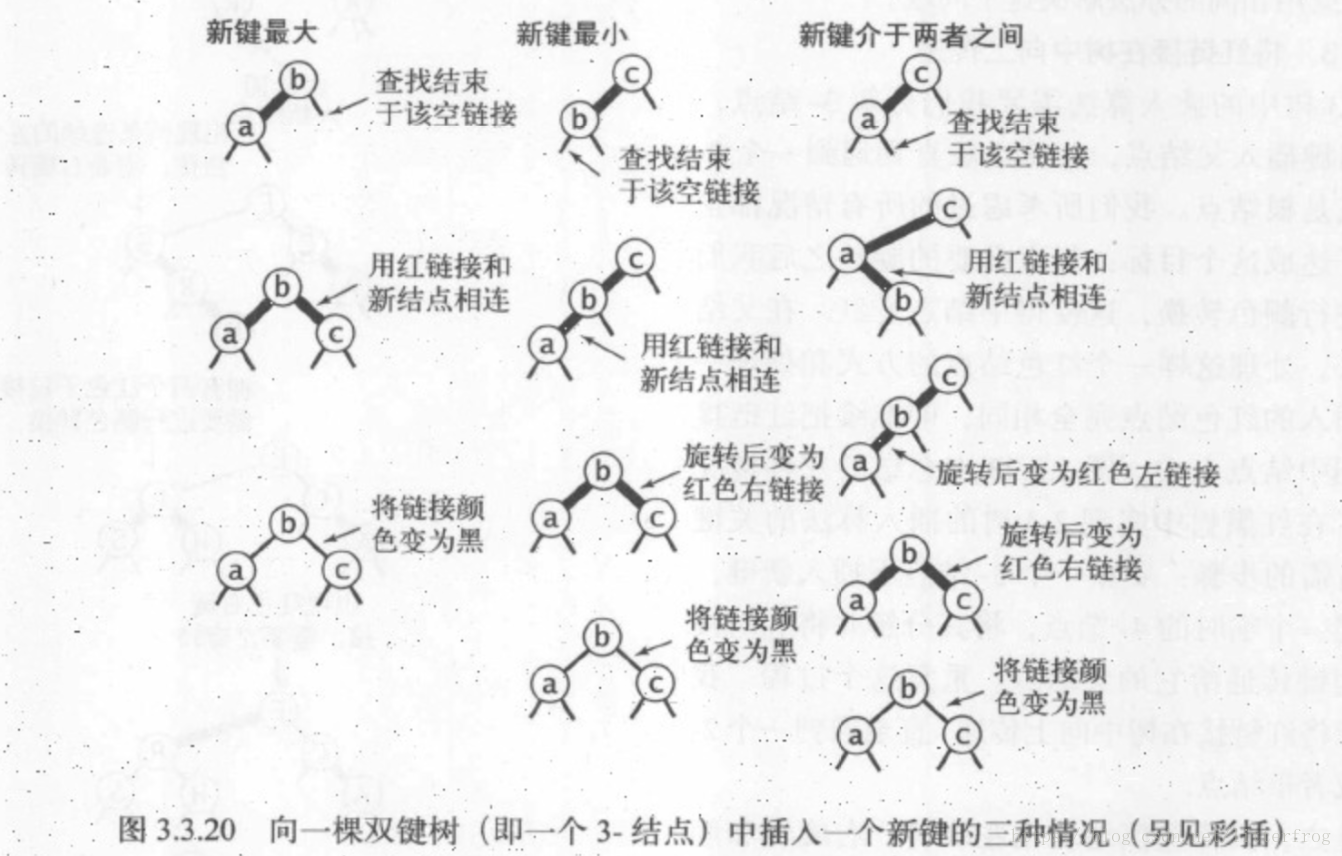
2.向一棵雙鍵樹（即一個3-結點）中插入新鍵

這種情況又可分為三種子情況：新鍵小於樹中的兩個鍵，在兩者之間，或是大於樹中的兩個鍵。每種情況中都會產生一個同時連結到兩條紅連結的結點，而我們的目標就是修正這一點。

1. 三者中最簡單的情況是新鍵大於原樹中的兩個鍵，因此它被連結到3-結點的右連結。此時樹是平衡的，根結點為中間大小的鍵，它有兩條紅連結分別和較小和較大的結點相連。如果我們將兩條連結的顏色都由紅變黑，那麼我們就得到了一棵由三個結點組成，高為2的平衡樹。它正好能夠對應一棵2-3樹，如圖3.3.20（左）。其他兩種情況最終也會轉化為這兩種情況。
2. 如果新鍵小於原書中的兩個鍵，它會被連結到最左邊的空連結，這樣就產生了兩條連續的紅連結，如果3.3.20（中）。此時我們只需要將上層的紅連結右旋轉即可得到第一種情況。
3. 如果新鍵介於原書中的兩個鍵之間，這又會產生兩條連續的紅連結，一條紅色左連結接一條紅色右連結，如果3.3.20（右）。此時我們只需要將下層的紅連結左旋即可看得到第二種情況。
   

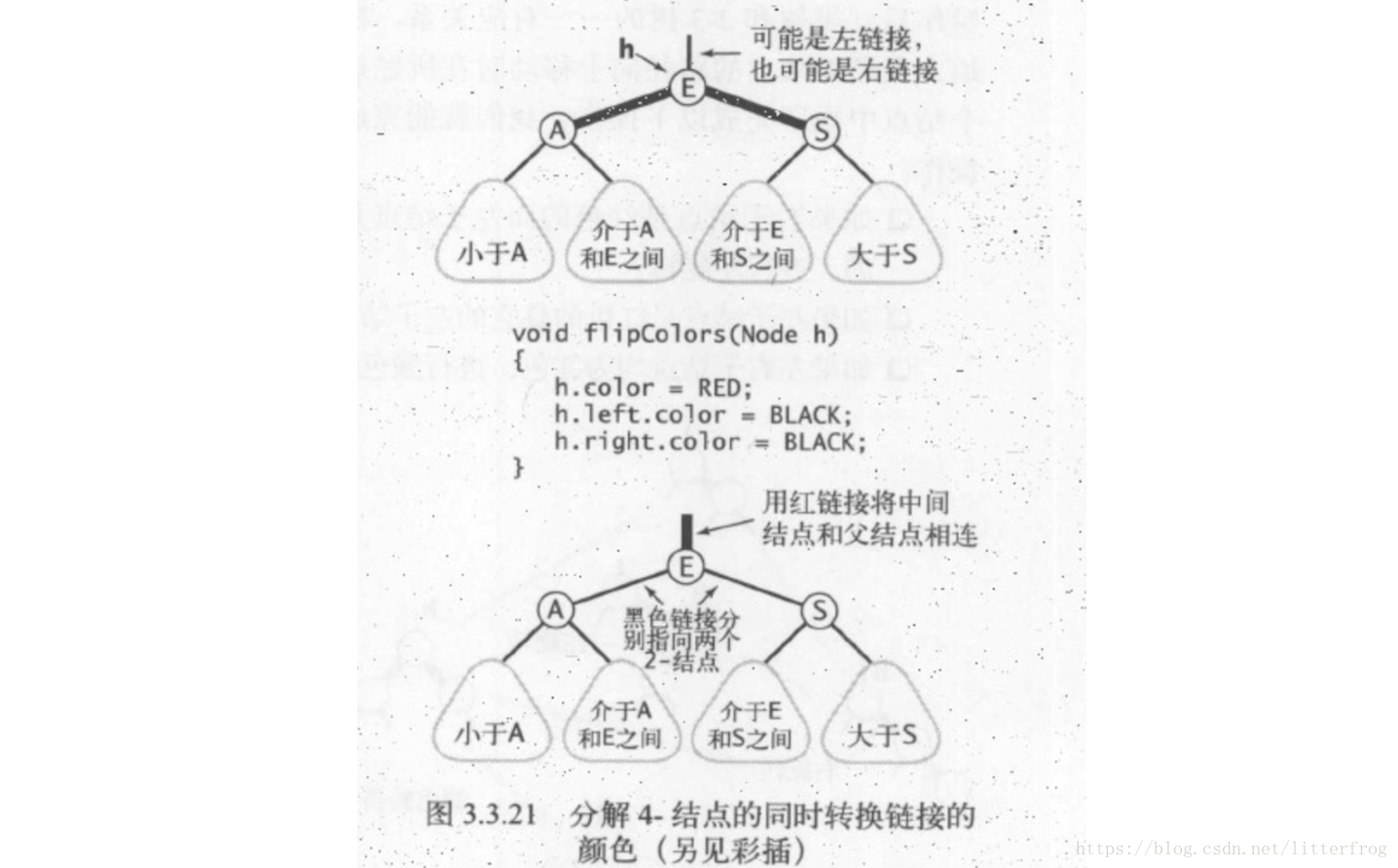
3.顏色轉換

如圖3.3.21，我們專門用一個方法flipColors()來轉換一個結點的兩個紅色字結點的顏色。除了將子結點的顏色由紅變黑之外，我們同時還要將父節點的顏色由黑變紅。這項操作最重要的性質在於它和旋轉操作一樣是區域性變換，不會影響整棵樹的黑色平衡性。根據這一點，我們馬上就能在下面完整實現紅黑樹。

4.根結點總是黑色

顏色轉換會使根結點變為紅色，我們在每次插入操作後都會將根結點設為黑色。

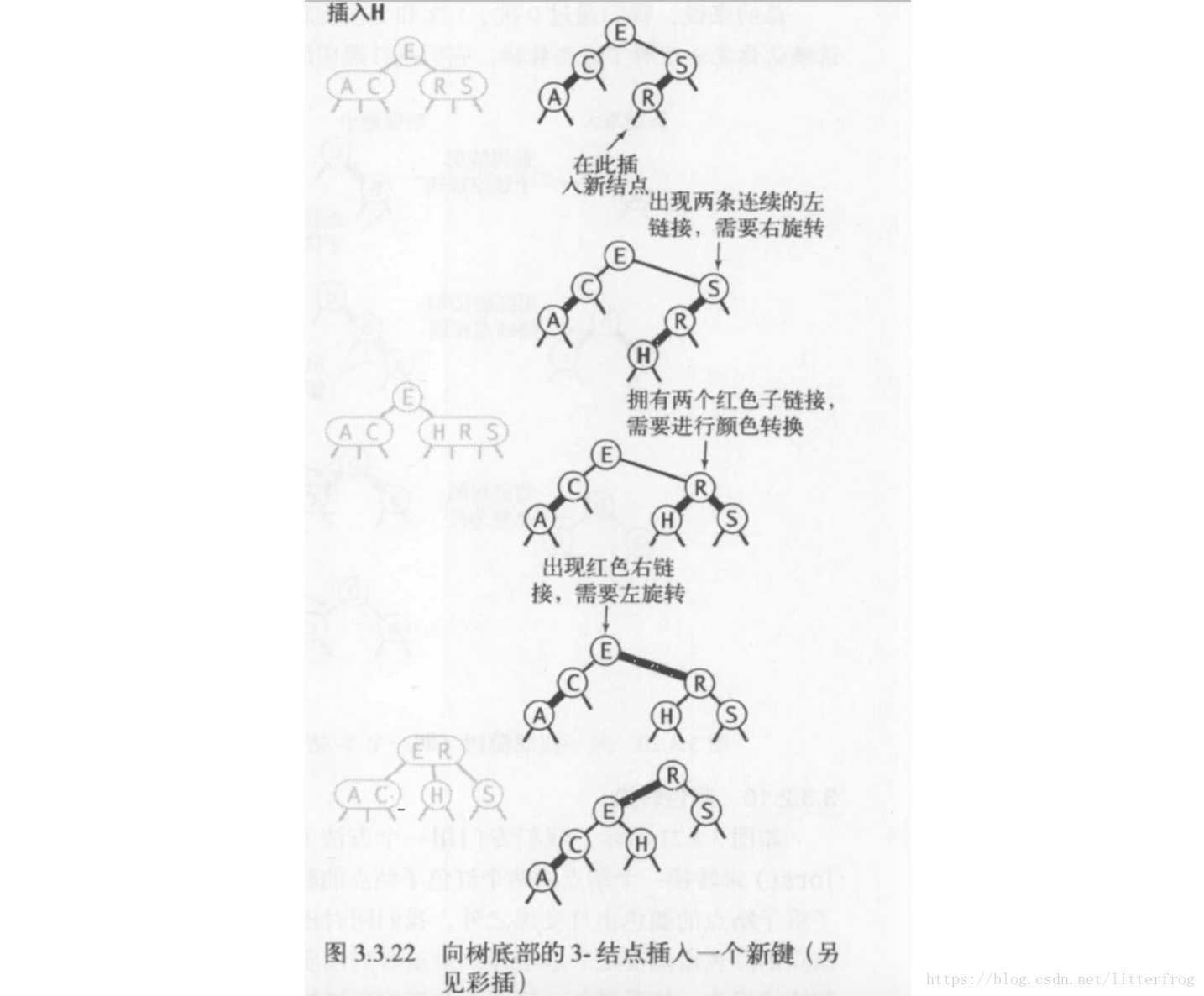
5.向樹底部的3-結點插入新鍵

現在假設我們需要在樹的底部的一個3-結點下加入一個新結點。前面討論過的三種情況都會出現，如圖3.3.22所示。顏色轉換會使指向中結點的連結變紅，相當於將它送入了父結點。這意味著在父結點中繼續插入一個新鍵，我們也會繼續用相同的辦法解決這個問題。

6.將紅連結在樹中向上傳遞

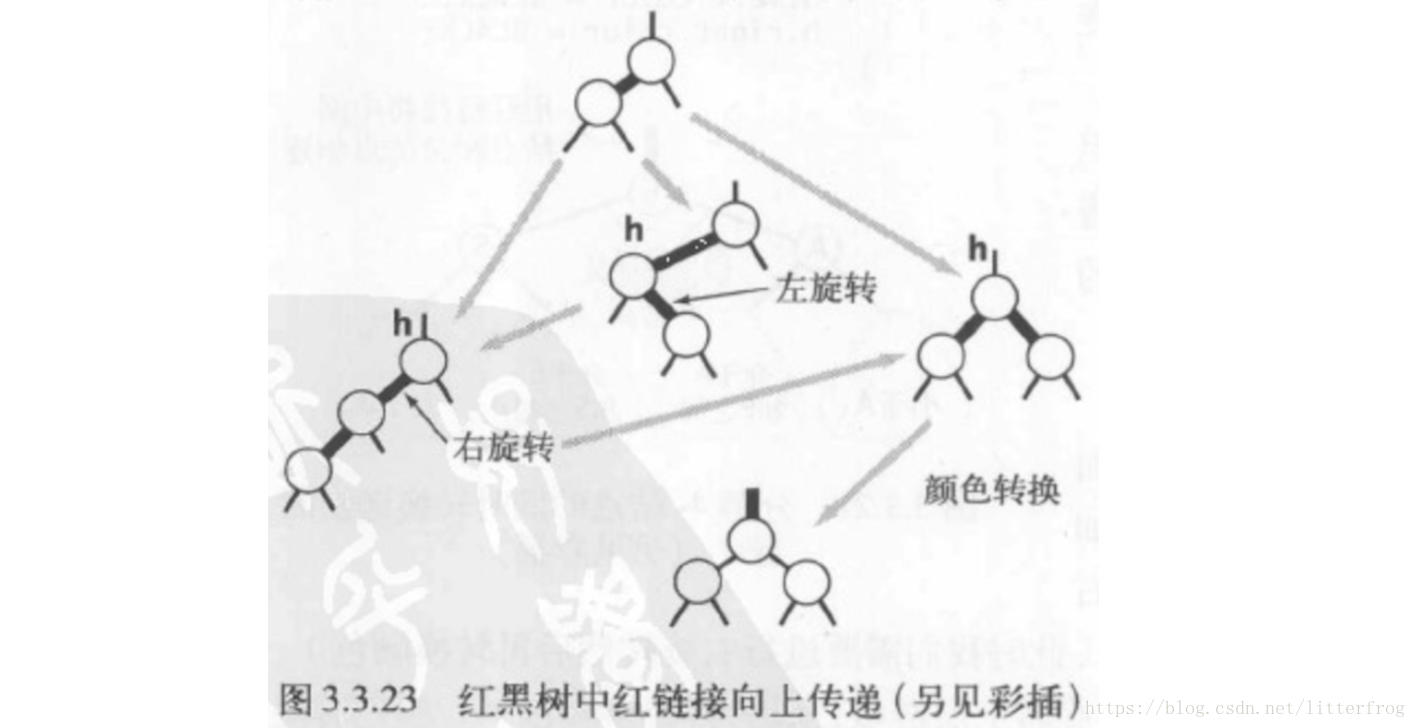
2-3樹中的插入演算法需要我們分解3-結點，將中間鍵插入父結點，如此這般知道遇到一個2-結點或是根結點。總之，只要謹慎地使用左旋，右旋，顏色轉換這三種簡單的操作，我們就能保證插入操作後紅黑樹和2-3樹的一一對應關係。在沿著插入點到根結點的路徑向上移動時在所經過的每個結點中順序完成以下操作，我們就能完成插入操作：

1. 如果右子結點是紅色的而左子結點是黑色的，進行左旋轉
2. 如果左子結點是紅色的且她的左子結點也是紅色的，進行右旋
3. 如果左右子結點均為紅色，進行顏色轉換。
   如圖3.3.23
   

實現

從上到下查詢，由下至上進行平衡變換，如下程式碼

public class RedBlackBST{
    private Node root;
    private boolean isRed(Node h);
    private Node rotateLeft(Node h);
    private Node rotateRight(Node h);
    private void flipColors(Node h);

    private int size(Node node);

    public void put(Node freshNode){
        //查詢key，找到則更新其值，否則為它新鍵一個結點
        root = put(root,freshNode);
        root.red = false;
    }
    private Node put(Node h,Node freshNode){
        if(h == null){//標準插入操作，和父結點用紅連結相連
            return new Node(freshNode.key,freshNode.value,1,true);
        }
        int cmp = freshNode.key.compareTo(h.key);
        if(cmp < 0) h.left = put(h.left,freshNode);
        else if(cmp > 0) h.right = put(h.right,freshNode);
        else h.value = freshNode.value;

        if(isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
        if(isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
        if(isRed(h.left) && isRed(h.right)) flipColors(h);

        h.N = size(h.left) + size(h.right) + 1;
        return h;
    }
}

刪除操作

要描述刪除演算法，首先要回到2-3樹。和插入操作一樣，我們也可以定義一系列區域性變換來在刪除一個結點的同時保持樹的完美平衡性。這個過程比插入一個結點更加複雜，因為我們不僅要在（為了刪除一個結點而）構造臨時4-結點時沿著查詢路徑向下進行變換，還要在分解遺留的4-結點時沿著查詢路徑向上進行變換（同插入操作）。

1.自頂向下的2-3-4樹

作為第一輪熱身，我們先學習一個沿著查詢路徑既能向上也能向下進行變換的稍簡單的演算法：2-3-4樹的插入演算法，2-3-4樹中允許存在我們以前見過的4-結點。它的插入演算法沿著查詢路徑向下進行變換是為了保證當前結點不是4-結點（這樣樹底才有空間來插入新的鍵），沿著查詢路徑向上進行變換是為了將之前建立的4-結點配平，如圖3.3.25所示。

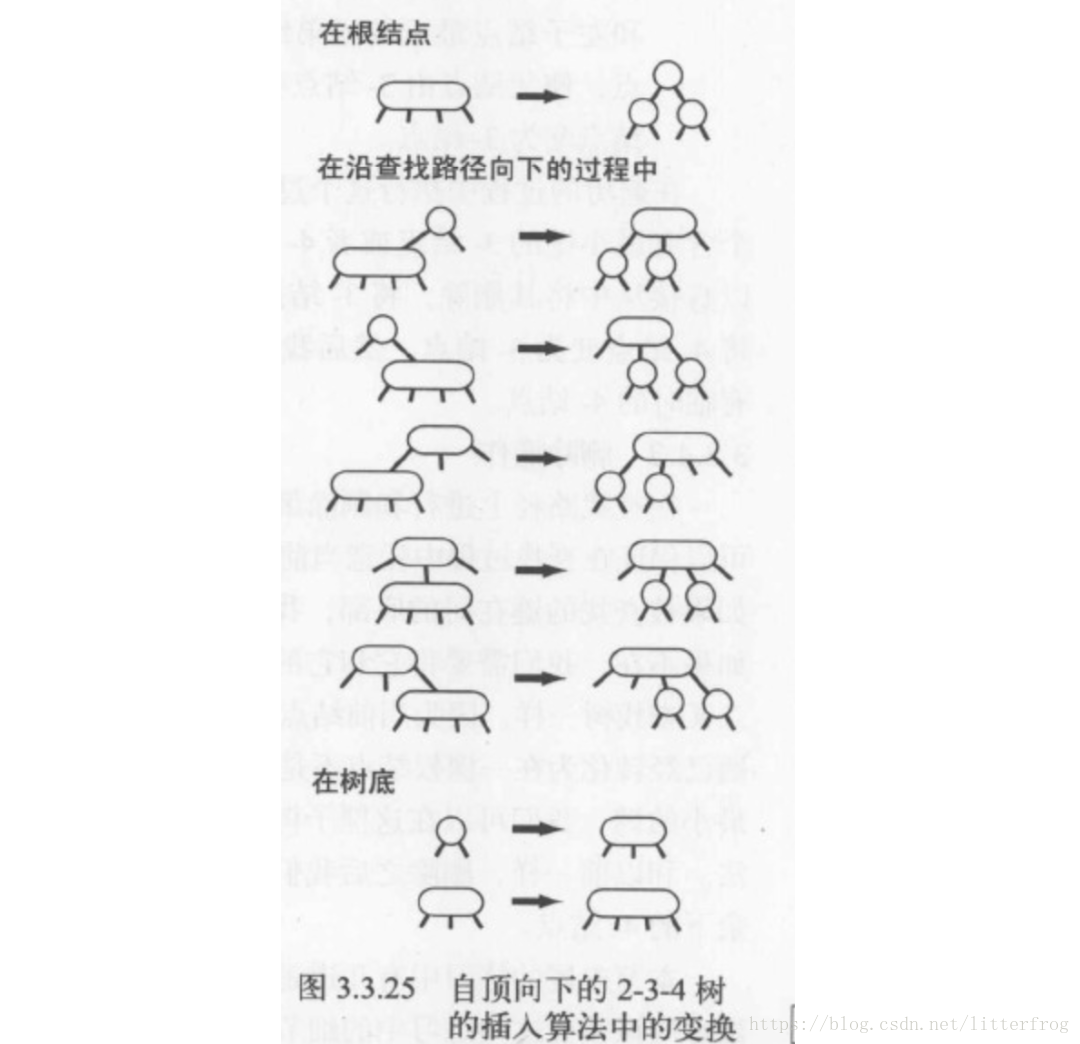
向下的變換和我們在2-3樹中分解4-結點所進行的變換完全相同。如果根結點是4-結點，我們就將它分解成三個2-結點，使得樹高加1。在向下查詢的過程中，如果遇到一個父結點為2-結點的4-結點，我們將4-結點分解為兩個2-結點並將中間鍵傳遞給他的父結點，使得父結點變為一個3-結點；如果遇到一個父結點為3-結點的4-結點，我們將4-結點分解為兩個2-結點並將中間鍵傳遞給它的父結點，使得父結點變為一個4-結點；我們不必擔心會遇到父結點為4-結點的4-結點，因為插入演算法本身就保證了這種情況不會出現。到達樹的底部之後，我們也只會遇到2-結點或者3-結點，所以我們可以插入新的鍵。要用紅黑樹實現這個演算法，我們需要：

1. 將4-結點表示為由三個2-結點組成的一顆平衡的子樹，根結點和兩個子結點都用紅連結相連；
2. 在向下的過程中分解所有4-結點並進行顏色轉換；
3. 和插入操作一樣，在向上的過程中用旋轉將4-結點配平。（因為4-結點可以存在，所以可以允許一個結點同時連結兩條紅連結）。
   令人驚訝的是，你只需要移動上面演算法的put()方法中的一行程式碼就能實現2-3-4樹中的插入操作：將colorFlip()語句（及其if語句）移動到遞迴呼叫之前（null測試和比較操作之間）。在多個程序可以同時訪問同一棵樹的應用中這個演算法優於2-3樹。

2.刪除最小鍵

在第二輪熱身中我們要學習2-3樹中刪除最小鍵的操作。我們注意到從樹底部的3-結點中刪除鍵是很簡單的，但2-結點則不然。從2-結點中刪除一個鍵會留下一個空結點，一般我們會將它替換為一個空連結，但這樣會破壞樹的完美平衡。所以我們需要這樣做：為了保證我們不會刪除一個2-結點，我們沿著左連結向下進行變換，確保當前結點不是2-結點（可能是3-結點，也可能是臨時的4-結點）。首先根結點可能有兩種情況。如果根是2-結點且它的兩個子結點都是2-結點，我們可以直接將這三個結點變為一個4-結點；否則我們需要保證根結點的左子結點不是2-結點，如有必要可以從它右側的兄弟結點“借”一個鍵來。以上情況如圖3.3.26所示。

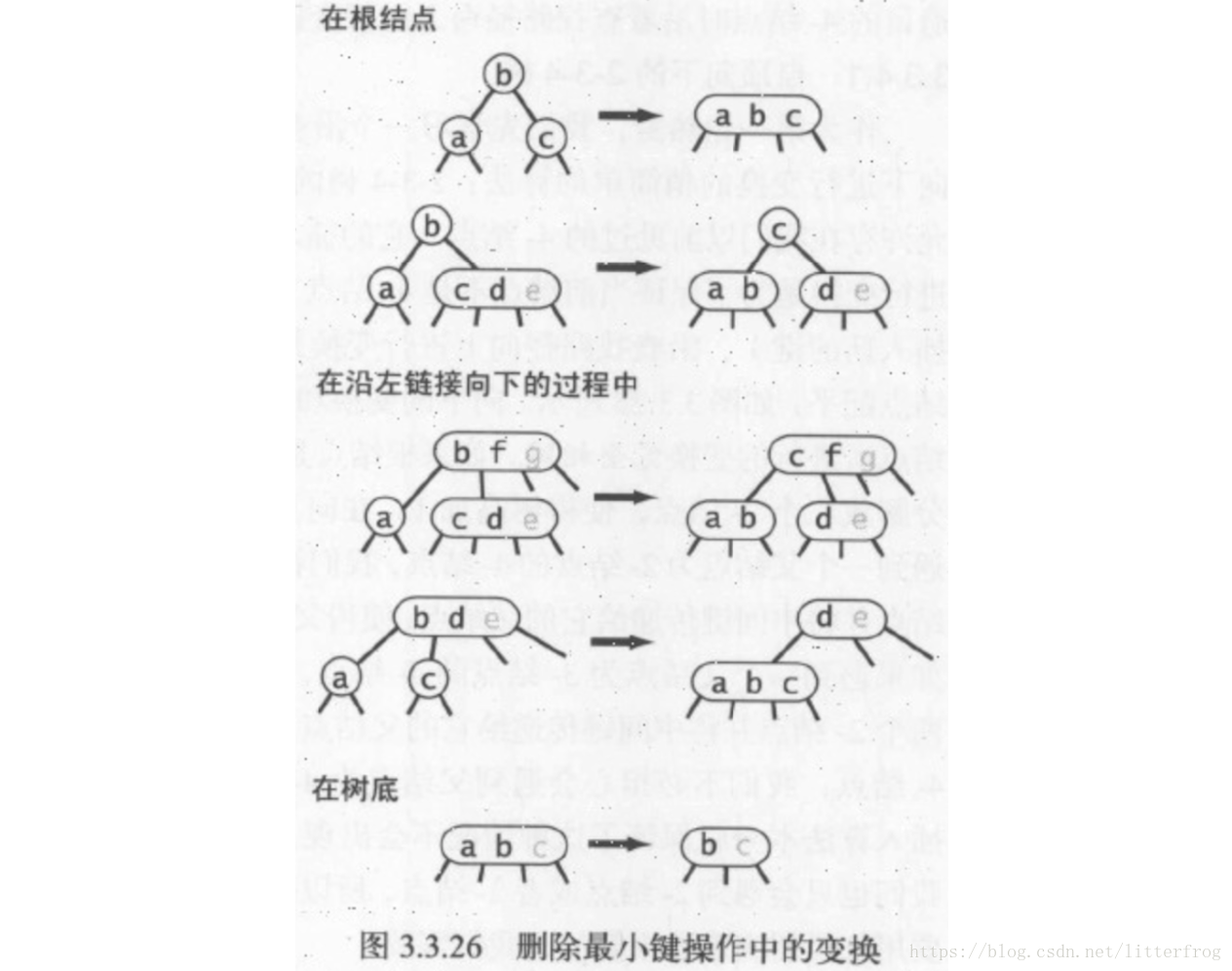
在沿著左連結向下的過程中，保證以下情況之一成立：

1. 如果當前結點的左子結點不是2-結點，完成；
2. 如果當前結點的左子結點是2-結點而它的親兄弟結點不是2-結點，將左子結點的兄弟結點中的一個鍵移動到左子結點中；
3. 如果當前結點的左子結點和它的親兄弟結點都是2-結點，將左子結點，父結點中的最小鍵和左子結點最近的兄弟結點合併為一個4-結點，使父結點由3-結點變為2-結點或由4-結點變為3-結點。

3.刪除操作

在查詢路徑上進行和刪除最小鍵相同的變換同樣可以保證在查詢過程中任意當前結點均不是2-結點。如果被查詢的鍵在樹的底部，我們可以直接刪除它。如果不在，我們需要將它和它的後繼結點交換，就和二叉樹一樣。因為當前結點必然不是2-結點，問題已經轉化為在一顆根結點不是2-結點子樹中刪除最小鍵，我們可以在這個子樹中使用前問所述的演算法。和以前一樣，刪除之後我們需要向上回溯並分解餘下的4-結點。
紅黑樹的性質
重要結論：所有基於紅黑樹的符號表實現都能保證操作的執行時間為對數級別。
一顆大小為N的紅黑樹的高度不會超過2lgN。這個上界是比較保守的，實際上，一顆大小為N的紅黑樹中，根結點到任意結點的平均路徑長度為～1.001lgN。
各種符號表的效能總結