演算法-優先佇列與堆排序
優先佇列
許多應用程式都需要處理有序的元素,但不一定要求他們全部有序,或是不一定要一次就將他們排序。很多情況下我們會收集一些元素,處理當前鍵值最大的元素,然後再收集更多元素,再處理當前鍵值最大的元素,如此這般。
在這種情況下,一個合適的資料結構應該支援兩種操作:刪除最大元素和插入元素。這種資料型別叫做優先佇列。
API
interface MaxPQ<Key extends Comparable<Key>>{
void insert(Key k); //向優先佇列中插入一個元素
Key max(); //返回最大元素 實現
- 有序陣列:在insert中進行排序
- 無序陣列:在delMax時查詢最大元素並刪除。
- 堆:在insert中構造堆,在delMax時需要恢復堆狀態。
對比
堆
定義:當一顆二叉樹的每個節點都大於等於它的兩個子節點時,它被稱為堆有序
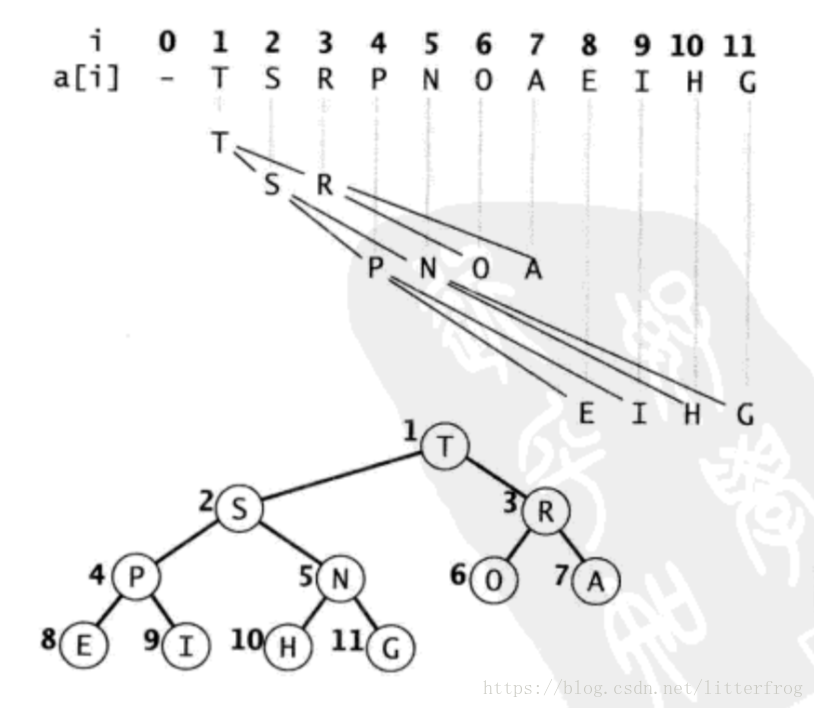
使用陣列儲存堆:在一個堆中,位置k的節點的位置為k/2,而它的兩個子節點的位置則分別為2k和2k+1.這樣在不使用指標的情況下我們也可以通過計算陣列的索引在樹中上下移動:從a[k]向上一層就令k等於k/2,向下一層則令k等於2k或2k+1。如圖
堆的上浮和下沉
使堆維持有序狀態的操作叫做堆有序化。
由下至上的堆有序化(上浮)
如果堆的有序狀態因為某個節點變得比它的父節點更大而被打破,那麼我們需要通過交換它和它的父節點來修復堆。將這樣的節點不斷的向上移動直到遇到一個更大的父節點。
private void swim(int k){
while (k > 1 && less(k/2,k)){
exch(k/2,k);
k = k/2;
}
}由上至下的堆有序化(下沉)
如果堆的有序狀態因為某個節點變得不它的兩個子結點或是其中之一更小而被打破,那麼我們可以通過將它和它的兩個位元組點中的較大者交換來恢復堆。
private void sink(int k){
while (2*k <= N){
int j = 2*k;
if(j < N && less(j,j+1)) j++;
if(!less(k,j)) break;
exch(k,j);
k = j;
}
}基於堆的優先佇列
程式碼:
abstract class MaxPQ<Key extends Comparable<Key>>{
private Key[] pq;
private int N = 0;
public MaxPQ(int maxN){
pq = (Key[]) new Comparable[maxN+1];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
public void insert(Key k){
pq[++N] = k;
swim(N);
}
public Key delMax(){
Key max = pq[1];
exch(1,N--);
pq[N+1] = null;
sink(1);
return max;
}
//實現見前面程式碼
protected abstract boolean less(int i,int j);
protected abstract void exch(int i,int j);
protected abstract void swim(int k);
protected abstract void sink(int k);
}複雜度
對於一個含有N個元素的基於堆的優先佇列,插入元素操作只需要不超過(lgN+1)次比較,刪除最大元素的操作需要不超過2lgN次比較。
堆的拓展
- 多叉堆
- 根據輸入資料長度調整陣列大小
- 索引優先佇列:實現如下
下邊程式碼參考自部落格資料結構實現之最小索引優先佇列
/**
* 使用二叉堆實現的索引最小優先佇列
* class IndexMinPQ是一個支援泛型的索引優先佇列。
* IndexMinPQ支援普通的insert、delete-the-minimum、delete以及change-the-key方法。
* 使用者可以使用佇列中的0到maxN-1號索引執行刪除和修改方法。
* IndexMinPQ支援獲取佇列最小元素,佇列最小元素索引操作。
* IndexMinPQ支援迭代器迭代所有插入的索引號。
*
* IndexMinPQ的實現使用二叉堆。
* The <em>insert</em>, <em>delete-the-minimum</em>, <em>delete</em>,
* <em>change-key</em>, <em>decrease-key</em>, and <em>increase-key</em>
* 操作時間複雜度為O(lgN).
* The <em>is-empty</em>, <em>size</em>, <em>min-index</em>, <em>min-key</em>, and <em>key-of</em>
* operations 時間複雜度為O(1).
* @author xwq
*
* @param <Key>
*/
public class IndexMinPQ <Key extends Comparable<Key>> implements Iterable<Integer> {
private int maxN; //索引優先佇列中元素的最大個數
private int N; //當前索引優先佇列中元素的個數
private int[] pq;//使用一級索引的二叉堆
private int[] qp;//pq的對稱對映 qp[pq[i]] = pq[qp[i]] = i,用於對映key索引對應pq二叉堆中的位置
private Key[] keys; //keys[i] = priority of i
/**
* 初始化索引區間為(0到maxN-1)的空索引優先佇列
* @param capacity
*/
public IndexMinPQ(int capacity) {
if(capacity <= 0)
throw new IllegalArgumentException();
maxN = capacity;
N = 0;
pq = new int[capacity+1];
qp = new int[capacity+1];
keys = (Key[])new Comparable[capacity+1];
//初始每個索引都沒用過
for(int i=0;i<=maxN;i++)
qp[i] = -1;
}
/**
* 如果佇列為空返回true
* @return 如果佇列為空返回true,否則返回false
*/
public boolean isEmpty() {
return N==0;
}
/**
* 佇列的當前元素個數
* @return 佇列的當前元素個數
*/
public int size() {
return N;
}
/**
* 判斷優先佇列是否已存在索引i
* @param i 索引i
* @return 如果索引i之前已插入,返回true,否則false
*/
public boolean contains(int i) {
return qp[i] != -1;
}
/**
* 返回最小值的索引號
* @return 最小值的索引號
*/
public int minIndex() {
if(isEmpty())
throw new NoSuchElementException("IndexMinPQ underflow.");
return pq[1];
}
/**
* 返回優先佇列最小值,即二叉堆根節點
* @return 優先佇列最小值
*/
public Key minKey() {
if(isEmpty())
throw new NoSuchElementException("IndexMinPQ underflow.");
return keys[pq[1]];
}
/**
* 索引i對應優先佇列中的鍵值
* @param i 索引i
* @return 索引i對應的鍵值
*/
public Key keyOf(int i) {
if(!contains(i))
throw new NoSuchElementException("IndexMinPQ has not contains index i");
return keys[i];
}
/**
* 將索引i與鍵值key關聯
* @param i 索引i
* @param key 鍵值key
*/
public void insert(int i,Key key) {
if(i<0 || i>=maxN)
throw new IllegalArgumentException("index i out of boundary.");
if(contains(i))
throw new IllegalArgumentException("index i has allocted");
N++;
qp[i] = N;
pq[N] = i;//pq,qp互為對映
keys[i] = key;
adjustUp(N);
}
/**
* 刪除最小鍵值並返回其對應的索引
* @return 最小鍵值對應的索引
*/
public int delMin() {
if(isEmpty())
throw new NoSuchElementException("IndexMinPQ underflow.");
int min = minIndex();
delete(min);
return min;
}
/**
* 刪除索引i以及其對應的鍵值
* @param i 待刪除的索引i
*/
public void delete(int i){
if(!contains(i))
throw new NoSuchElementException("IndexMinPQ has not contains index i");
int pqi = qp[i];
swap(pqi,N--);
adjustUp(pqi);
adjustDown(pqi);
qp[i] = -1; //刪除
keys[i] = null; //便於垃圾收集
pq[N+1] = -1; //不是必須,但是加上便於理解
}
/**
* 改變與索引i關聯的鍵值
* @param i 待改變鍵值的索引
* @param key 改變後的鍵值
*/
public void changeKey(int i,Key key) {
if(!contains(i))
throw new NoSuchElementException("IndexMinPQ has not contains index i");
if(keys[i].compareTo(key) == 0)
throw new IllegalArgumentException("argument key equpal to the original value.");
if(key.compareTo(keys[i]) > 0)
increaseKey(i,key);//原鍵值增加
else
decreaseKey(i,key);//原鍵值減小
}
/**
* 減小與索引i關聯的鍵值到給定的新鍵值
* @param i 與待減小的鍵值關聯的索引
* @param key 新鍵值
*/
public void decreaseKey(int i,Key key) {
if(!contains(i))
throw new NoSuchElementException("IndexMinPQ has not contains index i");
if(key.compareTo(keys[i]) > 0)
throw new IllegalArgumentException("argument key more than the original value.");
keys[i] = key;
int pqi = qp[i];
adjustUp(pqi);
adjustDown(pqi);
}
/**
* 增加與索引i關聯的鍵值到給定的新鍵值
* @param i 與待增加的鍵值關聯的索引
* @param key 新鍵值
*/
public void increaseKey(int i,Key key) {
if(!contains(i))
throw new NoSuchElementException("IndexMinPQ has not contains index i");
if(key.compareTo(keys[i])<0)
throw new IllegalArgumentException("argument key less than the original value");
keys[i] = key;
int pqi = qp[i];
adjustUp(pqi);
adjustDown(pqi);
}
/***************************************************************************
* General helper functions.
***************************************************************************/
/**
* 交換一級索引值,以及其對稱對映中的值
* @param i 使用一級索引的二叉堆的索引i
* @param j 使用一級索引的二叉堆的索引j
*/
private void swap(int i,int j) {
int t = pq[i]; pq[i] = pq[j]; pq[j] = t;
int qpi = pq[i];
int qpj = pq[j];
qp[qpi] = i;
qp[qpj] = j;
}
/**
* 判斷鍵值的大小關係
* @param i 使用一級索引的二叉堆的索引i
* @param j 使用一級索引的二叉堆的索引j
* @return keys[ki] < keys[kj] 返回true,否則返回false
*/
private boolean less(int i,int j) {
int ki = pq[i];
int kj = pq[j];
return keys[ki].compareTo(keys[kj]) < 0;
}
/***************************************************************************
* Heap helper functions.
***************************************************************************/
/**
* 向下調整最小二叉堆
* @param i 一級索引的二叉堆的索引i,pq陣列的陣列位置
*/
private void adjustDown(int i) {
while(2*i <= N) {
int l = 2*i;
while(l<N && less(l+1,l))
l++;
swap(l,i);
i = l;
}
}
/**
* 向上調整最小二叉堆
* @param i 一級索引的二叉堆的索引i,pq陣列的陣列位置
*/
private void adjustUp(int i) {
while(i>1) {
int p = i/2;
if(less(p,i))
break;
swap(p,i);
i = p;
}
}
@Override
public Iterator<Integer> iterator() {
return new HeapIterator();
}
/***************************************************************************
* Iterators.
***************************************************************************/
/**
* Returns an iterator that iterates over the keys on the
* priority queue in ascending order.
* The iterator doesn't implement <tt>remove()</tt> since it's optional.
*
* @return an iterator that iterates over the keys in ascending order
*/
private class HeapIterator implements Iterator<Integer> {
// create a new pq
IndexMinPQ<Key> copy;
// add all elements to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
copy = new IndexMinPQ<Key>(maxN);
for(int i=1;i<=N;i++) {
int ki = pq[i];
Key key = keys[ki];
copy.insert(ki, key);
}
}
@Override
public boolean hasNext() {
return !copy.isEmpty();
}
@Override
public Integer next() {
if(!hasNext())
throw new NoSuchElementException("IndexMinPQ underflow.");
return copy.delMin();
}
@Override
public void remove() {
throw new UnsupportedOperationException("unsupported remove operation.");
}
}
/**
* Unit tests the <tt>IndexMinPQ</tt> data type.
*/
public static void main(String[] args) {
// insert a bunch of strings
String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" };
IndexMinPQ<String> pq = new IndexMinPQ<String>(strings.length);
for (int i = 0; i < strings.length; i++) {
pq.insert(i, strings[i]);
}
StdOut.print();
// print each key using the iterator
for (Integer i : pq) {
StdOut.println(i + " " + pq.keyOf(i));
}
StdOut.println();
// increase or decrease the key
for (int i = 0; i < strings.length; i++) {
if (StdRandom.uniform() < 0.5)
pq.increaseKey(i, strings[i] + strings[i]);
else
pq.decreaseKey(i, strings[i].substring(0, 1));
}
// delete and print each key
while (!pq.isEmpty()) {
String key = pq.minKey();
int i = pq.delMin();
StdOut.println(i + " " + key);
}
StdOut.println();
// reinsert the same strings
for (int i = 0; i < strings.length; i++) {
pq.insert(i, strings[i]);
}
// delete them in random order
int[] perm = new int[strings.length];
for (int i = 0; i < strings.length; i++)
perm[i] = i;
StdRandom.shuffle(perm);
for (int i = 0; i < perm.length; i++) {
String key = pq.keyOf(perm[i]);
pq.delete(perm[i]);
StdOut.println(perm[i] + " " + key);
}
}
}堆排序
有兩種方式:
- 可以從左到右遍歷陣列,用swim()保證指標左側的所有元素已經是一顆對有序的完全樹
- 可以從右到左使用sink()函式構造最小子堆,然後找到每個已經有序的子堆的父節點構造下一層堆,這樣遞迴的構造直到到達最終的根結點。
sink()的方法效率很高,因為我們事實上只需要遍歷整個陣列的一半即可使整個堆有序。舉個例子假設我們現在要排序16個元素,先將他們填裝到長度為17的數組裡(0位為空)第一次構造的根結點為5-8,第二次的根結點為3-4,第三次的根結點為2,第四次的根結點為1,堆構造完成(這裡的每次指的是構造同一高度的堆)。這時我們呼叫sink()的次數正好是元素個數的一半。然後交換根結點和陣列最右邊未排好序的節點,sink堆,如此直到堆的長度減小為1,整個陣列即有序。
public static void sort(Comparable[] a){
int N = a.length;
for(int k = N/2 ; k >= 1 ; k--)
sink(a,k,N);
while (N > 1){
exch(a,1,N--);
sink(a,1,N);
}
}如圖為堆排序軌跡:
複雜度
用下沉操作由N個元素構造堆只需要少於2N次比較以及少於N次交換。將N個元素排序,堆排序只需少於(2NlgN+2N)次比較(以及一半次樹的交換)。
缺點
在現代系統的許多應用中很少用,因為無法利用快取。陣列元素很少和相鄰的其他元素進行比較,因此快取未命中的次數遠遠高於大多數比較都在相鄰元素間進行的演算法,如快速排序,歸併排序,甚至希爾排序。
優先佇列在java中的實現
見java.util.PriorityQueue