(Java資料結構和演算法)堆---優先佇列、堆排序
阿新 • • 發佈:2018-12-01
堆主要用於實現優先佇列。
利用有序陣列可以實現優先佇列(從小到大或從大到小的陣列),刪除的時間複雜度是O(1),但是插入的時間複雜度是O(N)。用堆實現優先佇列,插入和刪除的時間複雜度都是O(logN)。
簡介
堆是一種完全二叉樹,且每個節點的值都大於等於子節點值(大根堆)。堆的子樹也是完全二叉樹。注意是用陣列來存放堆。
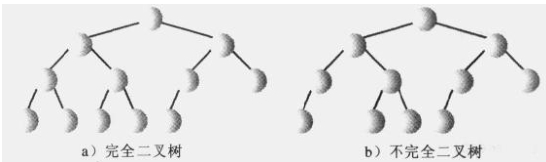
補充下完全二叉樹的規律
(1)n2+1 = n0
設子節點為0、1、2的節點數各是n0,n1,n2,總節點數是n,那麼n = n0 + n1 + n2,同時對一棵樹從上往下看,(假定不是空樹)根節點有1個,依次往下走,有n = 1 + n00 + n1
(2)n = 2*n0 + n1 -1
這個式子從(1)的兩個式子很容易推匯出來。注意完全二叉樹的子節點數是1的節點數目要麼只有1個要麼有0個,即n1的取值是0或1。這就可以把n1消掉,同時,還可以根據n的奇偶性,逼出n1取值到底是0還是1。
(3) 非葉子數是n/2(商)—在後面堆實現的時候trickleDown函式會用到
注意分析這個式子,當n是奇數的時候,n1必定是0,此時n0=(n+1)/2(葉子節點數),當n是偶數的時候,n1必定是1,此時n0=n/2。舉個例子,比如n=8的時候,葉子節點數是n0=8/2=4,n=7的時候,葉子節點數是n0=(7+1)/2=4。這裡有個規律是,無論n是奇數或偶數,不變的是非葉子節點數是n/2(商)。
移除
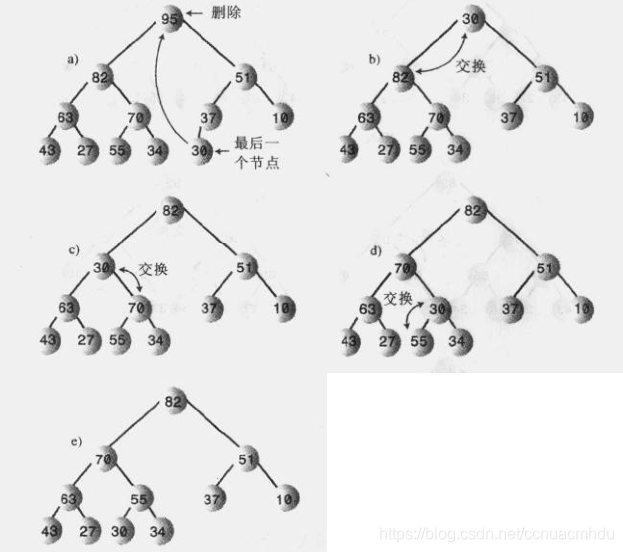
插入

堆實現
class Node{
private int e;
public Node(int e){
this.e = e;
}
public int getE(){
return this.e;
}
public void setE(int e){
this.e = e;
}
}
class Heap{
private Node[] heapArray;
private int maxSize;//容量
private int size;//當前大小
public Heap(int maxSize){
this.maxSize = 
堆排序實現
思路:既然上述大頂堆最大的數永遠在堆的頂部(樹根),那就不斷刪除堆頂,直到樹空,刪除的這個序列就是從大到小排序的!
當然,使用大頂堆也可以實現從小到大排序,只需要把刪除的序列逆序放在數組裡就可以了。
