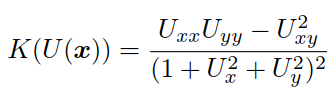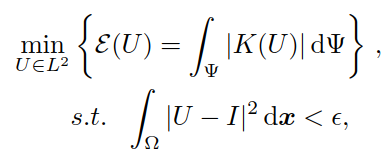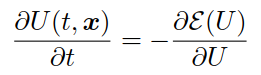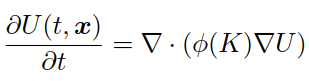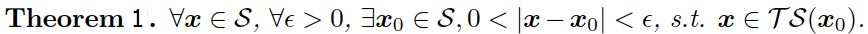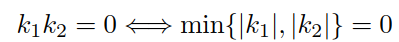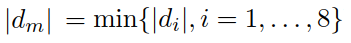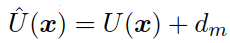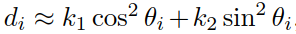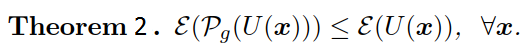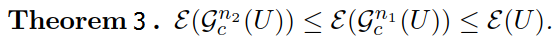前言

大概是兩個月之前開始學習曲率濾波，從一個完全一無所知的狀態開始學習的，包括微分幾何等相關基礎知識也是未曾學習過的，從初學者的角度學習曲率濾波。現在新加坡南陽理工大學任教的龔元浩老師在其2015年博士論文中的第六章給出了理論基礎和實際的應用，包括去噪平滑等，首先針對性的構造了高斯曲率濾波器，給出了詳細的理論基礎，主要是從微分幾何的角度分析了其思想的根本來源，簡言之就是通過某種合理的畫素點投影對映將原始影象3維曲面對映成可展曲面，這裡有個重要的知識點是：最小化平均曲率Mean Curvature會導致極小曲面，最小化高斯曲率Gaussian Curvature會導致可展曲面，可展曲面能夠很好的保留邊緣資訊，因此就涉及了文中所說的ADAP-As Developable As Possible，使曲面儘可能可展。這是最基本的思想，具體的展開學習下面開始，或有理解錯誤的地方，才疏學淺，難免有誤，見諒！

1. 概述

曲率濾波解決的問題其實是求解變分模型，相比之前的擴散方法或梯度下降法等，曲率濾波是從微分幾何的角度最小化相關曲率來實現最小化正則項的方法，作為一個初學者，在真正學習曲率濾波之前，必須要了解的幾個問題，歸納整理一下，也是我在學習過程中，必須要邁過去的坎。

1.1 適定性/病態問題

適定性問題，英文是well-posed problem，病態問題，英文是ill-posed problem，從離散樣本中估計真實影象通常都是病態問題，比如去模糊deblurring，點雲圖像的曲面擬合estimated surface from point image

那麼到底什麼是病態問題呢？

給定影象f(x)，如果x從x增加到x*，則△x=x-x*，其相對誤差是△x/x，f(x*)的相對誤差是（f(x)-f(x*)）/ f(x)，因此相對誤差比是 

|（f(x)-f(x∗) / f(x) ）| / | Δx/x |= C_p

C_p叫做條件數condition number。如果條件數足夠大，相對誤差比也將會很大，這種問題叫病態問題，簡言之就是自變數變化，結果就會出現大的變化，從而導致問題不易求解。

那麼到底如何求解病態問題呢？

病態問題必須要新增正則項或先驗，有關正則項的研究，已經有很多相關論文給出了求解方法，在龔元浩老師的PPT中有下面的總結和描述：

分段常數、分段線性和分段平滑的意思，按我的理解，現在正在看相關的論文，還處在剛開始接觸的階段，可能會有誤，在影象分割問題中，如果將原始影象有意圖的分割成2個區域，那麼每個區域中的畫素值是近似的，在過兩個分割區域的邊界時，畫素值變化是劇烈的，分段常數就是說分割之後的兩個塊區域的函式表示式是分段常數的，不同的區域有不同的值，那麼引申而來的，分段線性就是分割函式是分段線性的，分段平滑也類似的理解。

1.2 微分幾何基礎知識

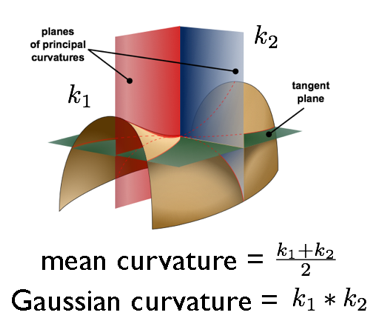
從“曲率濾波”字面意思就能看出，關鍵詞是曲率，曲率的概念在高等數學中簡單的提及到，但是當初的知識點無法支撐我們現在所要研究的領域，因此，簡單的對曲率的學習是必不可少的，本文所及的曲率有兩個重要型別---高斯曲率Gaussian Curvature和平均曲率Mean Curvature，如圖3：

曲面上的一點有一切平面tangent plane，此點處會有各個方向上的曲率，但是必然會有最大主曲率和最小主曲率，k1是最小主曲率，k2是最大主曲率，則平均曲率和高斯曲率的定義如上，具體的微分幾何求解過程可以參考附件中的文件《曲率濾波---微分幾何理論基礎》。

1.3 變分學基礎

在一般高等數學框架中，我們都知道微分的概念，一般的dy=f'(x)dx，但是這不是最基礎的形式，在我整理的文件《曲率濾波---變分學基礎》中， 可以得到這樣的結論：

△y = f'(x) △x + O(△x)

可見，f'(x) △x是函式增量的主要部分，也是其線性部分，即“線性主要部分”，我們把函式增量的線性主要部分f'(x) △x叫做函式的微分，這才是微分的本質。

那麼什麼是變分呢？

變分指的是在泛函理論中的“微分”。

那麼什麼是泛函呢？

把具備某種性質的函式的集合記作D，對於D中的任何函式f(x)，即對任意的f(x)∈D，變數Q都有唯一的值與之相對應，那麼變數Q叫做依賴於f(x)的泛函，記為

Q = Q[f(x)]   或   Q = Q[f]

簡言之就是一般的函式自變數是x，泛函的自變數是函式f(x)，微分是一般函式的自變數x的微增量導致f(x)的變化，變分是泛函中的自變數f(x)的微增量導致的Q的變化。

根據一般函式的微分本質的表達方式，泛函中的微分本質的表達方式也可以類似的描述：

△Q = T[y(x), delta y]  + beta[y(x), delta y] 

這裡，T[y(x), delta y]對delta y而言是線性泛函，即主要部分，而後一項，是相對於max|delta y|的高階無窮小，那麼泛函的變分表示為：

delta Q = T[y(x), delta y]

具體的詳細過程請參考附件《曲率濾波---微分幾何理論基礎》。

2. 高斯曲率濾波器

2.1 序言

根據1.2所述的相關微分幾何知識，我們知道高斯曲率的定義，但是在二維影象中，高斯曲率的定義則是：

在去噪演算法中，用到的變分模型是，總絕對高斯曲率變分模型：

其中，E(U)是高斯曲率能量，e是演化終止閾值，是個很小的數。

很多文獻已經給出了上述問題的求解方法，一般是基於擴散的方法，即diffusion-based algorithm，主要是通過加入偽時間t，直到達到穩定狀態或滿足終止條件：

初始條件U(t=0,x) = I(x)。這個模型已經通過使用幾何流的方法推廣到各向異性擴散方法中（Lee and Seo, 2005）：

具體的演算法可以參考相關文獻，這裡不詳細介紹了。

但是，擴散的方法有兩個問題：

1） 收斂速度慢 收斂速度慢，演化時間複雜度從而就高，迭代次數一般就會很高，會達到2,3000。

2） 平滑度的要求 從數值上要顯式計算高斯曲率，因而必須要求影象是二次可微的，即可以對影象求微分。

本文提到的高斯曲率濾波器，由於無需顯式計算高斯曲率，大大降低了計算複雜度，反而從微分幾何的角度，由影象的分段可展曲面去估計影象，這在處理此問題時，就會有如下優勢：

1） 在時間和收斂度上，比之前的演算法都要快！

2） 濾波器無需顯式計算高斯曲率！

3） 濾波器是無參的（備：迭代次數的引數不算在內的話，算無參），且易於實現，還可並行實現，matlab有40行程式碼，c++少於100行程式碼。

2.2 理論闡述

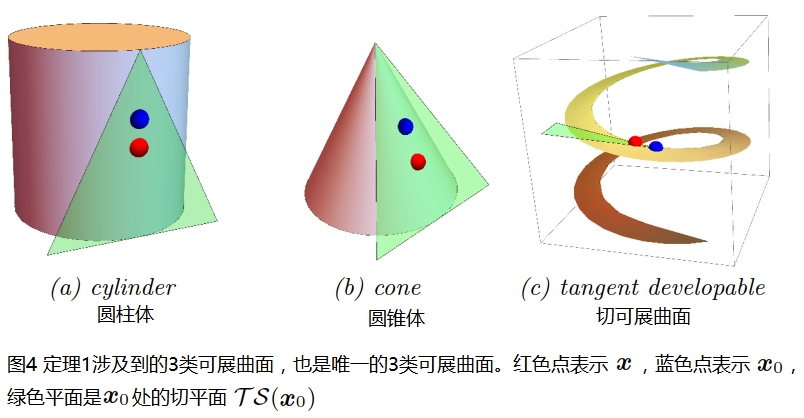
可展曲面可由其切平面區域性估計得到，如圖4所示：

另外，微分幾何中有定理1：

此定理的證明過程可以參考龔元浩老師的原文第134頁6.1.2.1節的證明。前面我們已知，二維影象中的高斯曲率定義為兩個主曲率的乘積，定理1告訴我們的是，任何可展曲面，雖然只有3個可展曲面，其任意點處的高斯曲率為零。因此，最小化其中任意一個主曲率，就相當於最小化高斯曲率！

定理1的結論即是高斯曲率濾波器的理論基礎！

由此，我們即可實現高斯曲率的最小化而無需進行高斯曲率的顯式計算，即如下式所示，最小化其中較小的主曲率即可實現高斯曲率的最小化：

2.3 域分解方法

區域性最小化主曲率絕對值的較小者，受限於相鄰畫素之間的關聯性，因此，提出了一種域分解方法，以去除相鄰畫素之間的依賴性。

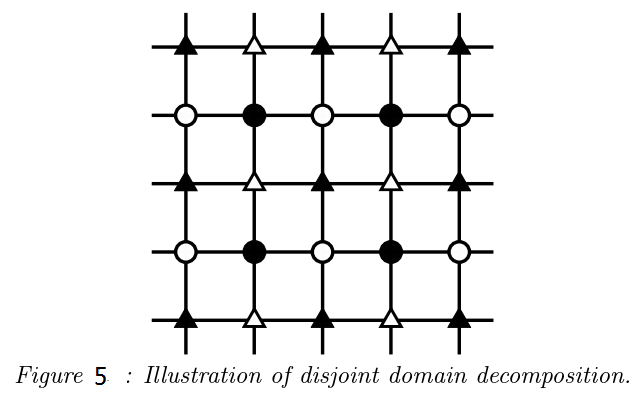
如圖5所示，將二維影象中的畫素點分成4類，即水平方向和垂直方向上的同類畫素點均不相鄰：

這種劃分實際上有3個好處：

1） 去除了相鄰畫素之間的依賴性；

2） 由於相鄰畫素之間的獨立性，當前畫素值的更新可以利用周圍已更新的畫素值，因為4類畫素的更新是獨立進行的，沒有先後次序，所以在更新某一類畫素時，可以利用周圍已經更新過的某些類畫素值；

3）在3×3區域性視窗中，所有切平面可以枚舉出來（切平面如何表示後續會介紹），因此近鄰投影（proximal projecting）能夠用於使得影象曲面更加可展，這就意味著可以區域性的降低高斯曲率；

通過定理1可知，我們需要將原始影象曲面U(x)投影到U`(x)，使得U`(x)在相鄰畫素的閉合切平面上。

首先，確定如何表示其切平面；

然後，確定如何選取投影方法；

2.4 切平面的表示方法

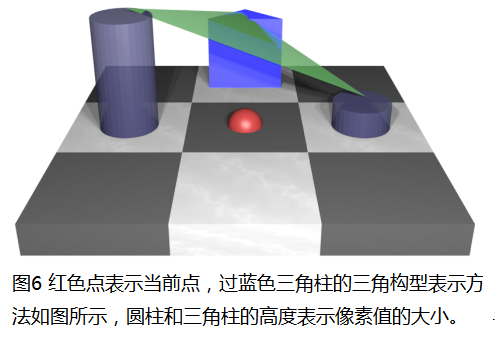
其實，有很多種切平面的表示方法（這在後續實際的應用上體現出了這種表示方法的多樣性），在本小節中，選取的是三角構型用於表示曲面的切平面，下面以黑色圓x與其3×3鄰域N(x)為例，如圖6所示：

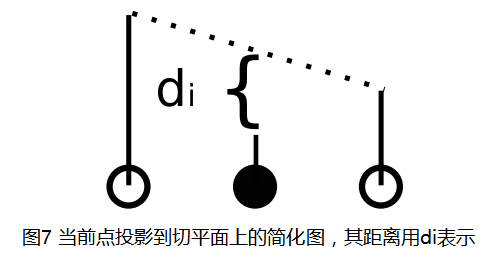
這是在此區域性視窗中的一個三角切平面，其他的列舉示例下一小節會介紹，得到此切平面之後，我們將紅色點，即當前點投影到綠色切平面上，就可以得到當前點到切平面的距離，如圖7所示：

2.5 列舉所有型別的投影

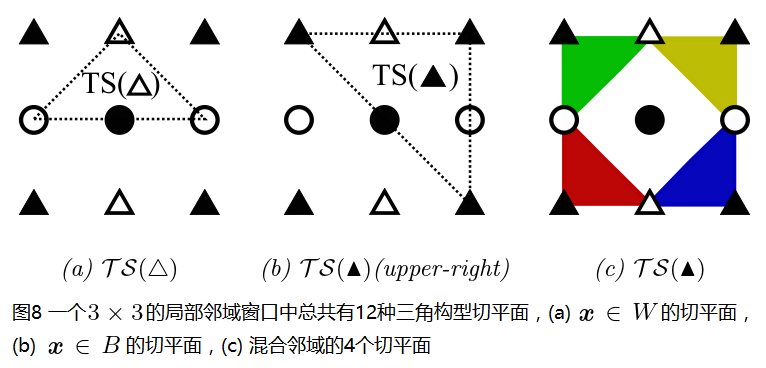
為了在區域性視窗N(x)中找到最小的投影距離di，需要將所有可能的三角構型切平面枚舉出來，如圖8所示：

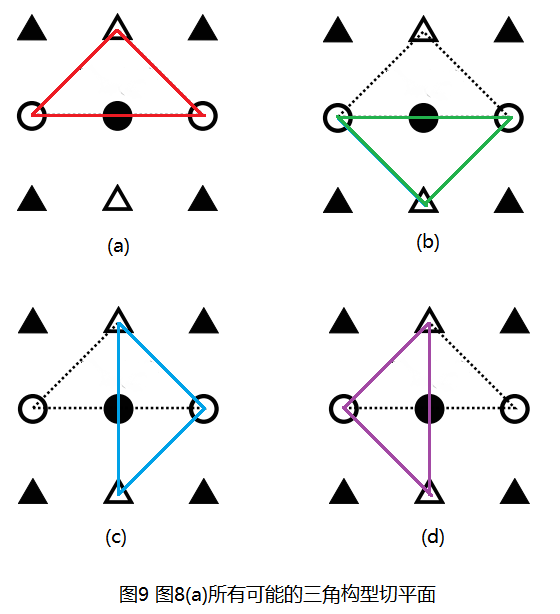
圖8(a)給出了一個示例，實際上，以黑色圓形點為中心點，切平面過白色點的三角構型切平面還有3種，也就是說圖8(a)中的切平面共有4種，如圖9所示：

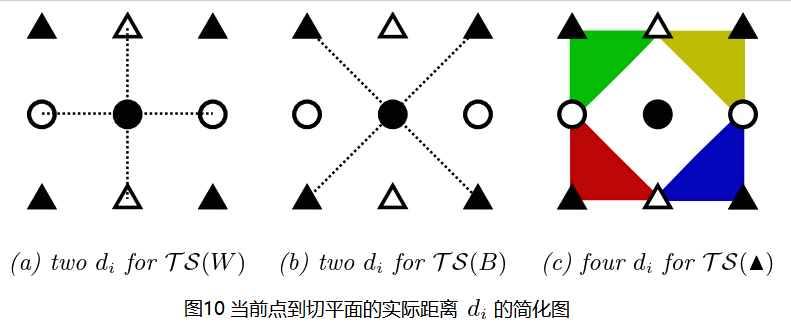
類似的圖8(b)也有4種，圖8(c)有4種，其全部給出，如此，在一個3×3的區域性視窗中，三角構型切平面共有12種情況，但是仔細看圖6和圖7可以看出，到切平面的距離di的實際情況沒有12種，按照圖7所示，圖8可以簡化為下圖：

以圖10(a)為例說明一下，黑色圓點到切平面的距離實際上就是黑色圓點到 ”白色圓-黑色圓-白色圓” 線段的距離，這種距離看圖7應該可以理解，圖10(b)(c)均好理解，這裡不贅述了。

2.6 最小投影運算元

圖2.5節可知，當前點到切平面的投影總共有8種，即當前點到切平面的距離共有8種，{di, i=1,2,...,8}，這裡使用8種投影距離的最小值作為投影運算元，更確切的說，令

然後，利用下式對原始影象的三維曲面進行計算：

完整的演算法數值實現虛擬碼如圖11所示：

圖11對應於原始論文的第140頁 Algorithm 11 。需要說明的是，基於Euler Theorem，我們有

其實，這個尤拉定理原始論文中也是直接給出的，沒有參考文獻可以參考，暫時這麼記住吧！ 上式中，k1 k2是兩個主曲率，theta(i) 是到主平面的角度，主平面可以參考圖3理解。因此，如果角度取樣theta(i) 在[-pi, +pi]內是足夠緻密的(dense enough)，可得 | dm | ≈ min{| ki |}，其中k1k2≥0，關於di的詳細介紹在下一章節中會重點介紹。

2.7 高斯曲率運算元

由於之前我們只是針對某一類，比如黑色三角形進行的詳細介紹，所以聯合其他三類的投影操作就構成了此高斯曲率濾波器，如圖12所示：

  

由於此四類畫素是相互獨立的，其迭代是互不影響的，因而可以並行運算。

2.8 收斂性證明

在證明高斯曲率濾波器之前，首先證明每一步最小投影運算元都可以降低高斯曲率能量E(U)，然後再證明高斯曲率濾波器能夠降低總能量。

證明：4類畫素只需要證明其中一種即可，其餘類似，

換句話說，高斯曲率能量是相對於n的單調函式，又能量肯定是對於零的，由單調有界定理可知，高斯曲率濾波器演算法2是收斂的。

2.9 小結

其實到這裡，曲率濾波的理論部分全都介紹完了，

好吧，又有事耽擱了，先放在這。。。鬱悶