原作者：WangBo_NLPR 原文：https://blog.csdn.net/walilk/article/details/50978864 
原作者：Eric_LH 原文：https://blog.csdn.net/eric_lh/article/details/78994461 

--------------------- 

前言
　機器學習中的大部分問題都是優化問題，而絕大部分優化問題都可以使用梯度下降法處理，那麼搞懂什麼是梯度，什麼是梯度下降法就非常重要！這是基礎中的基礎，也是必須掌握的概念！
　提到梯度，就必須從導數（derivative）、偏導數（partial derivative）和方向導數（directional derivative）講起，弄清楚這些概念，才能夠正確理解為什麼在優化問題中使用梯度下降法來優化目標函式，並熟練掌握梯度下降法（Gradient Descent）。

　本文主要記錄我在學習機器學習過程中對梯度概念複習的筆記，主要參考《高等數學》《簡明微積分》以及維基百科上的資料為主，文章小節安排如下：
　1）導數
　2）導數和偏導數
　3）導數與方向導數
　4）導數與梯度
　5）梯度下降法

導數
　一張圖讀懂導數與微分：
　

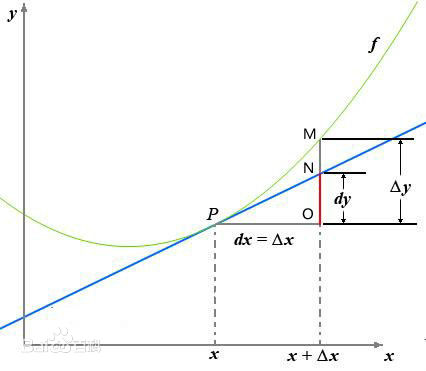
　這是高數中的一張經典圖，如果忘記了導數微分的概念，基本看著這張圖就能全部想起來。
　導數定義如下：
　

　反映的是函式y=f(x)在某一點處沿x軸正方向的變化率。再強調一遍，是函式f(x)在x軸上某一點處沿著x軸正方向的變化率/變化趨勢。直觀地看，也就是在x軸上某一點處，如果f’(x)>0，說明f(x)的函式值在x點沿x軸正方向是趨於增加的；如果f’(x)<0，說明f(x)的函式值在x點沿x軸正方向是趨於減少的。

　這裡補充上圖中的Δy、dy等符號的意義及關係如下：
　Δx：x的變化量；
　dx：x的變化量Δx趨於0時，則記作微元dx；
　Δy：Δy=f(x0+Δx)-f(x0)，是函式的增量；
　dy：dy=f’(x0)dx，是切線的增量；
　當Δx→0時，dy與Δy都是無窮小，dy是Δy的主部，即Δy=dy+o(Δx).
　

導數和偏導數
　偏導數的定義如下：
　

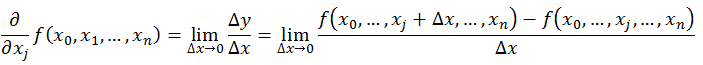
　可以看到，導數與偏導數本質是一致的，都是當自變數的變化量趨於0時，函式值的變化量與自變數變化量比值的極限。直觀地說，偏導數也就是函式在某一點上沿座標軸正方向的的變化率。
　區別在於：
　導數，指的是一元函式中，函式y=f(x)在某一點處沿x軸正方向的變化率；
　偏導數，指的是多元函式中，函式y=f(x1,x2,…,xn)在某一點處沿某一座標軸（x1,x2,…,xn）正方向的變化率。
　

導數與方向導數
　方向導數的定義如下：
　

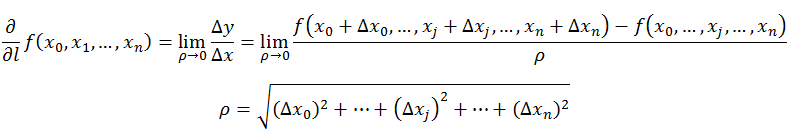
　在前面導 數和偏導數的定義中，均是沿座標軸正方向討論函式的變化率。那麼當我們討論函式沿任意方向的變化率時，也就引出了方向導數的定義，即：某一點在某一趨近方向上的導數值。
　通俗的解釋是：
　我們不僅要知道函式在座標軸正方向上的變化率（即偏導數），而且還要設法求得函式在其他特定方向上的變化率。而方向導數就是函式在其他特定方向上的變化率。
　

導數與梯度
　梯度的定義如下：
　 

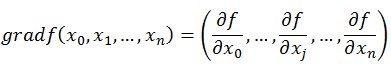
　梯度的提出只為回答一個問題：
　函式在變數空間的某一點處，沿著哪一個方向有最大的變化率？
　梯度定義如下：
　函式在某一點的梯度是這樣一個向量，它的方向與取得最大方向導數的方向一致，而它的模為方向導數的最大值。
　這裡注意三點：
　1）梯度是一個向量，即有方向有大小；
　2）梯度的方向是最大方向導數的方向；
　3）梯度的值是最大方向導數的值。
　

導數與向量
　提問：導數與偏導數與方向導數是向量麼？
　向量的定義是有方向（direction）有大小（magnitude）的量。
　從前面的定義可以這樣看出，偏導數和方向導數表達的是函式在某一點沿某一方向的變化率，也是具有方向和大小的。因此從這個角度來理解，我們也可以把偏導數和方向導數看作是一個向量，向量的方向就是變化率的方向，向量的模，就是變化率的大小。
　那麼沿著這樣一種思路，就可以如下理解梯度：
　梯度即函式在某一點最大的方向導數，函式沿梯度方向函式有最大的變化率。
　
　

梯度下降法
　既然在變數空間的某一點處，函式沿梯度方向具有最大的變化率，那麼在優化目標函式的時候，自然是沿著負梯度方向去減小函式值，以此達到我們的優化目標。
　如何沿著負梯度方向減小函式值呢？既然梯度是偏導數的集合，如下：
　

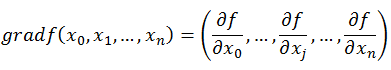
　同時梯度和偏導數都是向量，那麼參考向量運演算法則，我們在每個變數軸上減小對應變數值即可，梯度下降法可以描述如下：
　

　以上就是梯度下降法的由來，大部分的機器學習任務，都可以利用Gradient Descent來進行優化。
--------------------- 

總結：

1.導數定義： 導數代表了在自變數變化趨於無窮小的時候，函式值的變化與自變數的變化的比值。幾何意義是這個點的切線。物理意義是該時刻的（瞬時）變化率。

注意：在一元函式中，只有一個自變數變動，也就是說只存在一個方向的變化率，這也就是為什麼一元函式沒有偏導數的原因。
（derivative）

2.偏導數： 既然談到偏導數，那就至少涉及到兩個自變數。以兩個自變數為例，z=f（x,y），從導數到偏導數，也就是從曲線來到了曲面。曲線上的一點，其切線只有一條。但是曲面上的一點，切線有無數條。而偏導數就是指多元函式沿著座標軸的變化率。
注意：直觀地說，偏導數也就是函式在某一點上沿座標軸正方向的的變化率。
（partial derivative）

3.方向導數: 在某點沿著某個向量方向上的方向導數，描繪了該點附近沿著該向量方向變動時的瞬時變化率。這個向量方向可以是任一方向。

方向導數的物理意義表示函式在某點沿著某一特定方向上的變化率。
注意：導數、偏導數和方向導數表達的是函式在某一點沿某一方向的變化率，也是具有方向和大小的。
（directional derivative）

4.梯度: 函式在給定點處沿不同的方向，其方向導數一般是不相同的。那麼沿著哪一個方向其方向導數最大，其最大值為多少，這是我們所關心的，為此引進一個很重要的概念: 梯度。

5.梯度下降
在機器學習中往往是最小化一個目標函式 L(Θ)，理解了上面的內容，便很容易理解在梯度下降法中常見的引數更新公式：

Θ = Θ − γ ∂ L ∂ Θ
通過算出目標函式的梯度（算出對於所有引數的偏導數）並在其反方向更新完引數 Θ ，在此過程完成後也便是達到了函式值減少最快的效果，那麼在經過迭代以後目標函式即可很快地到達一個極小值。

6.In summary:
概念 　　物理意義
導數 　　函式在該點的瞬時變化率
偏導數 　函式在座標軸方向上的變化率
方向導數 函式在某點沿某個特定方向的變化率
梯度 　　函式在該點沿所有方向變化率最大的那個方向