《Inception V3-Rethinking the Inception Architecture for Computer Vision》論文筆記

阿新 • • 發佈：2018-11-02

1. 論文思想

在其它條件都滿足的（資料充足且足夠好）的情況下，增加模型的尺寸以及計算量會帶來實質上的優勢，但是可供計算的資源總是有限的，特別是在移動裝置上，並不能無節制的增加模型的尺寸。例如，在VggNet模型中使用的引數量是AlexNet引數量的三倍，實際取得的效果也是好於AlexNet的。在之前的Google-Net中採用了優化之後的Inception-V1結構以及去掉全連線層等方式使得模型的引數量為500W資料量，相比VggNet的6000W數量及的引數量，後者是前者的12倍。

2. 通用設計準則

這裡給出基於大規模各式各樣卷積網路實踐的準則。這些準則是推測性質的，需要後期的實驗去評估他們的精度以及可用的領域。在實際中偏移這些準則過多會導致網路惡化，而修正這些偏差通常會使得網路更優。

（1）避免網路表達瓶頸，特別是網路結構的前期。對於深度學習網路可以使用一個無環圖進行表示，這就對網路中資訊的流向做了明確的規定。通常來說從網路的輸入端到最後的輸出端網路的表達尺寸是緩慢減小的。
（2）更高維度的表示在網路中更容易區域性處理。在卷積網路中增加每個圖塊的啟用允許更多解耦的特徵。所產生的網路將訓練更快
（3）空間聚合可以通過更低維度的植入來實現，這個過程中不會損失過多或是不會損失表達的能力。例如，在使用大尺寸卷積的時候，將其輸入維度減小，並不會對預期帶來不利的影響。我們假設，如果在空間聚合上下文中使用輸出，則相鄰單元之間的強相關性會導致維度縮減期間的資訊損失少得多。鑑於這些訊號應該易於壓縮，因此尺寸減小甚至會促進更快的學習。
（4）平衡網路的寬度與深度。網路的最佳效能體現是由每個階段的濾波器組數量以及網路的深度取平衡得到的。同時增加網路的深度以及濾波器數量會使得網路效能提升。但是，在一定的計算量前提下亮著共同增加會使得網路達到最優提升。因而就需要在一定的計算量前提下在網路深度以及濾波器的數量上去的一個均衡值。

3. 大濾波器尺寸卷積的因式分解

GoogleNet的大量初始好處都是來自於降維，可以視為在卷積層上的因式分解，這時在計算效率層面的一中特殊案例。其在 $1*1$ 的卷積核之後接 $3 * 3$

3 $3*3$ 的卷積。在視覺任務中，我們希望啟用層的鄰近輸出是高度相關的。因而，我們可以預期，他們在聚合之前被減少，這將導致區域性表達具有相似性

3.1 因式分解到更小的卷積

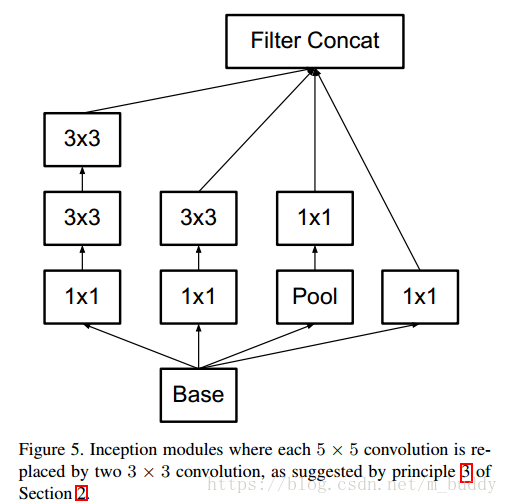
大的卷積核（例如， $7*7$ 或是 $5*5$ ）會帶來不協調的計算開銷。例如， $5*5$ 的卷積核是 $3*3$ 大小卷積核引數的 $25/9=2.78$ 倍。因而，使用 $5*5$ 大小的卷積帶來的計算量消耗是大於 $3*3$ 的。且 $5*5$ 大小的卷積核在模型前期的時候可以用來感受更大的視野，也是有其存在的價值與意義。針對這樣的情況可以對其使用兩個 $3*3$ 大小的卷積核來代替，減少引數量。其執行示意圖如下：
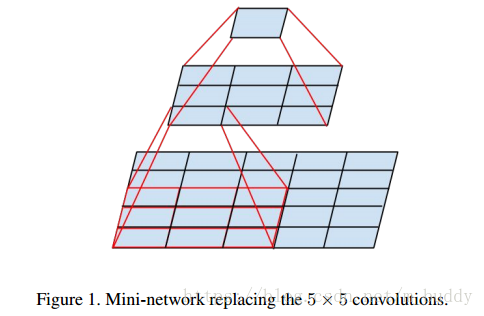
這裡寫圖片描述
下圖是原論文中採用的Inception結構：

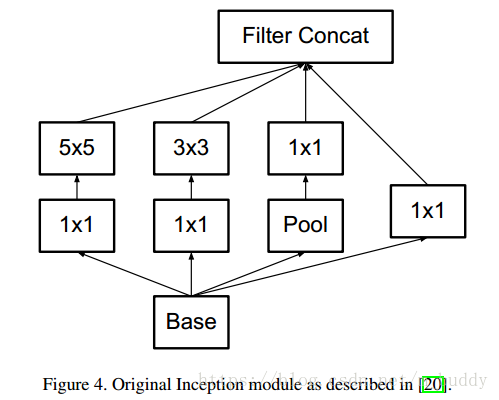
使用因式分解之後得到的結構：

3.2 空間因式分解到部隊稱的卷積

在上面的內容中將大於 $3*3$ 大小的可以因式分解為一系列 $3*3$ 大小的卷積核。那麼 $3*3$ 大小的卷積核是否可以分解成為更小的卷積核連線呢？答案是肯定的，文章中使用 $n*1$ 大小的卷積核作為替換，就如下圖所示：
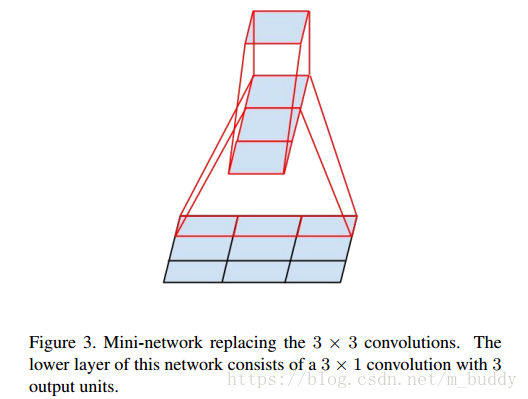
這裡寫圖片描述
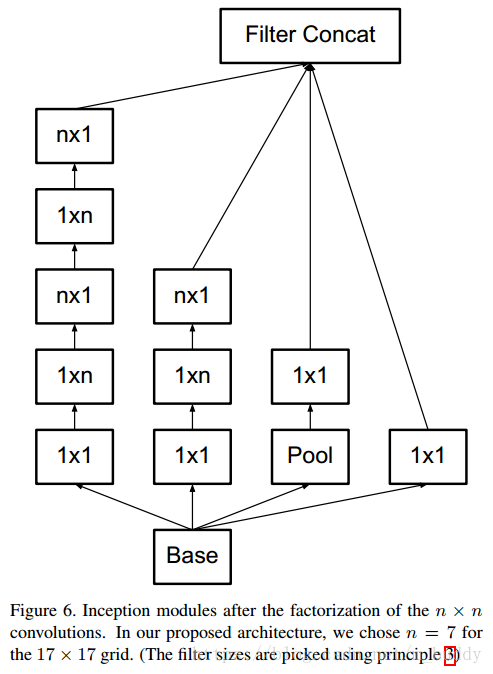
在上圖中原本 $3*3$ 大小的卷積可以通過級聯 $1*3$ 與 $3*1$ 的卷積實現相同的感受視野。而且比原來的引數量節省了 $\frac{2}{3}$ 的引數量。當然這種思路可以推廣到任意的 $n*n$ 的卷積核上去。如下圖所示：

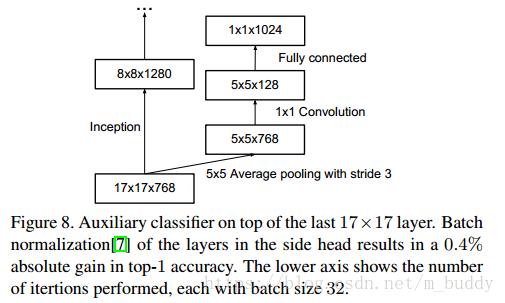
4. 附加損失函式使用

在之前的GoogleNet論文中提到新增附加損失函式會給網路帶來附加的梯度資訊，從而避免了梯度消失的問題。在論文中發現輔助損失函式並不能幫助網路儘早收斂，但是會使得網路獲得更高一些的精確率。並認為附加損失函式的加入最網路加入了正則約束。
這裡寫圖片描述

5. 有效的網格尺寸減少

傳統上，卷積網路使用一些池化操作來縮減特徵圖的網格大小。為了避免表示瓶頸，在應用最大池化或平均池化之前，需要擴充套件網路濾波器的啟用維度。例如，開始有一個帶有 $k$ 個濾波器的 $d*d$ 網格，如果我們想要達到一個帶有 $2k$ 個濾波器的 $\frac{d}{2}*\frac{d}{2}$ 網格，我們首先需要用 $2k$ 個濾波器計算步長為1的卷積，然後應用一個額外的池化步驟。這意味著總體計算成本由在較大的網格上使用 $2d^2k^2$ 次運算的昂貴卷積支配。一種可能性是轉換為帶有卷積的池化，因此導致 $2(\frac{d}{2})^2k^2$ 次運算，將計算成本降低為原來的四分之一。然而，由於表示的整體維度下降到 $(\frac{d}{2})^2k$ ，會導致表示能力較弱的網路，這會產生一個表示瓶頸。見下圖
這裡寫圖片描述
上圖中，減少網格尺寸的兩種替代方式。左邊的解決方案違反了第2節中不引入表示瓶頸的原則1。右邊的版本計算量昂貴3倍
我們建議另一種變體，其甚至進一步降低了計算成本，同時消除了表示瓶頸（見下圖），而不是這樣做。我們可以使用兩個平行的步長為2的塊：PP和CC。PP是一個池化層（平均池化或最大池化）的啟用，兩者都是步長為2，其濾波器組連線下圖所示。
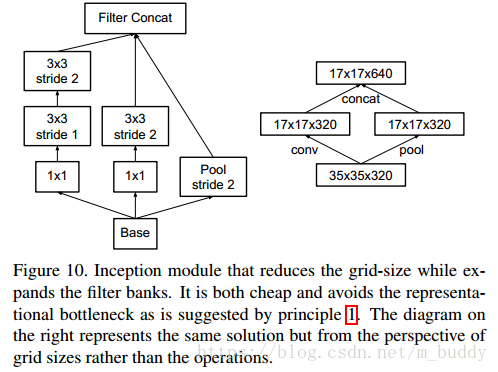
這裡寫圖片描述
縮減網格尺寸的同時擴充套件濾波器組的Inception模組。它不僅廉價並且避免了原則1中提出的表示瓶頸。右側的圖表示相同的解決方案，但是從網格大小而不是運算的角度來看。

《Inception V3-Rethinking the Inception Architecture for Computer Vision》論文筆記

1. 論文思想在其它條件都滿足的（資料充足且足夠好）的情況下，增加模型的尺寸以及計算量會帶來實質上的優勢，但是可供計算的資源總是有限的，特別是在移動裝置上，並不能無節制的增加模型的尺寸。例如，在VggNet模型中使用的引數量是AlexNet引數量的三倍，實際取得的效果也是好於Ale

《Rethinking the Inception Architecture for Computer Vision》筆記

介紹深度學習在計算機視覺方面取得了很大突破。在2014ILSVRC分類比賽中中，VGG和GoogLeNet取得了優異成績。卷積網路架構上的改進可以提升計算機視覺各類任務的效能。 VGG以很樸素的方式描述了特徵，但有很大的計算量。GoogLeNet

【Network architecture】Rethinking the Inception Architecture for Computer Vision（inception-v3）論文解析

傳統 tps 聚合更遠瓶頸 orm -o 分類每一個 0. paper link inception-v3 1. Overview ??這篇文章很多“經驗”性的東西，因此會寫的比較細，把文章裏的一些話摘取出來，多學習一下，希望對以後自己設計網絡有幫助。 2. Four

網路模型 Inception V2/V3-Rethinking the Inception Architecture for Computer Vision

本文是對 GoogleNet 網路模型 Inception 架構的重思考和改進，Inception V3, 其中 Going deeper with convolutions 是 Inception V1, Batch Normalization 是 I

Python計算機視覺深度學習三合一Deep learning for computer vision with Python高清pdf

Deep Learning for Computer Vision with Python Starter Bundle pdf Deep Learning for Computer Vision with Python Practitioner Bundle pdf Deep Learning for

Towards understanding Probability and Statistics for computer vision

Introduction to independenceFirst, let’s talk about “independence”. Do you remember the joint probability that we talked last time? In short, joint probabi

Generating Large, Synthetic, Annotated, & Photorealistic Datasets for Computer Vision

I’d like to introduce you to the beta of a tool we’ve been working on at Greppy, called the Greppy Metaverse, which assists with computer vision object rec

What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?

原論文連結一、摘要：主要有兩大類不確定性，偶然不確定性（aleatoric uncertainty）和認知不確定性（epistemic uncertainty），偶然不確定性用來描述觀測中固有的噪聲；認知不確定性則是用來描述模型中的不確定性。認知不確定性

Selective Search for Object Recognition 論文筆記【圖片目標分割】

line 單個介紹 images 分層什麽但是如果抽樣這篇筆記，僅僅是對選擇性算法介紹一下原理性知識，不對公式進行推倒. 前言：這篇論文介紹的是，如果快速的找到的可能是物體目標的區域，不像使用傳統的滑動窗口來暴力進行區域識別.這裏是使用算法從多個維度對找

A Benchmark Comparsion of Monocular Visual-Inertial Odometry Algorithms for Flying Robots論文筆記

模型 fas con patch 最小耦合而且測試平臺 style 摘要：　　本文主要比較單目VIO的算法在飛行機器人上運行的性能，測試使用統一數據集為EuRoC。其中評價指標為：姿態估計精度、每幀處理時間以及CPU和內存負載使用率，同時還有RMSE（運行軌跡與真實

Feature Pyramid Networks for Object Detection 論文筆記

版權宣告：本文為博主原創文章，未經博主允許不得轉載。 https://blog.csdn.net/Jesse_Mx/article/details/54588085 論文地址：Feature Pyramid Networks for Object Detection 前言這篇論文主要使

Feature Pyramid Networks for Object Detection論文筆記

1、摘要 Feature pyramids are a basic component in recognition systems for detecting objects at diferent scales.But recent deep learning object detector

蒸餾神經網路(Distill the Knowledge in a Neural Network) 論文筆記蒸餾神經網路(Distill the Knowledge in a Neural Network) 論文筆記

轉蒸餾神經網路(Distill the Knowledge in a Neural Network) 論文筆記 2017年08月06日 16:19:48 haoji00

《Computer vision》筆記-GoodLeNet（3）

Quantization Mimic: Towards Very Tiny CNN for Object Detection 論文筆記

兩種 detect 不同展示沒有 bsp 中學 ant ans 摘要　　在本文中，我們提出了一個簡單而通用的框架，用於訓練非常微小的CNN（例如，通道數減少到1/32的VGG）用於目標檢測。由於表示能力有限，為檢測等復雜任務訓練非常小的網絡具有挑戰性。據我們

【Network Architecture】Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning（轉） Feature Extractor[Inception v4]

文章來源： https://www.cnblogs.com/shouhuxianjian/p/7786760.html Feature Extractor[Inception v4] 0. 背景隨著何凱明等人提出的ResNet v1，google這邊坐

《Inception V3-Rethinking the Inception Architecture for Computer Vision》論文筆記

1. 論文思想

2. 通用設計準則

3. 大濾波器尺寸卷積的因式分解

3.1 因式分解到更小的卷積

3.2 空間因式分解到部隊稱的卷積

4. 附加損失函式使用

5. 有效的網格尺寸減少

《Inception V3-Rethinking the Inception Architecture for Computer Vision》論文筆記

《Rethinking the Inception Architecture for Computer Vision》筆記

【Network architecture】Rethinking the Inception Architecture for Computer Vision（inception-v3）論文解析

網路模型 Inception V2/V3-Rethinking the Inception Architecture for Computer Vision

Python計算機視覺深度學習三合一Deep learning for computer vision with Python高清pdf

Towards understanding Probability and Statistics for computer vision

Generating Large, Synthetic, Annotated, & Photorealistic Datasets for Computer Vision

What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?

Selective Search for Object Recognition 論文筆記【圖片目標分割】

A Benchmark Comparsion of Monocular Visual-Inertial Odometry Algorithms for Flying Robots論文筆記

Feature Pyramid Networks for Object Detection 論文筆記

Feature Pyramid Networks for Object Detection論文筆記

蒸餾神經網路(Distill the Knowledge in a Neural Network) 論文筆記蒸餾神經網路(Distill the Knowledge in a Neural Network) 論文筆記

《Computer vision》筆記-GoodLeNet（3）

Quantization Mimic: Towards Very Tiny CNN for Object Detection 論文筆記

【Network Architecture】Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning（轉） Feature Extractor[Inception v4]

1、VGG16 2、VGG19 3、ResNet50 4、Inception V3 5、Xception介紹——遷移學習

8-3下載inception-v3時遇到的問題

運用java 呼叫tensorflow中的inception v3模型

實驗二：對Inception v3模型的對抗樣本

《Inception V3-Rethinking the Inception Architecture for Computer Vision》論文筆記

1. 論文思想

2. 通用設計準則

3. 大濾波器尺寸卷積的因式分解

3.1 因式分解到更小的卷積

3.2 空間因式分解到部隊稱的卷積

4. 附加損失函式使用

5. 有效的網格尺寸減少

相關推薦