題意：給定一個2*n的矩形方格，每個格子有一個權值，從（0,0）開始出發，要求遍歷完整個網格（不能重複走一個格子），求最大權值和，（權值和是按照step*w累加，step步數從0開始）。

題解：一開始我的想法是用dfs來求取最大的目標值，提交後tle,自己加了幾個剪枝也是tle,由於n最大是3e5，可以說是很大了，單純深搜很費時間，後來看了別人的部落格，發現可以用字首和來做（其他人也有的是用dp）

轉載：

題解:思維題,如果正向考慮的話很容易把自己繞暈,我們需要反過來想,你會發現其實對於一個2*N的矩陣,你一共只有N個終點(如下圖1),如果在認真推敲,你會發現對於這n個終點,從起點到終點的路線都是很有規律的,只有下圖2和3兩種情況)那麼問題就簡單了,只需要考慮各種字首的預處理,之後直接O(n)判斷這N個終點得到的最大貢獻即可~

圖一

圖二

圖三

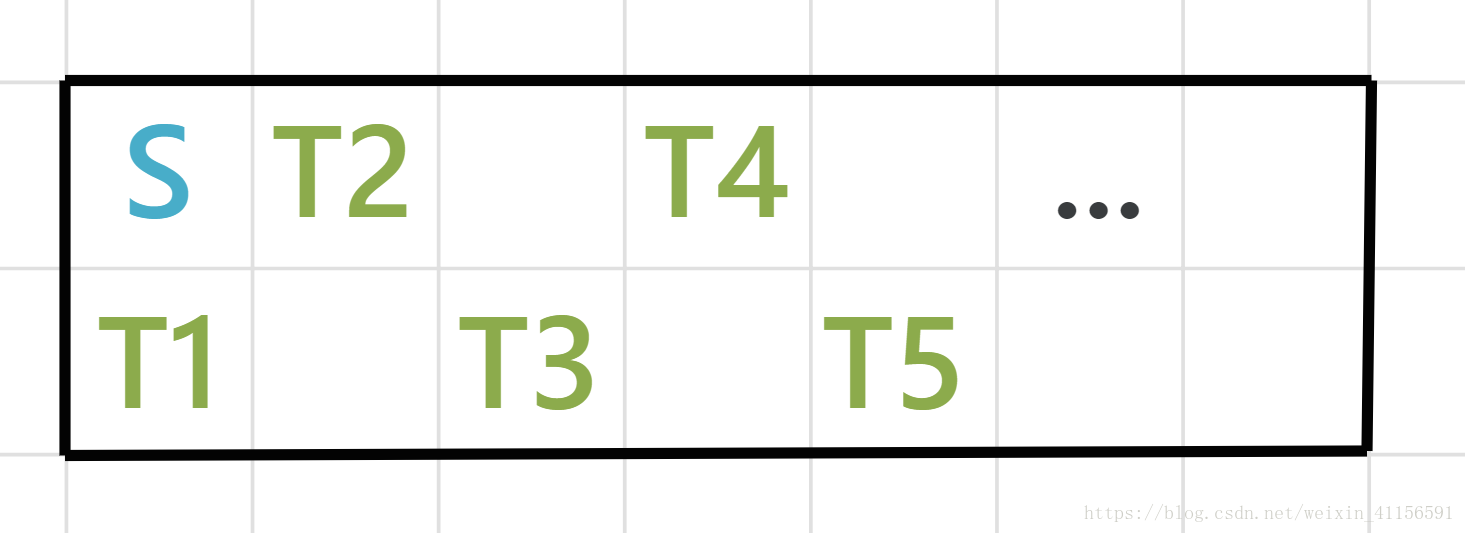
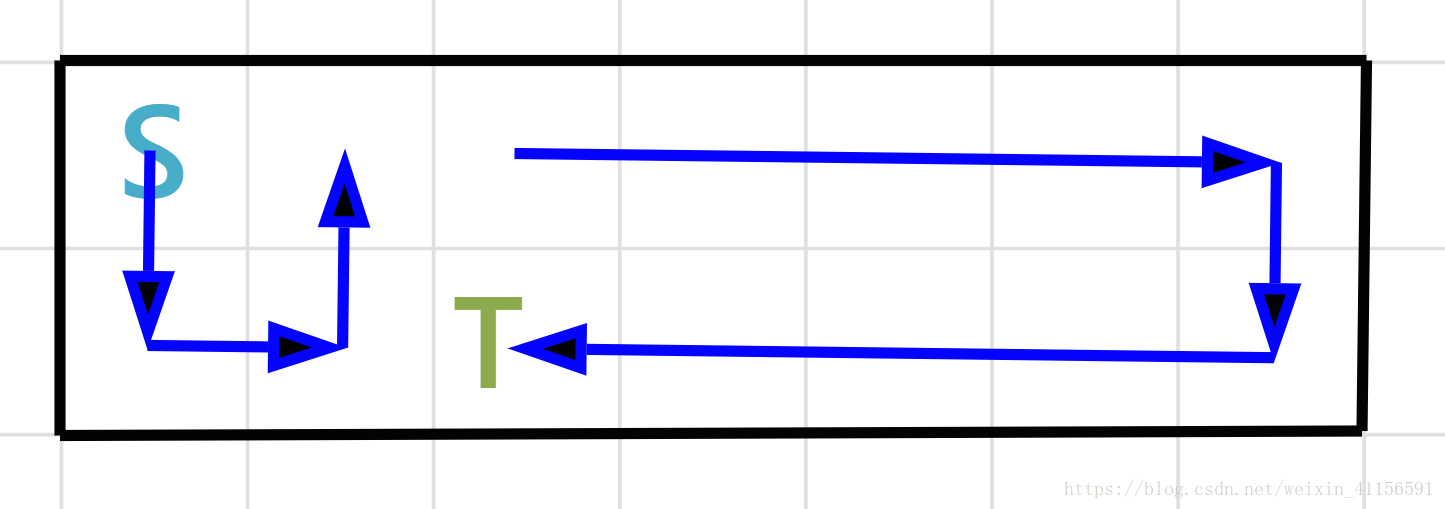
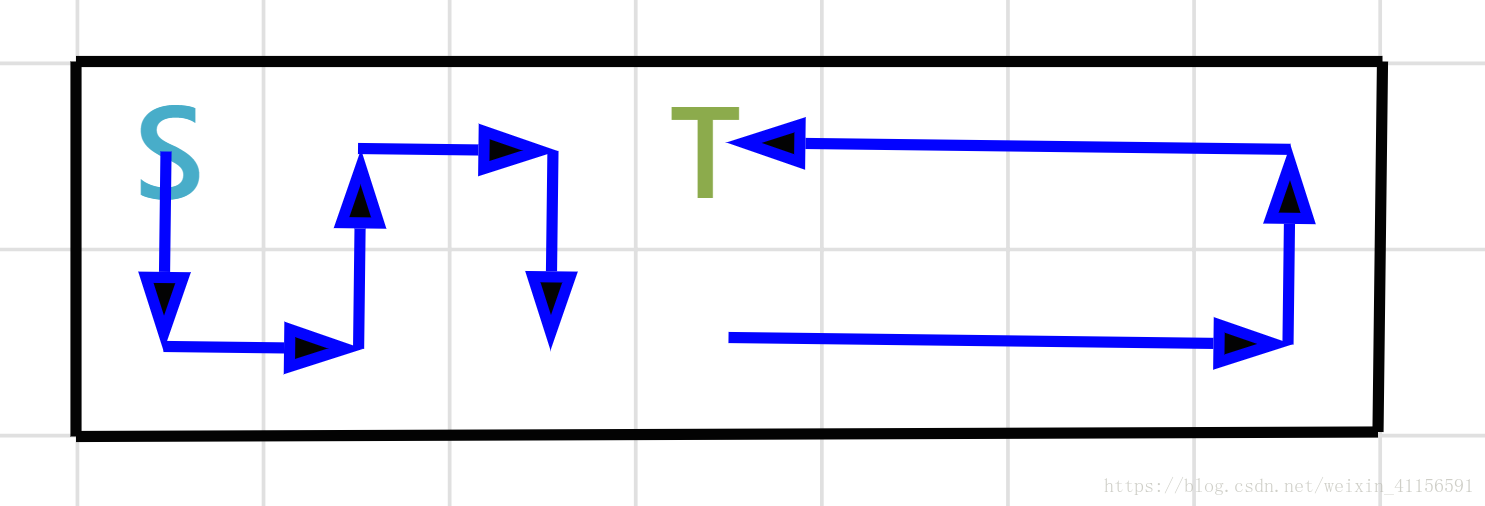
可以發現需要得到的是每個終點左邊的貢獻和右邊的貢獻,左邊的貢獻都是蛇形的,只用處理一個數組儲存,右邊由於有順時針和逆時針,所有需要處理2個數組維護字首和等~

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include <vector>
#include<queue>
#include <stack>
#include <map>
#define maxn 605005
#define INF 0x3f3f3f3f
#define LL long long
using namespace std;
LL n;
LL a[maxn];
LL b[maxn];
LL sum_s[maxn];//順時針的從1~2n的字首和
LL sum_n[maxn];//逆時針的從1~2n的字首和
LL sumpre[maxn];//取i~n列的a[i]+b[i]和
LL suml[maxn];//對於一種路線中的左邊部分
LL sumr[maxn];//同理，右邊部分
LL ans;
void solve()
{
   for(int i=n;i>=1;i--)
   {
      sumpre[i]=sumpre[i+1]+a[i]+b[i];
   }

   for(int i=1;i<=n;i++)
   {
      sum_s[i]=sum_s[i-1]+(i-1)*a[i];
      sum_n[i]=sum_n[i-1]+(i-1)*b[i];
   }
   for(int i=n;i>=1;i--)
   {
      sum_s[2*n-i+1]=sum_s[2*n-i]+(2*n-i)*b[i];
      sum_n[2*n-i+1]=sum_n[2*n-i]+(2*n-i)*a[i];
   }
   for(int i=1;i<=n;i++)//這裡分奇數和偶數考慮
   {
      if(i%2==1)
      {
         suml[i]=suml[i-1]+(2*i-3)*a[i-1]+(2*i-4)*b[i-1];
         sumr[i]=sum_s[2*n-i+1]-sum_s[i-1]+(i-1)*sumpre[i];
         //注意這裡要加(i-1)*sumpre[i]，仔細推磨
      }
      else
      {
         suml[i]=suml[i-1]+(2*i-4)*a[i-1]+(2*i-3)*b[i-1];
         sumr[i]=sum_n[2*n-i+1]-sum_n[i-1]+(i-1)*sumpre[i];
      }
   }
}
int main()
{
   ios::sync_with_stdio(false);
   cin>>n;
   for(int i=1;i<=n;i++)
   {
      cin>>a[i];
   }
   for(int i=1;i<=n;i++)
   {
      cin>>b[i];
   }
   solve();
   ans=0;
   for(int i=1;i<=n;i++)
   {
      ans=max(ans,suml[i]+sumr[i]);
      //suml[i]是i列之前,sumr[i]是i列（包括i列）之後的部分
      //比較所有方案
   }
   cout << ans << endl;
   return 0;
}