20172320 2018-2019-1 《Java程式設計》第七週學習總結
20172320 2018-2019-1 《Java程式設計》第七週學習總結
教材學習內容總結
- 二叉查詢樹是一種帶有附加屬性的二叉樹,即對樹中的每個結點,其左孩子都要小於其父節點,而父節點又要小於等於右孩子
- 二叉查詢樹的定義是二叉樹的擴充套件,因此操作是二叉樹中已定義的哪些操作的補充
| 操作 | 說明 |
|---|---|
| addElement | 往樹中新增一個元素 |
| removeElement | 從樹中刪除一個元素 |
| removeAllOccurrences | 從樹中刪除所指定元素的任何存在 |
| removeMin | 刪除樹中的最小元素 |
| removeMax | 刪除樹中的最大元素 |
| findMin | 返回一個指向樹中最小元素的引用 |
| findMax | 返回一個指向樹中最大元素的引用 |
- 有序列表的連結串列實現分析和二叉查詢樹實現分析
| 操作 | LinkedList | BinarySearchTreeList |
|---|---|---|
| removeFirst | O(1) | O(logn) |
| removeLast | O(n) | O(logn) |
| remove | O(n) | O(logn)* |
| first | O(1) | O(logn) |
| last | O(n) | O(logn) |
| contains | O(n) | O(logn) |
| isEmpty | O(1) | O(1) |
| size | O(1) | O(1) |
| add | O(n) | O(logn)* |
add操作和remove操作都可能導致樹變得不平衡
- 如果二叉查詢樹不平衡,其效率可能比線性結構還低,如蛻化樹
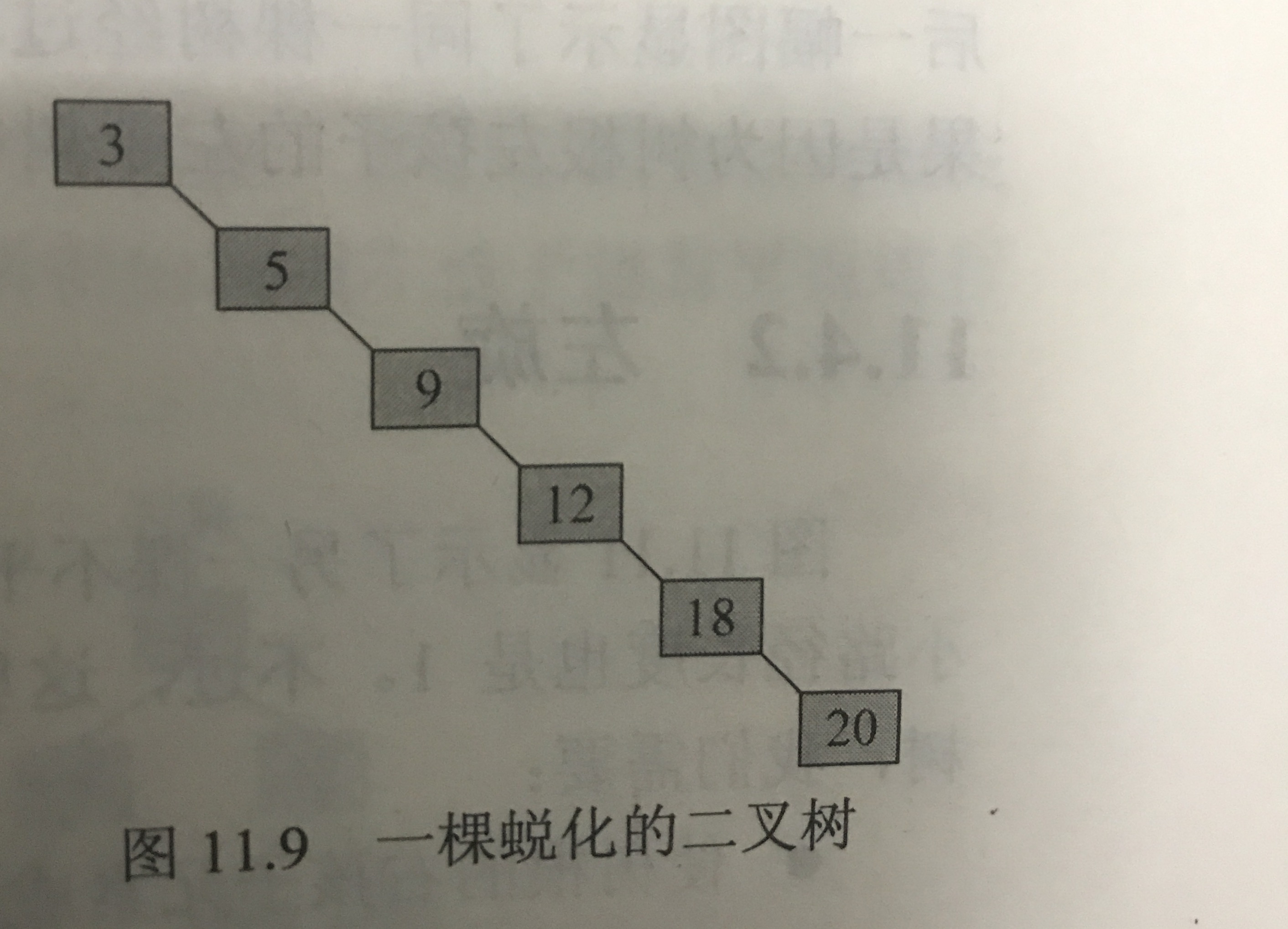
平衡化技術中通用的術語
◦右旋:左孩子繞著其父結點向右旋轉
◦使樹根的左孩子元素稱為新的根元素
◦使原跟元素成為這個新樹根的右孩子元素
◦使原樹根的左孩子的右孩子成為原樹根的新的左孩子

◦左旋:指右孩子繞其父節點向左旋轉
◦使樹根的右孩子元素成為新的根元素
◦使原樹根元素成為這個新樹根的左孩子元素
◦使原樹根右孩子結點的左孩子成為原樹根的新的右孩子

◦右左旋:對於由樹根右孩子的左子樹中較長路徑而導致的不平衡,必須先讓樹根右孩子的左孩子,繞著樹根的右孩子進行一次旋轉,然後再讓所得的樹根右孩子繞著樹根進行一次左旋
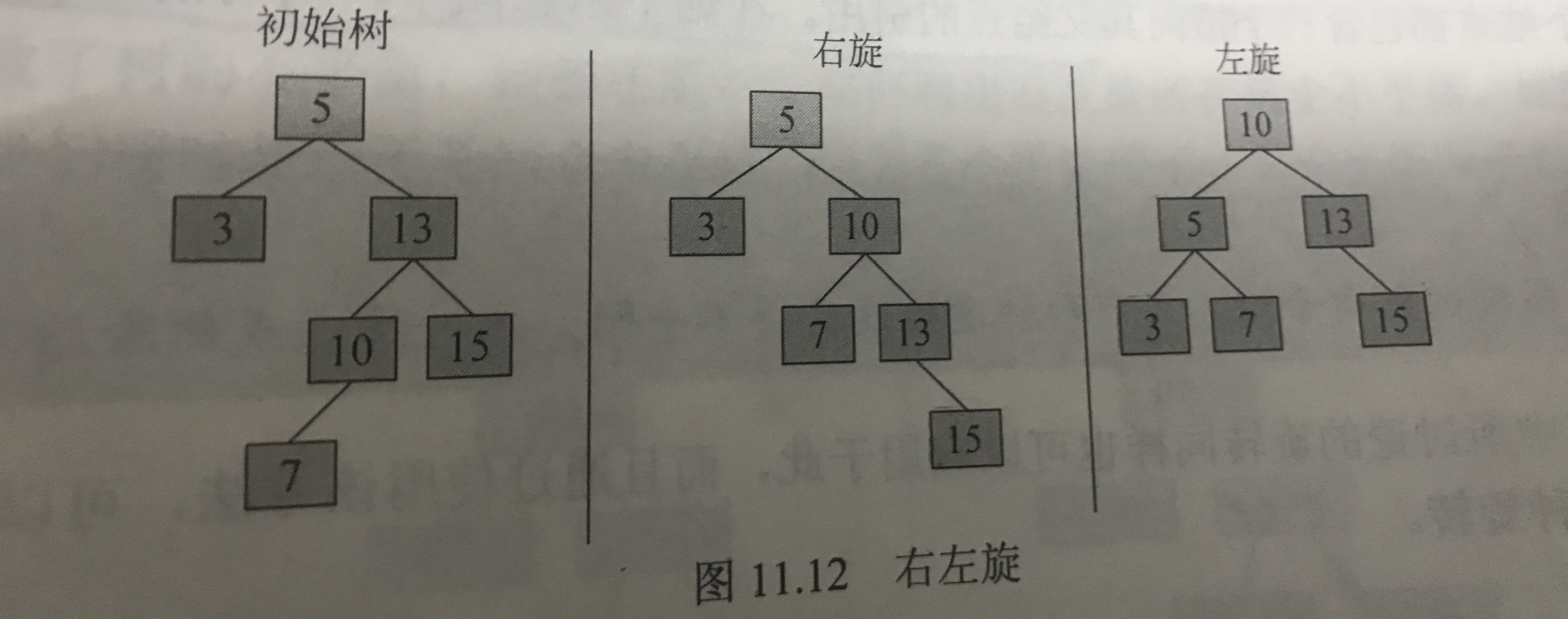
◦左右旋:對於由樹根左孩子的右子樹中較長路徑而導致的不平衡,必須先讓樹根左孩子的右孩子,繞著樹根的左孩子進行一次旋轉,然後再讓所得的樹根左孩子繞著樹根進行一次左旋

AVL樹
◦平衡化樹的一般性方法,自樹根而下的路徑最大長度必須不超過log2 n,而且自樹根而下的路徑最小長度必須不小於log2 n -1,AVL樹是上述樹的一種變體,ALV樹中任何兩個結點的高度差值最大不超過1
◦右子樹的高度減去左子樹的高度稱為該結點的平衡因子,若平衡因子大於1或小於-1,則以該結點為樹根的子樹需要重新平衡
◦樹或樹的任何子樹只有兩種途徑能變得不平衡:插入結點和刪除結點
◦AVL樹的右旋:如果某結點的平衡因子為-2,則意味著該結點的左子樹中有一條過長的路徑,若其左孩子的平衡因子為-1,則意味著較長的路徑處在這個左孩子的左子樹中,需將左孩子繞著初始結點進行一次右旋

◦AVL樹的左旋:如果某結點的平衡因子為+2,則意味著該結點的右子樹中有一條過長的路徑,若其右孩子的平衡因子為+1,則意味著較長的路徑處在這個右孩子的右子樹中,需將右孩子繞著初始結點進行一次左旋
◦AVL樹的右左旋:如果某結點的平衡因子為+2,則意味著該結點的右子樹中有一條過長的路徑,若其右孩子的平衡因子為-1,則意味著較長的路徑處在這個右孩子的左子樹中,則先讓初始結點右孩子的左孩子繞著初始結點的右孩子進行一次右旋,然後讓初始結點的右孩子繞著初始結點進行一次左旋
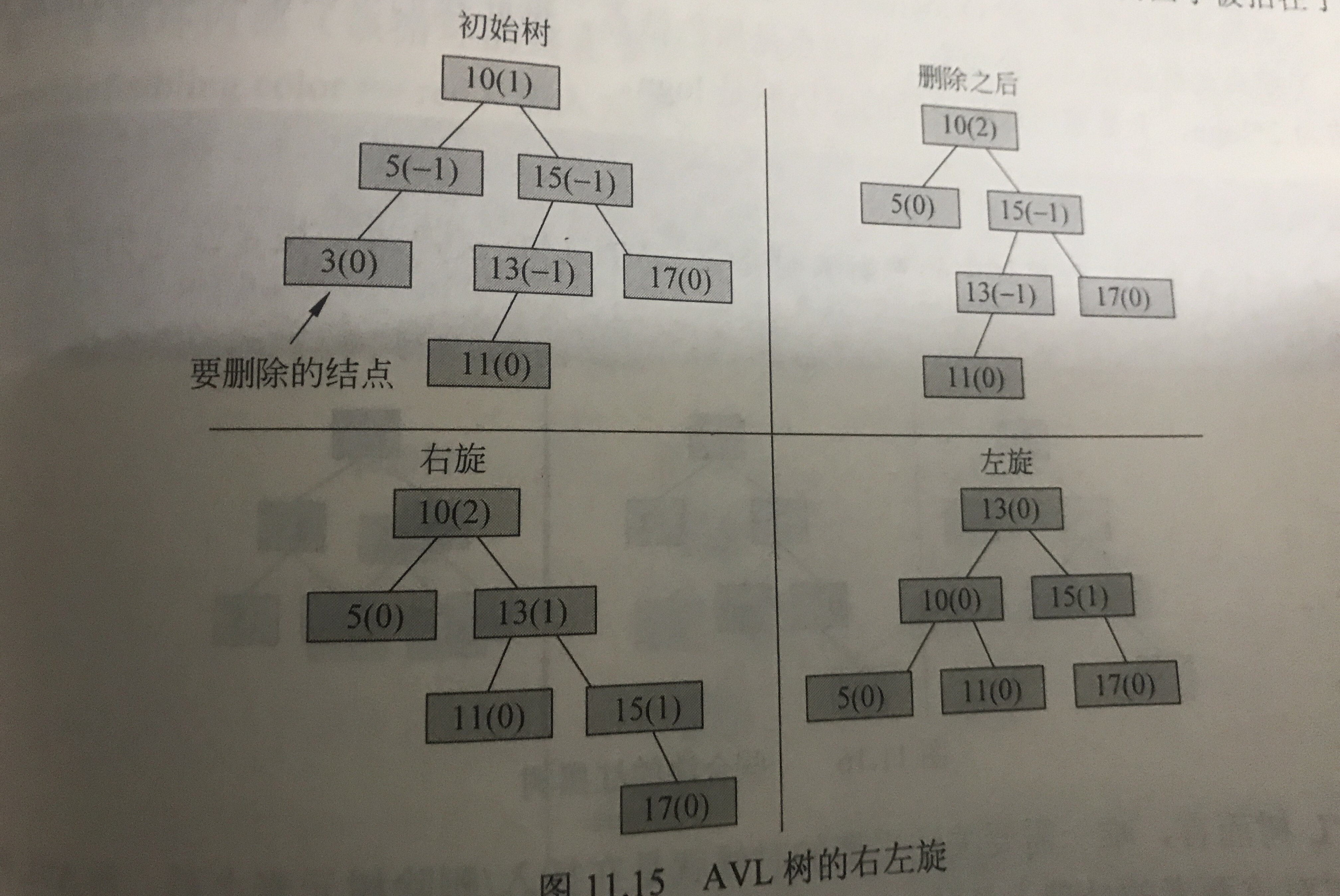
◦AVL樹的左右旋:如果某結點的平衡因子為-2,則意味著該結點的左子樹中有一條過長的路徑,若其左孩子的平衡因子為+1,則意味著較長的路徑處在這個左孩子的右子樹中,則先讓初始結點左孩子的右孩子繞著初始結點的左孩子進行一次左旋,然後讓初始結點的左孩子繞著初始結點進行一次右旋紅黑樹
◦規則
◦根結點為黑色
◦紅色結點的所有孩子都為黑色
◦從樹根到樹葉的每條路徑都包含同樣數目的黑色結點
◦紅黑樹中的平衡限制沒有AVL樹嚴格,但它們的序仍然是logn
◦紅黑樹元素插入
◦把新元素的顏色設為紅色
◦插入元素後,重新平衡化該樹,根據需要改變元素的顏色
◦設定樹根的顏色為黑色

教材中遇到的問題和解決過程
- 問題1:AVL樹與紅黑樹的區別
- 解決方案: ◦AVL 樹因其平衡的限制,可以始終保持 O(logn) 的時間複雜度
◦AVL是嚴格的平衡樹,因此在增加或者刪除節點的時候,根據不同情況,旋轉的次數比紅黑樹要多
◦紅黑樹是用非嚴格的平衡來換取增刪節點時候旋轉次數的降低開銷
◦搜尋的次數>插入和刪除,選擇AVL樹;搜尋,插入刪除次數幾乎差不多,選擇紅黑樹 - 問題2:紅黑樹插入刪除元素後如何改變元素顏色?
解決方案:
程式碼除錯中的問題和解決過程
- 問題1:PP11.3toString異常

解決方案:尚未解決
錯題分析
無測試
結對及互評
點評過的同學部落格和程式碼
- 本週結對學習情況
20172327 - 結對學習內容
•閱讀第11章節,執行教材上的程式碼
•完成程式設計專案PP10.3、PP11.8
•完成課後自測題,並參考答案學習
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 0/0 | 1/2 | 20/20 | |
| 第二週 | 328/328 | 1/3 | 20/40 | |
| 第三週 | 1597/ 1925 | 1/4 | 20/60 | |
| 第四周 | 1153/3850 | 1/5 | 20/80 | |
| 第五週 | 1583/5433 | 1/6 | 20/100 | |
| 第六週 | 1515/6948 | 1/7 | 20/120 |
