教材學習內容總結

概述

• 二叉查詢樹：是含附加屬性的二叉樹，即其左孩子小於父節點，而父節點又小於或等於右孩子。
• 二叉查詢樹的定義是二叉樹定義的擴充套件。
• 二叉查詢樹的各種操作
  

用連結串列實現二叉查詢樹

• 每個BinaryTreeNode物件要維護一個指向結點所儲存元素的引用，另外還要維護指向結點的每個孩子的引用。
• LinkedBinarySearchTree類提供兩個建構函式：一個負責建立一個空的LinkedBinarySearchTree；另一個負責建立一棵根結點為特定元素的LinkedBinarySearchTree。這兩個建構函式都只是引用了LinkedBinaryTree中相應的那兩個建構函式。
• addElement操作：就是根據給定元素的值，在樹中的恰當位置新增該元素。
  • 如果該元素不是Comparable，該方法會丟擲NoComparableElementException異常。
  • 如果樹為空，該元素稱為新結點。
  • 如果樹非空，則依據二叉查詢樹的性質，分別與某結點及其左右孩子比較，按照左孩子<父節點，父節點<=右孩子的規則將其新增到適當位置，或者稱為左右孩子的孩子。
  • 向二叉樹中新增元素
    
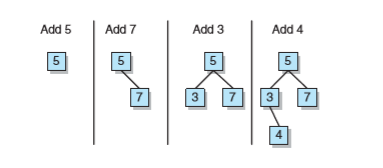
• removeElement操作：從二叉查詢樹中刪除一個元素時，必須推選出另一個結點（replacement方法找到這個結點）來代替要被刪除的那個結點。
  • 在樹中找不到給定目標元素時，丟擲ElementNotFoundException異常。
  • 選擇替換結點的三種情況
    • 被刪除結點沒有孩子，則replacement返回null
    • 被刪除結點只有一個孩子，replacement返回這個孩子
    • 被刪除結點有兩個孩子，replacement返回中序後繼者（因為相等元素會放到右邊）
  • 從二叉樹中刪除元素
    
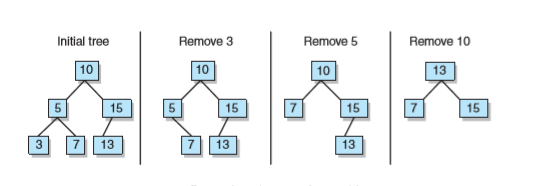
• removeAllOccurrences操作：從二叉查詢樹中刪除指定元素的所有存在。
  • 在樹中找不到給定目標元素時，丟擲ElementNotFoundException異常。
  • 如果該元素不是Comparable，該方法會丟擲ClassCastException異常。
  • 該方法會呼叫一次removeElement方法，以確保當樹中根本不存在指定元素時會丟擲異常。
  • 如果樹中還含有目標元素，就會再次呼叫removeElement方法。
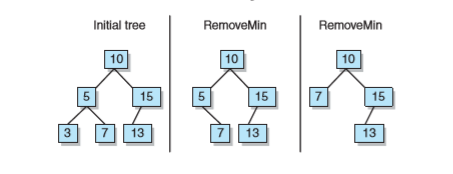
• removeMin操作：根據二叉查詢樹的定義，最右側存最大的結點，最左側存最小元素。
  • 如果樹根沒有左孩子，根結點為最小，右孩子變為新的根結點。
  • 如果左孩子是葉子結點，將父結點的引用設為null即可。
  • 如果左孩子是內部結點，則這個左孩子的右孩子將代替自己成為它父節點的左孩子。
    

有序列表實現二叉查詢樹

• 樹的主要使用之一就是為其它集合提供高效的實現。
• LinkedBinarySearchTree類的方法與有序列表的方法之間存在著一一對應的關係。

• 列表的一些常見操作
  

• 有序列表的特有操作
  

• BinarySearchTreeList實現的分析
  • BinarySearchTreeList的實現是一種帶有附加屬性（任何結點的最大深度為log2n，其中n為樹中儲存元素的個數）的平衡二叉查詢樹
  • 樹實現會使有些操作變得高效，有些操作變得低效
  • add操作和remove操作需要重新平衡化樹
  • 有序列表的連結串列實現分析和二叉查詢樹實現分析
    
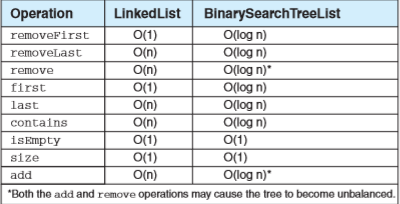
• 平衡二叉查詢樹

  • 如果二叉查詢樹不平衡，其效率可能比線性結構的還要低。例如蛻化樹看起來更像一個連結串列，事實上它的效率比連結串列的還低，因為每個結點附帶有額外的開銷。
    

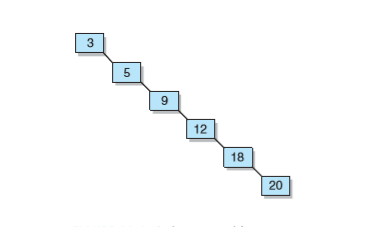
  • 如果沒有平衡假設，當樹根是樹中最小元素而被插入元素是樹中最大的元素時，這種情況下addElement操作的時間複雜性是O（n）而不是O（logn）。

  • 我們的目標是保持樹的最大路徑長度為（或接近）log2n。

平衡化樹的四種方法

• 自樹根向下的路徑最大長度不超過log2n，最小長度必須不小於log2（n-1）
• 平衡因子指左子樹減右子樹深度的值。
• 右旋
  • 通常是指左孩子繞著其父結點向右旋轉。是由於樹根的左孩子的左子樹中較長的路徑導致的不平衡。
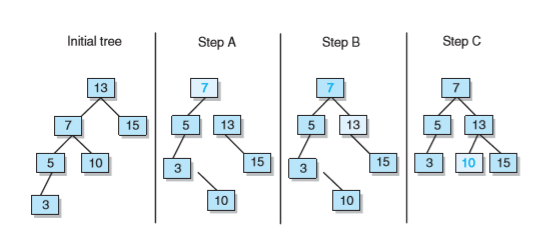
  • 如圖所示的初始樹，首先可以計算他成為平衡樹之後的樣子，他現在的最大路徑長度是3，最小路徑長度是1，樹中有6個元素，因此最大路徑長度應該是log26，即2。要平衡化該樹，需要三步
    • 使根的左孩子稱為新根
    • 使原來的根元素稱為新根的右孩子
    • 使原根的左孩子的右孩子成為原樹根的新的左孩子
  • 如圖是依據上面得三步的右旋過程
    
• 左旋
  • 通常指右孩子繞著其父結點向左旋轉。是由於較長的路徑出現在樹根右孩子的右子樹中而導致的不平衡。
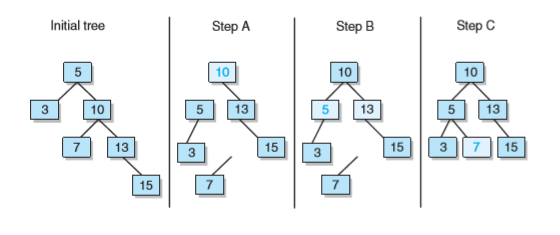
  • 同樣於右旋，為了平衡化，需要三步
    • 使樹根的右孩子元素成為新的根元素
    • 原根元素稱為新根元素的左孩子
    • 原樹根右孩子的左孩子成為原樹根新的右孩子
  • 如圖是依據上面的三步的左旋過程
    
• 右左旋
  • 對於由樹根右孩子的左子樹中較長路徑而導致的不平衡，需要先讓樹根右孩子的左孩子繞其父結點進行一次右旋，再讓樹根的右孩子繞樹根進行一次左旋。
  • 如圖
    
• 左右旋
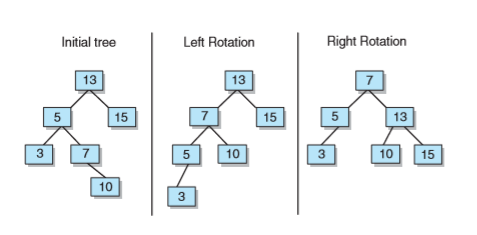
  • 對於由樹根左孩子的右子樹中較長路徑而導致的不平衡，需要先讓樹根左孩子的右孩子繞其父結點進行一次左旋，再讓樹根的左孩子繞樹根進行一次右旋。
    

實現二叉查詢樹：AVL樹

• 對於樹中任何結點，如果其|平衡因子|（右子樹的高度減去左子樹的高度）>1，那麼以該結點為樹根的子樹需要重新平衡。

• 樹（或樹的任何子樹）只有兩種途徑變得不平衡:插入結點或刪除結點。因此在每次進行這兩種操作時，都必須更新平衡因子，然後從插入或刪除結點的那個地方開始檢查樹的平衡性。上溯到根結點，所以AVL樹通常最好實現為每個結點都包含一個指向父結點的引用。

• AVL樹的右旋
  • 某結點的平衡因子為-2，則左子樹過長，如果左孩子的平衡因子是-1，則這個結點的左子樹為較長的路徑，將這個左孩子繞初始結點右旋一次即可平衡該樹。
    
• AVL樹的左旋
  • 某結點的平衡因子是+2，則右子樹過長，如果右孩子的平衡因子是+1,則意味著較長的路徑處在這個右孩子的右子樹中，將該右孩子繞初始結點進行一次左旋即可平衡。
• AVL樹的右左旋
  • 同樣根據平衡因子來判斷，某結點的平衡因子是+2,右孩子的平衡因子是-1，則過長的是右孩子的左子樹，需要進行一次右左雙旋（初始結點的右孩子的左孩子繞初始結點的右孩子進行一次右旋，再讓初始結點的右孩子繞初始結點進行一次左旋）如圖
    
• AVL樹的左右旋
  • 同樣根據平衡因子來判斷，某結點的平衡因子是-2,右孩子的平衡因子是+1，則過長的是左孩子的右子樹，需要進行一次左右雙旋（初始結點的左孩子的右孩子繞初始結點的左孩子進行一次左旋，再讓初始結點的左孩子繞初始結點進行一次右旋）

實現二叉查詢樹：紅黑樹

• 紅黑樹是一種平衡二叉查詢樹，其中的每個結點儲存一種顏色（紅色或黑色，用布林值表示，false表示紅色）。結點顏色的規則：
  • 根結點為黑色
  • 紅色結點的所有孩子都為黑色
  • 從樹根到樹葉的每條路徑都包含同樣數目的黑色結點
• 某種程度上，紅黑樹中的平衡限制沒有AVL樹那麼嚴格，但他們的序仍然是logn。
• 紅黑樹路徑中至多一半紅結點，至少一半黑結點。
• 紅黑樹最大高度約為2*logn，於是遍歷最長路徑的序仍然是logn。
• 插入的結點認為是紅色，空結點認為是黑色。

• 紅黑樹示意：
  

• 紅黑樹中的元素插入
  • 開始把新元素的顏色設定成紅色，然後重新平衡化該樹，根據紅黑樹的屬性改變元素顏色，最後總會把根結點設為黑色。
  • 插入之後的重新平衡化是一種迭代過程，從插入點上溯到樹根，迭代過程的終止條件有兩種
    • （current == root）：原因是每條路徑黑色元素相同，而根節點總為黑色。
    • （current.parent.color == black）：因為current所指向的每一個結點都是紅色（開始時，總是把新元素設定成紅色，那麼其父結點不可能為紅色），那麼如果當前結點的父結點是黑色，由於黑色數目是固定不變的，並且平衡時上溯處理早已平衡了當前結點的下面子樹，所以只要滿足這個條件，就可以實現平衡。
      在每次迭代的過程中，有以下情況：
    • 父結點是左孩子
      • 右叔叔是紅色
        • 父結點為黑
        • 右叔叔為黑
        • 祖父為紅
        • current由我變成父結點
          
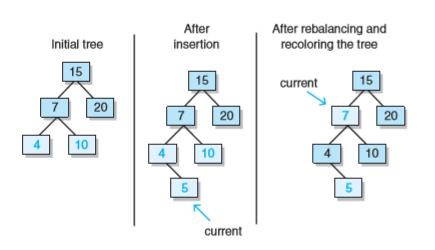
      • 右叔叔是黑色
        • 我是右孩子的情況下
          • current由我變成父結點
          • 繞current左旋，current變成左孩子
          • （current為左孩子的步驟）
          • 父結點為黑
          • 祖父為紅
          • 如果祖父不為空，讓父結點繞祖父右旋
    • 父結點是右孩子
      • 左叔叔是紅色
        • 父結點為黑
        • 左叔叔為黑
        • 祖父為紅
        • current由我變成祖父
          
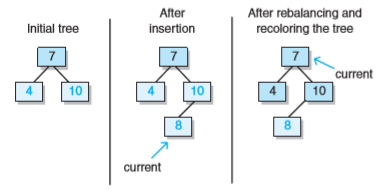
      • 左叔叔是黑色
        • 我是左孩子的情況下
          • current由我變成父結點
          • 繞current右旋，current變成右孩子
          • （current為右孩子的步驟）
          • 父結點為黑
          • 祖父為紅
          • 如果祖父不為空，讓父結點繞祖父左旋
    • 以上兩種情況是對稱的，並且最後都會把根結點變為黑色。插入中最關注的是叔叔的顏色。
• 紅黑樹中的元素刪除
  • 刪除元素之後需要重新平衡化（即重新著色），是一個迭代過程，終止條件有兩種：
    • （current == root）
    • （current.color == red）？？？？？？
    • 如果兄弟顏色是紅
      • 設定兄弟為黑
      • 父結點為紅
      • 兄弟繞父結點右旋
      • 舊兄弟絕交，新兄弟等於父結點的左孩子
        
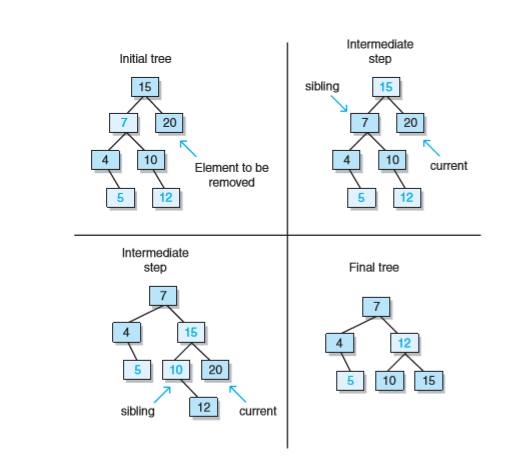
        接下來不管兄弟是黑還是紅都要進行的步驟：
    • 兄弟的兩個孩子都是black/null
      • 設定兄弟顏色是紅
      • current由我變為父結點
    • 兄弟的兩個孩子不全為黑
      • 左孩子為黑
        • 兄弟的右孩子為黑
        • 兄弟為紅
        • 讓兄弟的右孩子繞兄弟右旋
        • 兄弟等於父結點的左孩子
    • 兄弟的兩個孩子都不為黑
      • 兄弟為父結點的顏色
      • 父結點為黑
      • 兄弟左孩子顏色為黑
      • 兄弟繞父結點右旋
      • current由我變為樹根
    • 迴圈結束後刪除該結點，並設定父親的孩子引用為null。刪除中最關注的是兄弟的顏色。

教材學習中的問題和解決過程

• 問題一：在紅黑樹的刪除中，迭代的一個終止條件是（current.color == red），不能理解原因。
• 問題一解決：由於每條路徑黑結點的個數是一樣的，當前結點為紅色時，滿足迭代條件，直到最後當前結點為紅時，滿足所有紅黑樹的規則。
• 問題二：removeElement操作的程式碼理解有問題

• 問題二解決：

  public T removeElement(T targetElement) {
      T result = null;
      if (isEmpty()) {//樹為空時丟擲異常
          throw new ElementNotFoundException("LinkedbinarySearchTree");
      } else {//樹不為空
          BinaryTreeNode<T> parent = null;
          if (((Comparable<T>) targetElement).equals(root.getElement())) {//要刪除的元素是根結點
              result = root.element;
              BinaryTreeNode<T> temp = replacement(root);
              if (temp == null) {//找不到結點替換
                  root = null;
              } else {
              //用找到的結點替換根結點
                  root.element = temp.element;
                  root.setLeft(temp.getLeft());
                  root.setRight(temp.getRight());
              }
              modCount--;
          } else {//要刪除根節點的孩子
              parent = root;
              if (((Comparable<T>) targetElement)
                      .compareTo(root.getElement()) < 0) {//目標在根的左邊
                  result = removeElement(targetElement, root.getLeft(),
                          parent);
              } else {//目標在根的右邊
                  result = removeElement(targetElement, root.getRight(),
                          parent);
              }
          }
      }
      return result;
  }
  private T removeElement(T targetElement, BinaryTreeNode<T> node,
                          BinaryTreeNode<T> parent) {//用來刪除除根以外的目標元素
      T result = null;
      if (node == null) {
          throw new ElementNotFoundException("LinkedbinarySearchTree");
      } else {
          if (((Comparable<T>) targetElement).equals(node.getElement())) {//找到目標元素
              result = node.element;
              BinaryTreeNode<T> temp = replacement(node);//將node元素刪除
              //往下繼續查詢目標元素，看看左右孩子是否是
              if (parent.right == node) {
                  parent.right = temp;
              } else {
                  parent.left = temp;
              }
              modCount--;
          } else {//如果目標元素比根結點小，則在根結點左側，再次使用該方法從左子樹中查詢目標元素
              parent = node;
              if (((Comparable<T>) targetElement)
                      .compareTo(root.getElement()) < 0) {
                  result = removeElement(targetElement, root.getLeft(),
                          parent);
              } else {//目標元素比根結點大，再次使用該方法從右子樹中查詢目標元素
                  result = removeElement(targetElement, root.getRight(),
                          parent);
              }
          }
      }
      return result;
  }
  // 刪除元素
  private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node) {
      BinaryTreeNode<T> result = null;
      if ((node.left == null) && (node.right == null)) {//如果左右子樹都為空，該元素沒有孩子，直接返回空刪掉它即可
          result = null;
      } else if ((node.left != null) && (node.right == null)) {只有左孩子時，將父結點指向左孩子
          result = node.left;
      } else if ((node.left == null) && (node.right != null)) {//只有右孩子時，將父結點指向右孩子
          result = node.right;
      } else {/* 先找到其右子樹的最左孩子（或者左子樹的最右孩子），即左（右）子樹中序遍歷時的第一個節點，然後將其與待刪除的節點互換，最後再刪除該節點（如果有右子樹，則右子樹上位）。總之就是先找到它的替代者，找到之後替換這個要刪除的節點，然後再把這個節點真正刪除掉。*/
          BinaryTreeNode<T> current = node.right;//初始化右側第一個結點
          BinaryTreeNode<T> parent = node;
          //獲取右邊子樹的最左邊的結點
          while (current.left != null) {
              parent = current;
              current = current.left;
          }
          current.left = node.left;
          // 如果當前待查詢的結點
          if (node.right != current) {
              parent.left = current.right;// 整體的樹結構移動就可以了
              current.right = node.right;
          }
          result = current;
      }
      return result;
  }

• 問題三：對於removeElement方法中“若被刪除結點有兩個孩子，replacement返回中序後繼者”一句不能理解返回的是哪個結點

• 問題三解決：在課堂上，老師提到了前驅結點，就是對一棵樹進行中序排序，形成一個序列，書上所提到的返回中序後繼者的意思就是排序後的序列的被刪除結點的前驅結點或後驅結點都可以，由自己來定義。例如
  

  對這棵樹進行中序排序為：2 3 4 5 6。刪除結點3後，可以返回前驅結點2，也可以返回後驅結點4。