目錄

1、MOEA/D的特點

2、 MOEA/D的分解策略

3、MOEA/D的流程

基於分解的多目標進化演算法（Multi-objectiveEvolutionary Algorithm Based on Decomposition, MOEA/D）將多目標優化問題被轉化為一系列單目標優化子問題，然後利用一定數量相鄰問題的資訊，採用進化演算法對這些子問題同時進行優化。因為Pareto前沿面上的一個解對應於每一個單目標優化子問題的最優解，最終可以求得一組Pareto最優解。由於分解操作的存在，該方法在保持解的分佈性方面有著很大優勢，而通過分析相鄰問題的資訊來優化，能避免陷入區域性最優。

1、MOEA/D的特點

與其它多目標進化演算法相比，MOEA/D具有以下特點：

(1) MOEA/D將分解引入到多目標進化計算中，使得分解的方法可以真正的被併入到進化演算法中，通過使用MOEA/D框架來解決多目標優化問題。 

(2)因為MOEA/D演算法是同時優化N標量子問題而不是直接將多目標優化問題作為一個整體來解決，那麼MOEA/D將會降低傳統MOEA的多樣性保持和適應度分配的難度。 

(3)MOEA/D利用相鄰子問題的解的資訊去同時優化N標量子問題。相對來說，MOEA/D不會重複的優化標量子問題，因為它利用了子問題之間的協同進化機制，所以演算法的計算複雜度比較低。

(4)可以將目標歸一化技術納入MOEA / D以處理不同比例的目標。因為在實際問題當中，一定數量的目標函式的值之間的差距會非常大，不能簡單地直接將它們進行聚合。

2、 MOEA/D的分解策略

多目標優化問題（MOP）：  

                                             subject to 

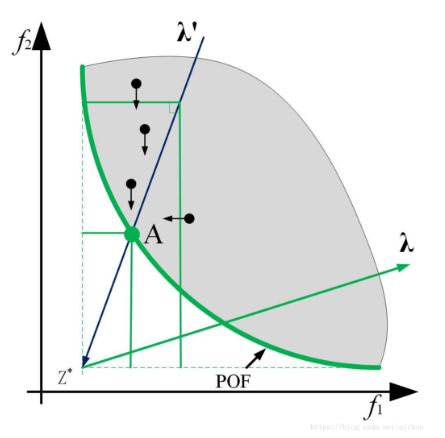
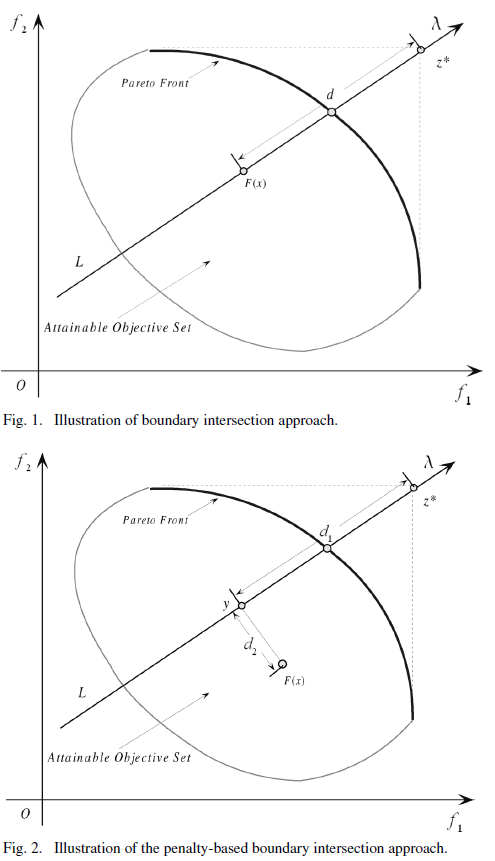
注意：下圖為最小化問題情況 

注意：下圖為最小化問題情況  

3、MOEA/D的流程

在下面的描述中，我們使用Tchebycheff的分解法。對於定義下面MOEA/D演算法，使用別的分解方法影響很小。 

令為一組均勻分佈的權重向量，為參考點。對PF的逼近問題可以通過Tchebycheff法分解為N個標量優化子問題，其中每個子問題可表示為：     

其中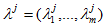。在單次執行中，MOEA/D會同時優化這N個目標函式。 

在MOEA/D中，權重向量的鄰居取 中的幾個與之最接近的權重向量。每一代種群都是由各個子問題的當前最優解所構成的集合。在MOEA/D中，只有相鄰的子問題可以被用來優化彼此。

對於第t代種群，使用Tchebycheff法的MOEA/D包含以下初始條件：

① 大小為N的種群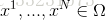，，其中是第i個子問題的當前最優解。

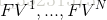
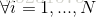
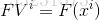
② ，其中對於，。

③ ，是目前搜尋到的目標函式的最優值。

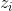
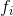
④ 外部種群(EP)，用來儲存目前演算法搜尋到的最優解。