最好,最壞,平均,均攤時間複雜度
// n 表示陣列 array 的長度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) pos = i;
}
return pos;
}
時間複雜度是O(n)
// n 表示陣列 array 的長度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
最好是O(1),最壞是O(n)
平均時間複雜度如圖:
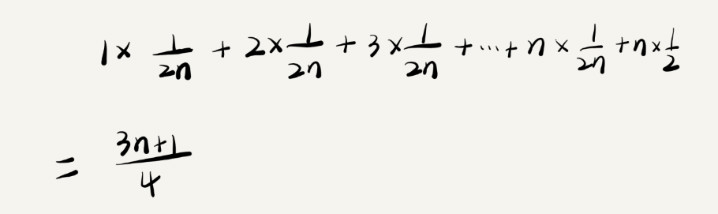
相關推薦
算法系列-複雜度分析:淺析最好、最壞、平均、均攤時間複雜度
整理自極客時間-資料結構與演算法之美。原文內容更完整具體,且有音訊。購買地址: 上一節,我們講了複雜度的大 O 表示法和幾個分析技巧,還舉了一些常見覆雜度分析的例子,比如 O(1)、O(logn)、O(n)、O(nlogn) 複雜度分析。掌握了這些內容,對於複雜度分析這個知識點,你已經
【資料結構與演算法-java實現】二 複雜度分析(下):最好、最壞、平均、均攤時間複雜度的概念
上一篇文章學習了:如何分析、統計演算法的執行效率和資源消耗? 點選連結檢視上一篇文章:複雜度分析上 今天的文章學習以下內容: 最好情況時間複雜度 最壞情況時間複雜度 平均情況時間複雜度 均攤時間複雜度 1、最好與最壞情況時間複雜度 我們首先
04-演算法複雜度分析(下):最好、最壞、平均、均攤時間複雜度
上一節,我們講了複雜度的大 O 表示法和幾個分析技巧,還舉了一些常見覆雜度分析的例子,比如 O(1)、O(logn)、O(n)、O(nlogn) 複雜度分析。掌握了這些內容,對於複雜度分析這個知識點,你已經可以到及格線了。但是,我想你肯定不會滿足於此。 今天我會
3L-最好、最壞、平均、均攤時間複雜度
> 關注公眾號 MageByte,設定星標點「在看」是我們創造好文的動力。後臺回覆 “加群” 進入技術交流群獲更多技術成長。 本文來自 MageByte-青葉編寫 上次我們說過 [時間複雜度與空間復度](https://mp.weixin.qq.com/s/2yDJjVJC4N404g7ISmvAzw
最好,最壞,平均,均攤時間複雜度
// n 表示陣列 array 的長度int find(int[] array, int n, int x) { int i = 0; int pos = -1; for (; i < n; ++i) { if (array[i]
Chapter4 複雜度分析(下):淺析最好,最壞,平均,均攤時間複雜度
四個複雜度分析: 1:最好情況時間複雜度(best case time complexity) 2:最壞情況時間複雜度(worst case time complexity) 3:平均情況時間複雜度(average case time complexity) 4:均攤時間複雜度(amortized t
均攤時間複雜度與複雜度震盪
前言 我們平常分析複雜度一般是分析一個演算法從頭執行到尾它的複雜度是怎樣的。但我們在專案中經常會寫一個複雜度較高的演算法,但是這個高複雜度的演算法是為了方便其他操作。此時我們通常會將這個複雜度較高的演算法和其他的操作放在一起來分析複雜度。這個複雜度較高的演算法複雜度將會均攤到其他的操作中
定義棧的資料結構,請在該型別中實現一個能夠得到棧中所含最小元素的min函式(時間複雜度應為O(1))。
import java.util.Stack; public class Solution { private Stack<Integer> min_stack=new Stack<Integer>(); private Stack<Integer&
定義棧的資料結構,請在該型別中實現一個能夠得到棧中所含最小元素的min函式(時間複雜度應為O(1))
/** 思路:利用兩個棧來實現,一個主棧正常壓棧出棧,一個輔助棧用來儲存主棧所有值的最小值, 壓棧時,當壓入的值比輔助棧棧頂值大時,主棧正常壓棧,輔助棧不壓棧,小於等於二者都壓棧; 出棧時,當主棧和輔助棧棧頂元素不相等時,主棧正常出棧,輔助棧不出棧。 */ class Sol
定義棧的資料結構,請在該型別中實現一個能夠得到棧中所含最小元素的min函式 (時間複雜度應為O(1))。
import java.util.Stack; /** * 定義棧的資料結構,請在該型別中實現一個能夠得到棧中所含最小元素的min函式 * (時間複雜度應為O(1))。 */ public class Solution { static Stack<Integer> da
【面試題】實現一個棧,要求Push(入棧),Pop(出棧),Min(返回最小值的操作)的時間複雜度為O(1)
問題描述:實現一個棧,要求Push(入棧),Pop(出棧),Min(返回最小值的操作)的時間複雜度為O(1) 分析問題:要記錄從當前棧頂到棧底元素的最小值,很容易想到用一個變數,每push一個元素更新一次變數的值。那麼問題來了,當執行pop操作時,上一次的最小值就找不到
【資料結構】實現一個棧,要求實現Push(出棧)、Pop(入棧)、Min(返回最小值的操作)的時間複雜度為O(1)
實現一個棧,要求實現Push(出棧)、Pop(入棧)、Min(返回最小值的操作)的時間複雜度為O(1) 在棧中操作的話,push和pop的時間複雜度就是O(1),所以我們只用實現Min(返回最小值的操作)的時間複雜度為O(1), 思想就是用兩個棧,一個就是普通的存取資料的
實現一個棧Stack,要求實現Push(出棧)、Pop(入棧)、 Min(返回最小值的操作)的時間複雜度為O(1)
利用兩個棧 1. 一個用來儲存最小的元素 smin 2. 一個用來儲存所有元素 scur 3. 入棧時,scur直接壓入,smin棧頂與目標元素比較,若小之則壓入,否則不做處理 4. 出棧時,s
定義棧的資料結構,請在該型別中實現一個能夠得到棧最小元素的min函式。時間複雜度都是O(1)
定義棧的資料結構,請在該型別中實現一個能夠得到棧最小元素的min函式。要求:使得時間複雜度都是O(1) 完成如下的函式: import java.util.Stack; public class Solution { public void pus
實現一個棧Stack,要求實現Push(出棧)、Pop(入棧)、Min(返回最小值的操作)的時間複雜度為O(1)
這裡的要求呢,跟我們平時的stack操作是一樣的,那什麼地方不同呢?多了一個min方法,並且要求時間複雜度為O(1),那該怎麼做呢?O(1)的意思就是說,要用了,直接就能拿到,就好比陣列直到下標一樣,直接取。 那麼如果能夠將一個棧的棧頂一直存放的都是最小值呢?
【棧佇列】實現一個棧Stack,要求實現Push(出棧)、Pop(入棧)、Min(返回最小值的操作)的時間複雜度為O(1)
問題分析 要記錄從當前棧頂到棧底元素的最小值,很容易想到用一個變數,每push一個元素更新一次變數的值。那麼問題來了,當執行pop操作時,上一次的最小值就找不到了。 解決方法 方法1、 使用一個棧。元素x入棧時,執行一次push(x),再push(min
騰訊面試題:模板實現一個棧,要求Push(入棧),Pop(出棧),Max(返回最大值的操作)的時間複雜度為O(1)
解題思路:要用模板實現亂序入棧的陣列每次pop()出棧都能得到當前棧中Max的最大值,就必須在push()入棧時進行維護操作,使的每次入棧的元素都能夠找到合適的位置並push(),每次push()操作完成後棧中的元素都能夠按從棧頂到棧底從大到小排列即可。這就需要寫一個不同於常
定義棧的資料結構,請在該型別中實現一個能夠得到棧中所含最小元素的min函式(時間複雜度應為
import java.util.Stack; //個人認為這種方式有問題,假設把最小值出棧,再求最小值就有問題 public c
設計一個堆疊,函式min、push 以及pop 的時間複雜度都是O(1)
/** * 2.設計包含min 函式的棧。 * 定義棧的資料結構,要求新增一個min 函式,能夠得到棧的最小元素。 * 要求函式min、push 以及pop 的時間複雜度都是O(1)。 * * 經典的空間換取時間,這個是利用java語言的JDK的實現的
最長遞增子序列優化演算法(時間複雜度為nlgn)C++實現
最長遞增子序列優化演算法(時間複雜度為nlgn) // 最長遞增子序列優化演算法.cpp : Defines the entry point for the console application. /
