簡介

本文受 淺析 Hinton 最近提出的 Capsule 計劃 啟發，希望以更通俗的方式推廣機器學習演算法，讓有數學基礎和程式設計能力的人能夠樂享其中。

目前人工智慧和深度學習越趨普及，大家可以使用開源的Scikit-learn、TensorFlow來實現機器學習模型，甚至參加Kaggle這樣的建模比賽。那麼要想模型效果好，手動調參少不了，機器學習演算法如SVM就有gamma、kernel、ceof等超引數要調，而神經網路模型有learning_rate、optimizer、L1/L2 normalization等更多超引數可以調優。

很多paper使用一個新的模型可以取得state of the art的效果，然後提供一組超引數組合方便讀者復現效果，實際上這些超引數都是“精挑細選”得到的，背後有太多效果不好的超引數嘗試過程被忽略，大家也不知道對方的超引數是如何tune出來的。因此，瞭解和掌握更好的超引數調優方法在科研和工程上是很有價值的，本文將介紹一種更好的超引數調優方式，也就是貝葉斯優化（Bayesian Optimization），以及開源調參服務Advisor的使用介紹。

超引數介紹

首先，什麼是超引數（Hyper-parameter）？這是相對於模型的引數而言（Parameter），我們知道機器學習其實就是機器通過某種演算法學習資料的計算過程，通過學習得到的模型本質上是一些列數字，如樹模型每個節點上判斷屬於左右子樹的一個數，或者邏輯迴歸模型裡的一維陣列，這些都稱為模型的引數。

那麼定義模型屬性或者定義訓練過程的引數，我們稱為超引數，例如我們定義一個神經網路模型有9527層網路並且都用RELU作為啟用函式，這個9527層和RELU啟用函式就是一組超引數，又例如我們定義這個模型使用RMSProp優化演算法和learning rate為0.01，那麼這兩個控制訓練過程的屬性也是超引數。

顯然，超引數的選擇對模型最終的效果有極大的影響。如複雜的模型可能有更好的表達能力來處理不同類別的資料，但也可能因為層數太多導致梯度消失無法訓練，又如learning rate過大可能導致收斂效果差，過小又可能收斂速度過慢。

那麼如何選擇合適的超引數呢，不同模型會有不同的最優超引數組合，找到這組最優超引數大家會根據經驗、或者隨機的方法來嘗試，這也是為什麼現在的深度學習工程師也被戲稱為“調參工程師”。根據No Free Lunch原理，不存在一組完美的超引數適合所有模型，那麼調參看起來是一個工程問題，有可能用數學或者機器學習模型來解決模型本身超引數的選擇問題嗎？答案顯然是有的，而且通過一些數學證明，我們使用演算法“很有可能”取得比常用方法更好的效果，為什麼是“很有可能”，因為這裡沒有絕對只有概率分佈，也就是後面會介紹到的貝葉斯優化。

自動調參演算法

說到自動調參演算法，大家可能已經知道了Grid search（網格搜尋）、Random search（隨機搜尋），還有Genetic algorithm（遺傳演算法）、Paticle Swarm Optimization（粒子群優化）、Bayesian Optimization（貝葉斯優化）、TPE、SMAC等。

這裡補充一個背景，機器學習模型超引數調優一般認為是一個黑盒優化問題，所謂黑盒問題就是我們在調優的過程中只看到模型的輸入和輸出，不能獲取模型訓練過程的梯度資訊，也不能假設模型超引數和最終指標符合凸優化條件，否則的話我們通過求導或者凸優化方法就可以求導最優解，不需要使用這些黑盒優化演算法，而實際上大部分的模型超引數也符合這個場景。其次是模型的訓練過程是相對expensive的，不能通過快速計算獲取大量樣本，我們知道DeepMind用增強學習模型DQN來打Atari遊戲，實際上每一個action操作後都能迅速取得當前的score，這樣收集到大量樣本才可以訓練複雜的神經網路模型，雖說我們也可以用增強學習來訓練超引數調優的模型，但實際上一組超引數要訓練一個模型需要幾分鐘、幾小時、幾天甚至幾個月的時間，無法快速獲取這麼多樣本資料，因此需要有更“準確和高效”的方法來調優超引數。

像遺傳演算法和PSO這些經典黑盒優化演算法，我歸類為群體優化演算法，也不是特別適合模型超引數調優場景，因為需要有足夠多的初始樣本點，並且優化效率不是特別高，本文也不再詳細敘述。

目前業界用得比較多的分別是Grid search、Random search和Bayesian Optimization。網格搜尋很容易理解和實現，例如我們的超引數A有2種選擇，超引數B有3種選擇，超引數C有5種選擇，那麼我們所有的超引數組合就有2 * 3 * 5也就是30種，我們需要遍歷這30種組合並且找到其中最優的方案，對於連續值我們還需要等間距取樣。實際上這30種組合不一定取得全域性最優解，而且計算量很大很容易組合爆炸，並不是一種高效的引數調優方法。

業界公認的Random search效果會比Grid search好，Random search其實就是隨機搜尋，例如前面的場景A有2種選擇、B有3種、C有5種、連續值隨機取樣，那麼每次分別在A、B、C中隨機取值組合成新的超引數組合來訓練。雖然有隨機因素，但隨機搜尋可能出現效果特別差、也可能出現效果特別好，在嘗試次數和Grid search相同的情況下一般最值會更大，當然variance也更大但這不影響最終結果。在實現Random search時可以優化，過濾隨機可能出現過的超引數組合，不需要重複計算。

實際上Grid search和Random search都是非常普通和效果一般的方法，在計算資源有限的情況下不一定比建模工程師的個人經驗要好，接下來介紹的Bayesian Optimization就是“很可能”比普通開發者或者建模工程師調參能力更好的演算法。首先貝葉斯優化當然用到了貝葉斯公式，這裡不作詳細證明了，它要求已經存在幾個樣本點（同樣存在冷啟動問題，後面介紹解決方案），並且通過高斯過程迴歸（假設超引數間符合聯合高斯分佈）計算前面n個點的後驗概率分佈，得到每一個超引數在每一個取值點的期望均值和方差，其中均值代表這個點最終的期望效果，均值越大表示模型最終指標越大，方差表示這個點的效果不確定性，方差越大表示這個點不確定是否可能取得最大值非常值得去探索。因此實現貝葉斯優化第一步就是實現高斯過程迴歸演算法，並且這裡可以通過類似SVM的kernel trick來優化計算，在後面的開源專案Advisor介紹中我們就使用Scikit-learn提供的GaussianProgressRegressor，最終效果如下圖，在只有3個初始樣本的情況下我們（通過100000個點的取樣）計算出每個點的均值和方差。

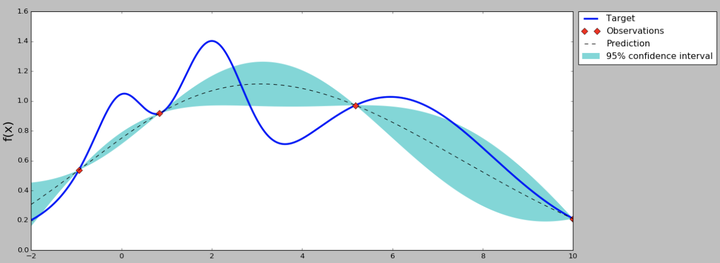
從曲線可以看出，中間的點均值較大，而且方差也比較大，很有可能這個點的超引數可以訓練得到一個效果指標好的模型。那為什麼要選均值大和方差大的點呢？因為前面提到均值代表期望的最終結果，當然是越大越好，但我們不能每次都挑選均值最大的，因為有的點方差很大也有可能存在全域性最優解，因此選擇均值大的點我們成為exploritation（開發），選擇方差大的點我們稱為exploration（探索）。那麼究竟什麼時候開發什麼時候探索，並且開發和探索各佔多少比例呢？不同的場景其實是可以有不同的策略的，例如我們的模型訓練非常慢，只能再跑1組超引數了，那應該選擇均值較大的比較有把握，如果我們計算力還能可以跑1000次，那麼就不能放棄探索的機會應該選擇方差大的，而至於均值和方差比例如何把握，這就是我們要定義的acquisition function了。acquisition function是一個權衡exploritation和exploration的函式，最簡單的acquisition function就是均值加上n倍方差（Upper condence bound演算法），這個n可以是整數、小數或者是正數、負數，更復雜的acquisition function還有Expected improvement、Entropy search等等。在原來的圖上加上acquisition function曲線，然後我們求得acquisition function的最大值，這是的引數值就是貝葉斯優化演算法推薦的超引數值，是根據超引數間的聯合概率分佈求出來、並且均衡了開發和探索後得到的結果。

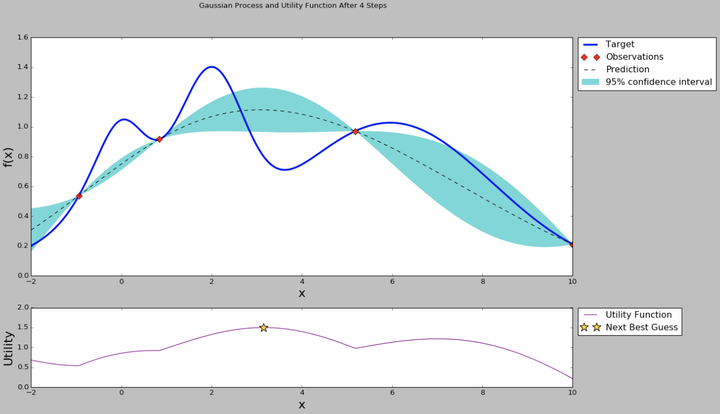
因此如果我們使用貝葉斯優化，那麼我們下一個點就取中間偏左的點，使用這個點代表的超引數來訓練模型，並且得到這個模型在這住超引數組合下的效果指標。有了新的指標，貝葉斯優化模型的樣本就從3個變成了4個，這樣可以重新計算超引數之間的後驗概率分佈和acquisition function，效果如下圖。

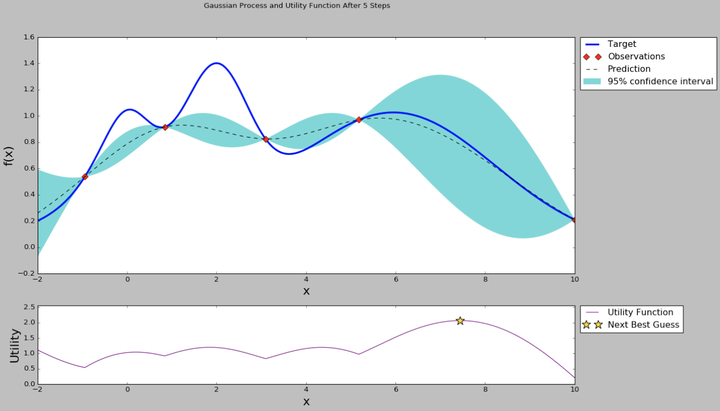
從均值和方差曲線看出，目前右邊的點均值不低，並且方差是比較大，直觀上我們認為探索右邊區域的超引數是“很可能”有價值的。從acquisition function曲線我們也可以看出，右邊的點在考慮了開發和探索的情況下有更高的值，因此我們下一個超引數推薦就是右邊星號的點。然後我們使用推薦的超引數繼續訓練，得到新的模型效果指標，加入到高斯過程迴歸模型裡面，得到新的均值-方差曲線和acquisition function曲線。

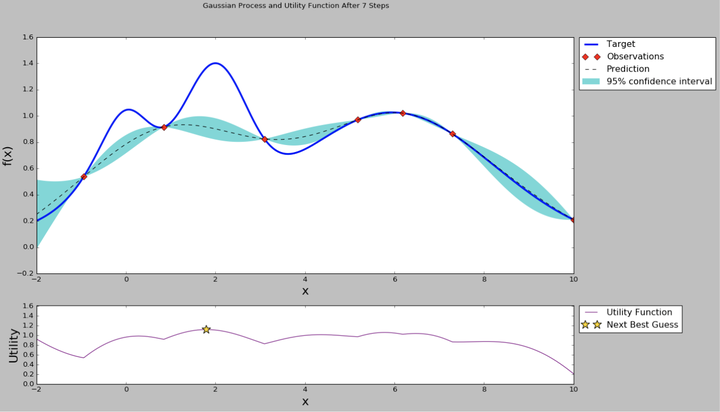
通過不斷重複上述的步驟，我們的曲線在樣本極少的情況下也可以畢竟最終真實的曲線。當然上面的圖是在一個黑盒優化問題上模擬的，因此我們知道真實的曲線形狀，現實的機器學習模型的超引數間不一定能畫出完整的曲線，但通過符合聯合高斯概率分佈的假設，還有高斯過程迴歸、貝葉斯方程等數學證明，我們可以從概率上找到一個“很可能”更好的超引數，這是比Grid search或者Random search更有價值的方法。

注意，前面提到的Bayesian Optimization等超引數優化演算法也是有超引數的，或者稱為超超引數，如acquisition function的選擇就是可能影響超引數調優模型的效果，但一般而言這些演算法的超超引數極少甚至無須調參，大家選擇業界公認效果比較好的方案即可。

Google Vizier

前面已經介紹了Grid search、Random search和Bayesian Optimization等演算法，但並不沒有完，因為我們要使用這些自動調參演算法不可能都重新實現一遍，我們應該關注於自身的機器學習模型實現而直接使用開源或者易用的調參服務。

近期Google就開放了內部調參系統Google Vizier的論文介紹，感興趣可以在這裡閱讀paper https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/46180.pdf

與開源的hyperopt、optunity不同，Vizier是一個service而不是一個library，也就是演算法開發者不需要自己部署調參服務或者管理引數儲存，只需要選擇合適的調參演算法，如貝葉斯優化，然後Vizier就會根據模型的一些歷史指標推薦最優的超引數組合給開發者，直接使用這些超引數會比自己瞎猜或者遍歷引數組合得到的效果更好。當然開發者可以使用Vizier提供的Algorithm Playground功能實現自己的自動調參演算法，還有內建一些EarlyStopAlgorithm也可以提前發現一些“沒有前途”的調優任務提前結束剩下計算資源。

目前Google Vizier已經支援Grid search、Random search已經改良過的Bayesian optimization，為什麼是改良過的呢？前面提到貝葉斯優化也需要幾個初始樣本點，這些樣本點一般通過隨機搜尋要產生，這就有冷啟動的代價了，Google將不同模型的引數都歸一化進行統一編碼，每個任務計算的GaussianProcessRegressor與上一個任務的GaussianProcessRegressor計算的殘差作為目標來訓練，對應的acquisition function也不是簡單的均值乘以n倍方差了，這相當於用了遷移學習模型的概念，從paper的效果看基本解決了冷啟動的問題，這個模型被稱為（Stacked）Batch Gaussian Process Bandit。

Google Vizier除了實現很好的引數推薦演算法，還定義了Study、Trial、Algorithm等非常好的領域抽象，這套系統也直接應用到Google CloudML的HyperTune subsystem中，開發者只需要寫一個JSON配置檔案就可以在Google Cloud上自動並行多工調參了。

Advisor開源專案

Google Vizier是目前我看過最讚的超引數自動調優服務，可惜的是它並沒有開源，外部也只有通過Google CloudML提交的任務可以使用其介面，不過其合理的基礎架構讓我們也可以重現一個類似的自動調參服務。

Advisor就是一個Google Vizier的開源實現，不僅實現了和Vizier完全一致的Study、Trial、Algorithm領域抽象，還提供Grid search、Random search和Bayesian optimization等演算法實現。使用Advisor很簡單，我們提供了API、SDK、Web以及命令列等多種訪問方式，並且已經整合Scikit-learn、XGBoost和TensorFlow等開源機器學習框架，基本只要寫一個Python函式定義好模型輸入和指標就可以實現任意的超引數調優（黑盒優化）功能。

Advisor使用Python實現，基於Scikit-learn的GPR實現了貝葉斯優化等演算法，也歡迎更多開發者參與，開源地址 tobegit3hub/advisor 。

Advisor線上服務

hypertune.cn 是我們提供的線上超引數推薦服務，也是體驗Advisor調參服務的最好入口，在網頁上我們就可以使用所有的Grid search、Random search、Bayesian optimization等演算法功能了。

首先開啟 http://hypertune.cn ， 目前我們已經支援使用Github賬號登入，由於還沒有多租戶許可權隔離因此不需要登入也可以訪問全域性資訊。在首頁我們可以檢視所有的Study，也就是每一個模型訓練任務的資訊，也可以在瀏覽器上直接建立Study。

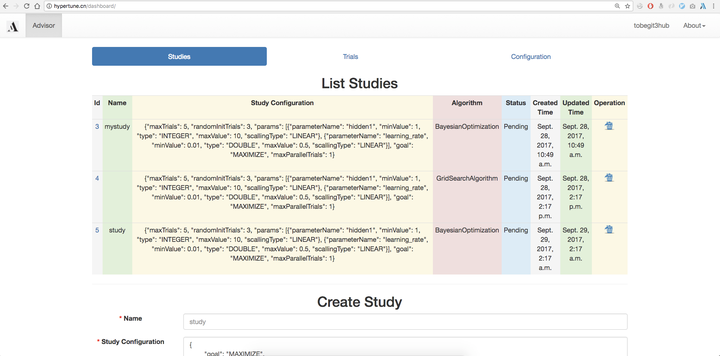
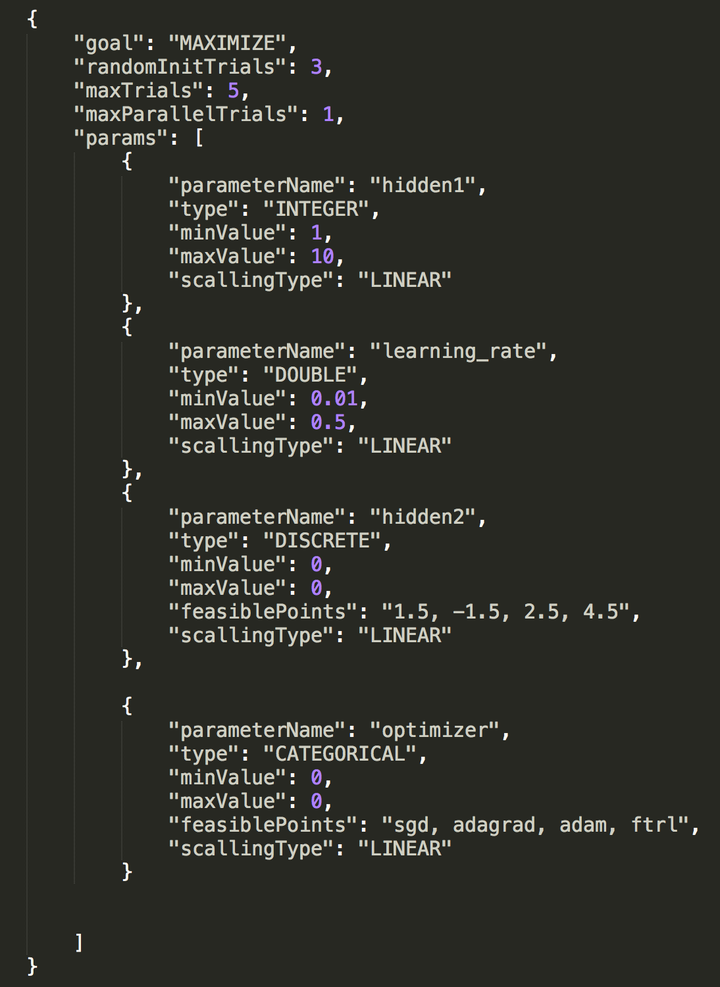
這裡需要使用者定義Study configuration，也就是模型超引數的search space，和Google Vizier一樣我們支援Double、Integer、Discrete和Categorical四種類型的超引數定義，基本涵蓋了數值型、字串、連續型以及離散型的任意超引數類別，更詳細的例子如下圖。

定義好Study好，我們可以進入Study詳情頁，直接點選“Generate Suggestions”按鈕生成推薦的超引數組合，這會根據使用者建立Study選擇的調參演算法（如BayesianOptimization）來推薦，底層就是基於Scikit-learn實現的聯合高斯分佈、高斯過程迴歸、核技巧、貝葉斯優化等演算法實現。

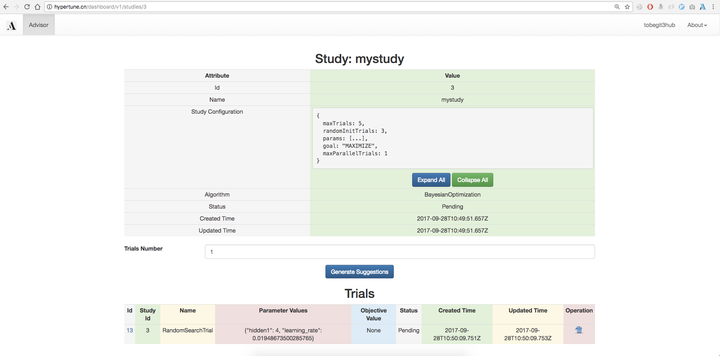
當然我們也可以使用Grid search、Random search等樸素的搜尋演算法，生成的Trial就是使用的該超引數組合的一次執行，預設是沒有objective value的，我們可以在外部使用該超引數進行模型訓練，然後把auc、accuracy、mean square error等指標在網頁上回填到引數推薦服務，下一次超引數推薦就會基於已經訓練得到模型資料，進行更優化、權衡exploritation和exploration後的演算法推薦。對於Eearly stop演算法，我們還需要每一步的效能指標，因此使用者可以提供Training step以及對應的Objective value，進行更細化的優化。

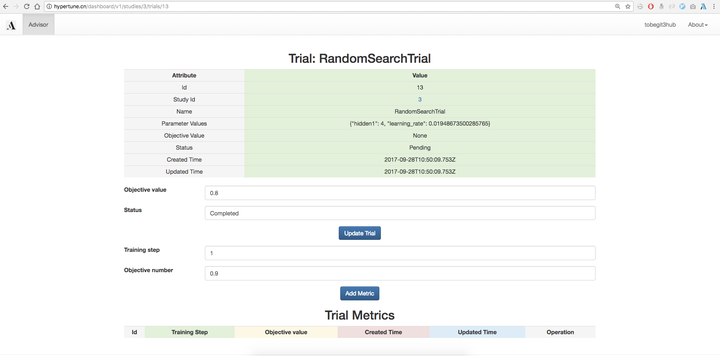
除了提供在網頁上整合推薦演算法，我們也集成了Scikit-learn、XGBoost和TensorFlow等框架，在命令列只要定義一個函式就可以自動實現建立Study、獲取Trial以及更新Trial metrics等功能，參考 https://github.com/tobegit3hub/advisor/tree/master/examples 。對於貝葉斯優化演算法，我們還提供了一維特徵的視覺化工具，像上面的圖一樣直觀地感受均值、方差、acquisition function的變化，參考 https://github.com/tobegit3hub/advisor/tree/master/visualization 。

總結

本文介紹了一種更好的超引數調優方法，也就是貝葉斯優化演算法，並且介紹了Google內部的Vizier調參服務以及其開源實現Advisor專案。通過使用更好的模型和工具，可以輔助機器學習工程師的建模流程，在學術界和工業界取得更多、更大的突破。

如果你有更好的超引數推薦演算法，不妨留言，我們有能力實現並且讓更多人用上 :)