返回整數陣列的最大子陣列的和
阿新 • • 發佈:2018-11-04
#include<iostream>
using namespace std;
int max(int a, int b)
{
if (a > b)
{
return a;
}
else
{
return b;
}
}
int main()
{
int Array[10000];
int i = 1,k;
int dynamic_planning[10000][2], j, sum[10000];
int start[10000] = {0};
int end[10000] = { 0 };
cout << "請輸入陣列:" << endl;
cin >> Array[0];
while (cin.get() != '\n')
{
cin >> Array[i++];
}
for (j = i; j < 2 * i; j++)
{
Array[j] = Array[j - i];
}
int n = 0;
while (true){
dynamic_planning[0][0] = 0;
dynamic_planning[0][1] = Array[n];
for (j = 1; j<i; j++)
{
dynamic_planning[j][0] = max(dynamic_planning[j - 1][0], dynamic_planning[j - 1][1]);
dynamic_planning[j][1] = max(Array[j+n], (dynamic_planning[j - 1][1] + Array[j+n]));
if (dynamic_planning[j - 1][1] < dynamic_planning[j][1] && dynamic_planning[j - 1][1]<0 && dynamic_planning[j][0] <= dynamic_planning[j][1])
{
start[n] = j+n;
}
if (dynamic_planning[j - 1][1] >= dynamic_planning[j][0])
{
end[n] = j-1+n;
}
if (dynamic_planning[j][1] >= dynamic_planning[j][0])
{
end[n] = j+n;
}
}
sum[n] = max(dynamic_planning[i - 1][0], dynamic_planning[i - 1][1]);
n++;
if (n == i)
{
break;
}
}
int max = sum[0];
n = 0;
for (j = 0; j < i; j++)
{
if (sum[j]>max)
{
max = sum[j];
n = j;
}
}
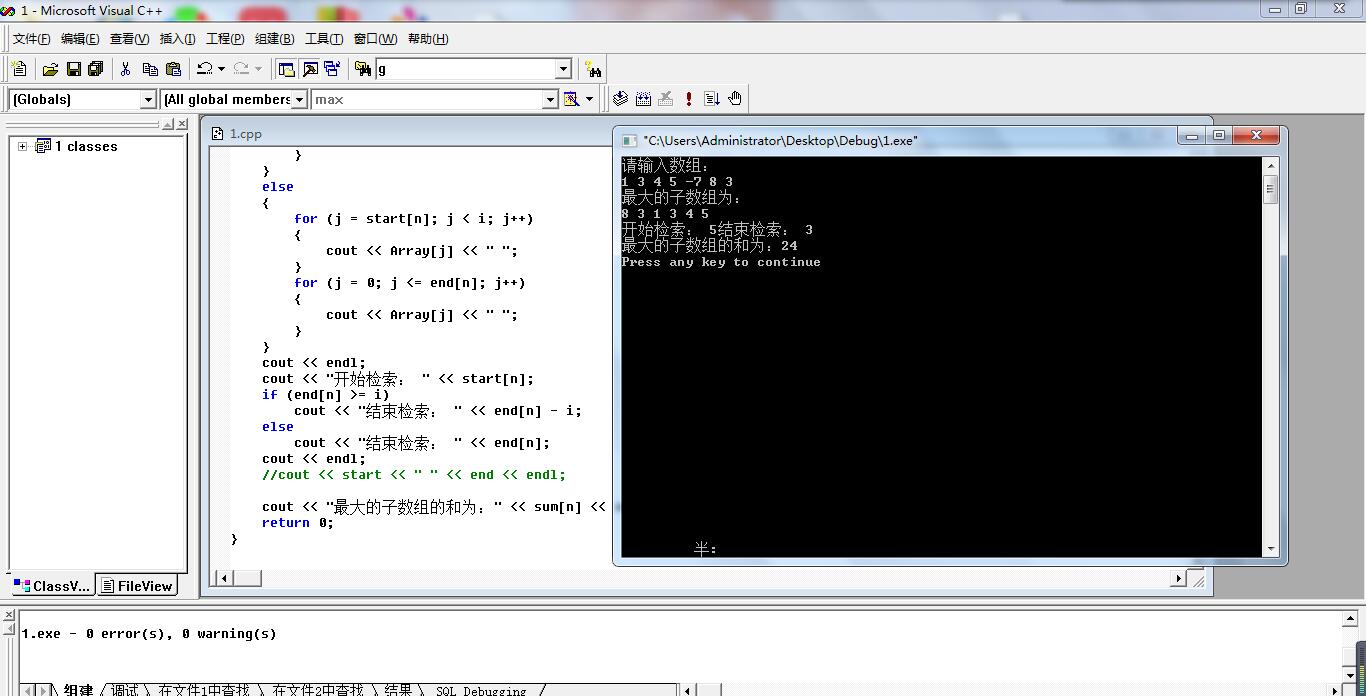
cout << "最大的子陣列為:" << endl;
if (start[n] <= end[n])
{
for (j = start[n]; j <= end[n]; j++)
{
cout << Array[j] << " ";
}
}
else
{
for (j = start[n]; j < i; j++)
{
cout << Array[j] << " ";
}
for (j = 0; j <= end[n]; j++)
{
cout << Array[j] << " ";
}
}
cout << endl;
cout << "開始檢索: " << start[n];
if (end[n] >= i)
cout << "結束檢索: " << end[n] - i;
else
cout << "結束檢索: " << end[n];
cout << endl;
//cout << start << " " << end << endl;
cout << "最大的子陣列的和為:" << sum[n] << endl;
return 0;
}
using namespace std;
int max(int a, int b)
{
if (a > b)
{
return a;
}
else
{
return b;
}
}
int main()
{
int Array[10000];
int i = 1,k;
int dynamic_planning[10000][2], j, sum[10000];
int start[10000] = {0};
int end[10000] = { 0 };
cout << "請輸入陣列:" << endl;
cin >> Array[0];
while (cin.get() != '\n')
{
cin >> Array[i++];
}
for (j = i; j < 2 * i; j++)
{
Array[j] = Array[j - i];
}
int n = 0;
while (true){
dynamic_planning[0][0] = 0;
dynamic_planning[0][1] = Array[n];
for (j = 1; j<i; j++)
{
dynamic_planning[j][0] = max(dynamic_planning[j - 1][0], dynamic_planning[j - 1][1]);
dynamic_planning[j][1] = max(Array[j+n], (dynamic_planning[j - 1][1] + Array[j+n]));
if (dynamic_planning[j - 1][1] < dynamic_planning[j][1] && dynamic_planning[j - 1][1]<0 && dynamic_planning[j][0] <= dynamic_planning[j][1])
{
start[n] = j+n;
}
if (dynamic_planning[j - 1][1] >= dynamic_planning[j][0])
{
end[n] = j-1+n;
}
if (dynamic_planning[j][1] >= dynamic_planning[j][0])
{
end[n] = j+n;
}
}
sum[n] = max(dynamic_planning[i - 1][0], dynamic_planning[i - 1][1]);
n++;
if (n == i)
{
break;
}
}
int max = sum[0];
n = 0;
for (j = 0; j < i; j++)
{
if (sum[j]>max)
{
max = sum[j];
n = j;
}
}
cout << "最大的子陣列為:" << endl;
if (start[n] <= end[n])
{
for (j = start[n]; j <= end[n]; j++)
{
cout << Array[j] << " ";
}
}
else
{
for (j = start[n]; j < i; j++)
{
cout << Array[j] << " ";
}
for (j = 0; j <= end[n]; j++)
{
cout << Array[j] << " ";
}
}
cout << endl;
cout << "開始檢索: " << start[n];
if (end[n] >= i)
cout << "結束檢索: " << end[n] - i;
else
cout << "結束檢索: " << end[n];
cout << endl;
//cout << start << " " << end << endl;
cout << "最大的子陣列的和為:" << sum[n] << endl;
return 0;
}


設計思路:我們根據只有前半部分的和為正數時,才有可能在子陣列求和的時候可能最大,演算法是當從頭開始,遍歷的元素求和為正數時,繼續向後遍歷,當求和為負數時,重新開始計算求和,子陣列的開始重置為下一個元素要求。這個作業不容易,是我們一點一點查書和查網上的程式碼改編的,要加強c基礎語句的應用。
