演算法之八大排序
演算法之八大排序
氣泡排序
1.排序思想
從無序序列頭部開始,進行兩兩比較,根據大小交換位置,直到最後將最大的資料元素交換帶無序佇列隊尾, 下一次繼續這個過程。
2.時間複雜度
最好情況: O(n) 給出的資料有序
最壞情況: O(n^2) 無序
3.空間複雜度
O(1)
4.穩定性
穩定
5.用畫圖的方式結合文字進行總結
6.程式碼實現與分析
public static void bubbleSort(int[] array) { boolean swap = false; //表示是否發生交換 for (int i = 0; i < array.length - 1; ++i) { //外層迴圈,次數 for (int j = 0; j < array.length - 1 - i; ++j) {//內層迴圈,每一次的比較 if (array[j] > array[j + 1]) { int tmp = array[j]; //將前面大數字和後面小數字進行交換 array[j] = array[j + 1]; array[j + 1] = tmp; swap = true; //如果交換 swap就換成true } } if (!swap) { break; } } }
選擇排序
1.排序的思想
在執行第i趟操作作時候,從第i條記錄後選擇一條最小的記錄和第i條進行比較交換
2.時間複雜度
O(n^2)
3.空間複雜度
O(1)
4.穩定性:
不穩定
5.用畫圖的方式結合文字進行總結
- 程式碼實現與分析
public static void selectSort(int[] array){ int tmp = 0; for (int i = 0; i<array.length;++i){//遍歷陣列 for (int j = i+1;j<array.length;++j){ //每次載遍歷i後面的 數字 if (array[i]>array[j]){//每次將i與j進行比較然後交換 tmp = array[i]; array[i] = array[j]; array[j] = tmp; } } } }
直接插入排序
1.排序的思想
每一次將一個待排序的元素,按其數字的大小插入到前面已經排好序的一組元素的合適位置上去,直到元
素全部插完為止。(分組排序)
2.時間複雜度
最優情況下: O(n) 給出的資料有序
最差情況下: O(n^2) 無序
3.空間複雜度
O(1)
4.穩定性
穩定
- 優化
希爾排序從某種意義上(分組)是對直接插入排序的優化
用畫圖的方式結合文字進行總結
7.程式碼實現與分析
public static void insertSort(int[] array){ int tmp = 0; int j = 0; for (int i = 1;i<array.length;++i) {//因為第一個數字不需要排序 所以i=1 tmp = array[i]; for ( j = i-1; j >= 0; --j) { //遍歷待排數字後面的數字 然後進行比較交換 if (array[j] > tmp) { //將大的數字往後挪 array[j+1] = array[j]; }else{ break; //找到比待排數字小的數字就跳出迴圈,前面已經有序了 } } array[j+1] = tmp; } }
Shell排序
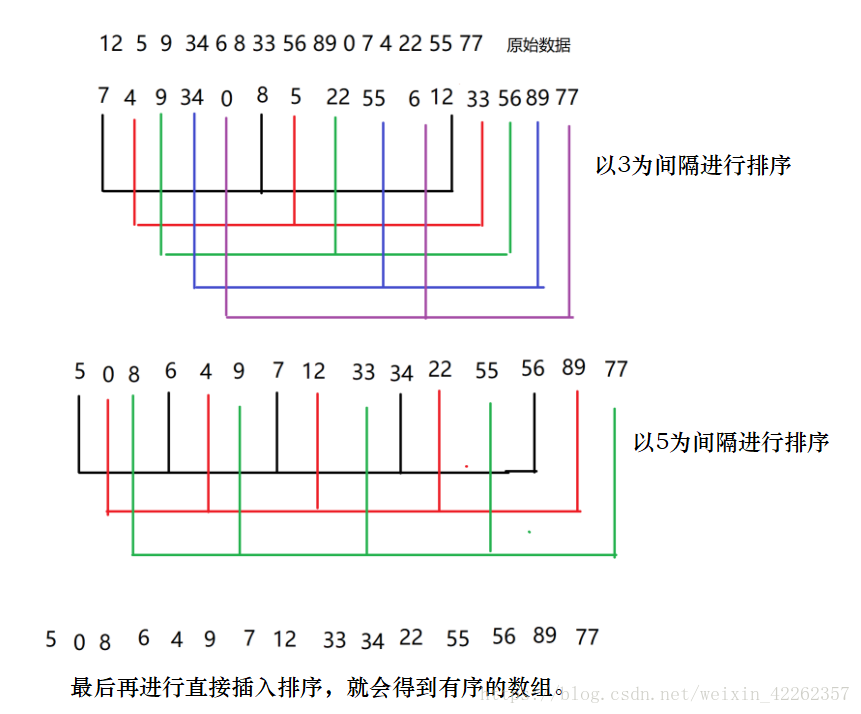
1.排序思想
待排序列有n個元素,先去一個小於n的整數h1作為第一個增量,把待排序列以間隔h1分成若干子序列,子序列內使用插入排序;然後取第二個增量h2,(<h1),重複上述的劃分和排序,直到索取的增量h1
= 1(h1 > h2 > ……>hi)。
2.時間複雜度
Shell排序是一種不穩定的排序演算法,文獻表明其時間複雜度受增量序列的影響明顯大於其他因素,最環的情況是O(n2),好的情況在O(n1.3),與增量序列選擇有關。
3.空間複雜度
O(1)
4.穩定性
不穩定
5.用畫圖的方式結合文字進行總結
6.程式碼實現與分析
public static void shell(int[] array,int gap){
for (int i = gap;i<array.length;++i){ //以gap為間隔 分成若干進行遍歷
int tmp = array[i];
int j = 0;
for (j = i-gap;j>=0;j -= gap){ //記錄後移,查詢插入的位置
if (array[j] >tmp){
array[j+gap] = array[j];
}else{
break;
}
}
array[j+gap] = tmp;
}
}
public static void shellSort(int[] array){
int[] drr = {5,3,1}; //建立一個數組,為排序只作為間隔的值
for (int i = 0;i<drr.length;++i){
shell(array,drr[i]);
}
}
快速排序
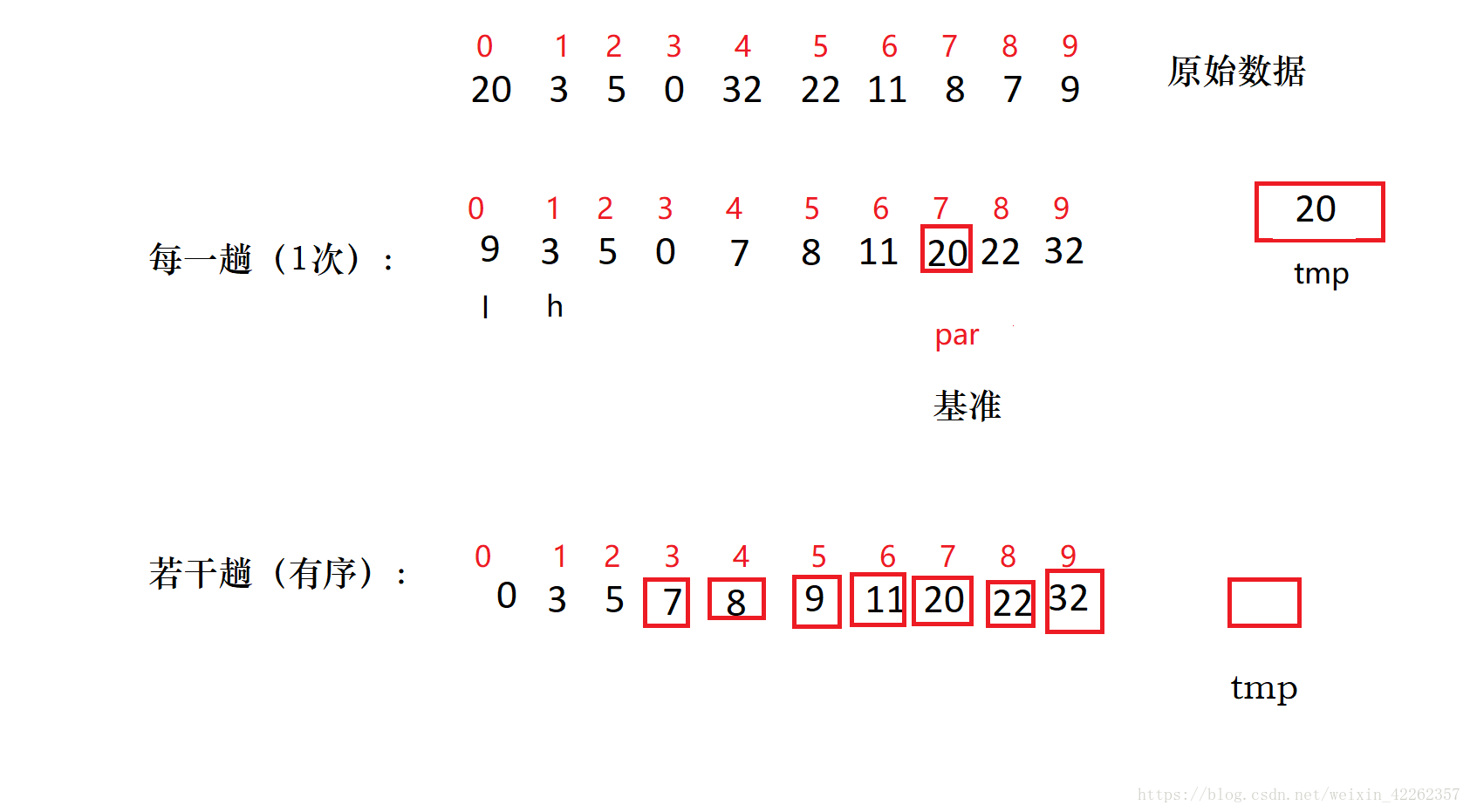
1.快速排序的思想
先從數列中取出一個數作為基準數;分割槽過程,將比這個數大的數全放到它的右邊,小於或等於它的數全放到它的左邊;再對左右區間重複第二步,直到各區間只有一個數。
2.時間複雜度
最好情況:O(nlog2n)
最快情況:O(n2)
3空間複雜度
O(log2n)
4.穩定性
不穩定
5.優化
第一種:當資料量少的時候有插入排序 ;第二種:聚焦相同的基準元素法
6.用畫圖的方式結合文字進行總結
7.程式碼實現與分析
import java.util.Arrays;
import java.util.Random;
/**
* Created with IntelliJ IDEA.
* Description:快排的三種排序方式以及兩種優化方式
* 排序方式:1.固定位置選取基準法 2.隨機選取基準法 3.三分取中法
* 優化方式:1、當資料量少的時候用插入排序 2.聚集相同基準元素法
* User: GAOBO
* Date: 2018-09-16
* Time: 17:27
*/
public class src2 {
public static int partion(int[] array,int low,int high) {
int tmp = array[low];
while (low < high) {
while(low < high && array[high] >= tmp) {
high--;
}
if(low >= high) {
break;//array[low] = tmp;
} else {
array[low] = array[high];
}
while(low < high && array[low] <= tmp) {
low++;
}
if(low >= high) {
break;
} else {
array[high] = array[low];
}
}
array[low] = tmp;//par
return low;
}
public static void swap(int[] array,int low,int high) {
int tmp = array[low];
array[low] = array[high];
array[high] = tmp;
}
// 排序方法:3.三分取中法
public static void medianOfThree(int[] array,int low,int high) {
int mid = (high+low)>>1;
//array[mid] <= array[low] <= array[high]
if(array[low] > array[high]) {//array[low] <= array[high]
swap(array,low,high);
}
if(array[low] < array[mid]) {//array[mid] <= array[low]
swap(array,low,mid);
}
if(array[mid] > array[high]) {//array[mid] <= array[high]
swap(array,mid,high);
}
}
//優化:1、當資料量少的時候用插入排序
public static void insertSort(int[] array,int low,int high) {
int tmp = 0;
for(int i = low+1;i < high;i++) {
tmp = array[i];
int j = 0;
for(j = i-1;j >= low;j--) {
if(tmp < array[j]) {
array[j+1] = array[j];
} else {
break;
}
}
array[j+1] = tmp;
}
}
//優化:2.聚集相同基準元素法
public static int[] focusParNum(int[] array,int low,int high,int par,
int left,int right) {
int[] brr = new int[2];
int parR = par+1;
int parL = par-1;
for(int i = par-1;i >= low;i--) {
if(array[i] == array[par]) {
if(i != parL) {
swap(array,i,parL);
parL--;
} else {
parL--;
}
}
}
left = parL;
for(int i = par+1;i <= high;i++) {
if(array[i] == array[par]) {
if(i != parR) {
swap(array,i,parR);
parR++;
} else {
parR++;
}
}
}
right = parR;
brr[0] = left;
brr[1] = right;
return brr;
}
public static void quick(int[] array,int low,int high) {
//優化方式1:資料量少的時候 用直接插入排序
/*if(high - low < 100) {
//直接插入排序
System.out.println("insert comeing");
insertSort(array,low,high);
}*/
/*
1、無限趨近於一個終止條件
2、迴圈呼叫自己本身
*/
/* //方式2、隨機選取基準法
Random random = new Random();
//low --- high 2 7 7-2 = 5 === [0,5)
//6 8 2===>[0,2)===0,1+6
int rand = random.nextInt((high-low)+1+low);
//low rand
swap(array,low,rand);
//方式3、三分取中法*/
medianOfThree(array,low,high);
int par = partion(array,low,high);//一次劃分函式,第一個par//O(n)
//優化方式2:聚集相同基準元素法
int left = par-1;
int right = par+1;
int[] brr = focusParNum(array,low,high,par,left,right);
left = brr[0];
right = brr[1];
//保證一個前提:必須有兩個資料以上
if(par > low+1) {//log2n
quick(array,low,left);
}
if(par < high-1) {
quick(array,right,high);
}
}
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
public static String getColumnLable(int n) {
String tmp = "";
// 按位找
int count = 1;
while (((int) (n / Math.pow(26, count-1)) > 0)) {
int w3 = ((int) (n % Math.pow(26, count)) / (int) Math.pow(26, count - 1));
char c = (char) (w3 + 64);
tmp = c + tmp;
count++;
}
return tmp;
}
堆排序
1.堆排序的基本思想
堆排序的原理就是這樣,先構造出來大根堆(假設從小到大排序),然後取出堆頂元素(也就是最大的元素),放到陣列的最後面,然後再將剩餘的元素構造大根堆,再取出堆頂元素放到陣列倒數第二個位置,依次類推,知道所有的元素都放到陣列中,排序就完成了
2.時間複雜度
O(nlog2n)
3.空間複雜度
O(1)
4.穩定性
不穩定
5.用畫圖的方式結合文字進行總結
6.程式碼實現與分析
public static void adjust(int[] array,int start,int end) {
int tmp = array[start];
for(int i = 2*start+1; i <= end;i = i*2+1) {
//1、是否有右孩子,如果有i表示的就是大的數字的下標
if((i < end-1) && array[i] < array[i+1]) {
i++;
}
if(array[i] > tmp) {
array[start] = array[i];
start = i;
}
if(array[i] <= tmp) {
break;
}
}
array[start] = tmp;
}
public static void heapSort(int[] array) {
//1、調整大根堆
for(int i = (array.length-1-1)/2;i >= 0;i--) {
adjust(array,i,array.length);
}
//1.交換 2.調整
for(int j = 0;j < array.length-1;j++) {
int tmp = array[0];
array[0] = array[array.length-1-j];
array[array.length-1-j] = tmp;
//-1:上面交換過後的節點不計算
adjust(array,0,array.length-1-j-1);
}
}
歸併排序
1.歸併排序的基本思想:
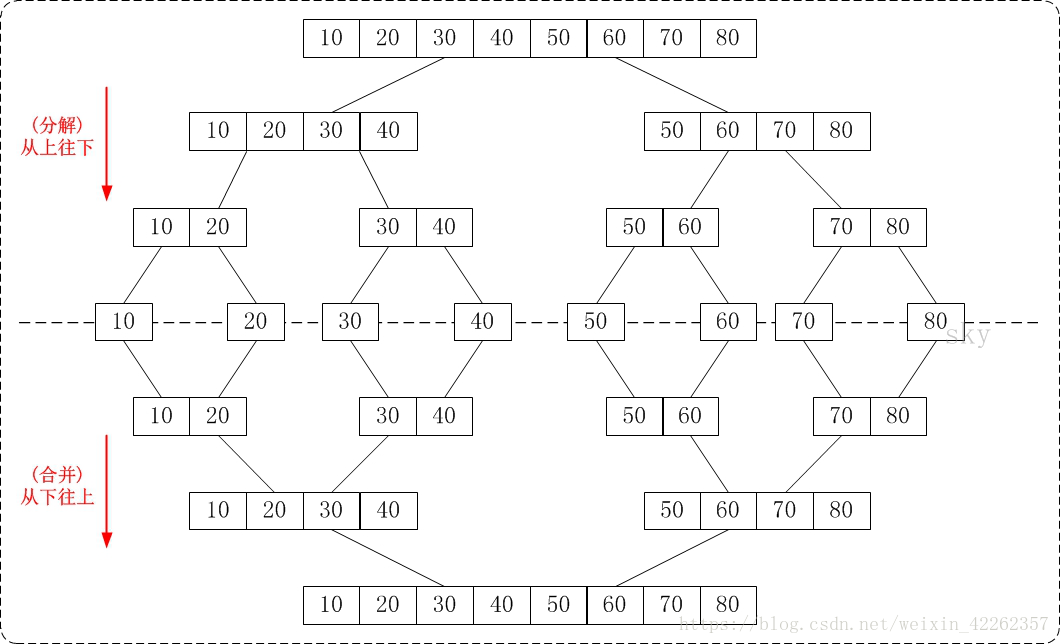
歸併排序就是利用歸併思想對數列進行排序。根據具體的實現,歸併排序包括"從上往下"和"從下往上"2種方式。
第一是從下往上的歸併排序:將待排序的數列分成若干個長度為1的子數列,然後將這些數列兩兩合併;得到若干個長度為2的有序數列,再將這些數列兩兩合併;得到若干個長度為4的有序數列,再將它們兩兩合併;直接合併成一個數列為止。這樣就得到了我們想要的排序結果。第二是從上往下的歸併排序:它與"從下往上"在排序上是反方向的。它基本包括3步:
① 分解 – 將當前區間一分為二,即求分裂點 mid = (low + high)/2; ② 求解 –
遞迴地對兩個子區間a[low…mid] 和 a[mid+1…high]進行歸併排序。遞迴的終結條件是子區間長度為1。 ③ 合併 –
將已排序的兩個子區間a[low…mid]和 a[mid+1…high]歸併為一個有序的區間a[low…high]。
2.時間複雜度
O(nolg2n)
3.空間複雜度
O(n)
4.穩定性
穩定
5.用畫圖的方式結合文字進行總結
6.程式碼實現與分析
public static void mergeSort(int[] array){
for (int i = 1;i<array.length;i *= 2){
merge(array,i);
}
}
private static void merge(int[] array, int gap) {
int[] tmp = new int[array.length];
int i = 0;//表示陣列tmp的下標
//確定s1,s2,e1,e2
int start1 = 0;
int end1 = start1 + gap-1;
int start2 = end1+1;
int end2 = start2 + gap-1 < array.length-1 ? start2 + gap-1 : array.length-1;
//判斷是否有兩個歸併段
while (start2 < array.length){
while (start1 <= end1 && start2 <= end2){
if (array[start1] < array[start2]){
tmp[i++] = array[start1++];
}else{
tmp[i++] = array[start2++];
}
}
//1.退出上面迴圈兩種條件
while (start2 <= end2) {
tmp[i++] = array[start2++];
}
//2.start2 > end2
while (start1 <= end1) {
tmp[i++] = array[start1++];
}
//重新對start1 end1 start2 end2 賦值
start1 = end2+1;
end1 = start1 + gap-1;
start2 = end1+1;
end2 = start2 + gap-1 < array.length-1 ? start2 + gap-1 : array.length-1;
}
while (start1 < array.length){
tmp[i++] = array[start1++];
}
System.arraycopy(tmp,0,array,0,array.length);
}
基數排序
1.基數排序基本思想:
基數排序是這樣一種排序演算法,我們可以從低位(個位)開始,根據個位數排序一次,然後根據十位數排序,再根據百位數進行排序……最終完成整個陣列的排序。
對於十進位制數字而言,每一位只會是 0~9 這十個數字,我們通常使用桶排序(計數排序)來完成每一位數的排序。桶排序是一種穩定的排序演算法,基數排序的正確性依賴一種穩定的排序演算法。
基數排序其實是分 LSD(從低位向高位排序) 和 MSD(從高位向低位排序) 兩種。
2.時間複雜度:
基數排序的時間複雜度為 O(n)。
基數排序使用桶排序對其每一位進行排序,即每一位的排序時間複雜度為 O(n),假設最大的數有 digit 位,則共需要進行 digit * O(n) 次排序。時間複雜度依舊為 O(n)。
3.畫圖示意: