分類：基於規則的分類技術

阿新 • • 發佈：2018-11-04

基於規則的分類是一種比較簡單的分類技術，下面從以下幾個方面對其進行介紹

1.任務

所有的分類技術的任務都是利用資料集訓練出分類器，然後為每條記錄貼上標籤，對其進行分類，基於規則的分類任務也是如此。

2.結構

基於規則的分類使用了一組 $"if...then..."$ 的規則來對記錄進行分類，其將這些規則組合起來，形成了如下所示結構

從上之下，當前規則去匹配記錄，若當前規則與記錄不匹配，則用下一條規則去匹配，直至找到能匹配的規則或者規則用完，結束分類過程。規則所處的位置可以用秩來表示，第一條規則秩最高，最後一條規則秩最低。

每一個分類規則可以表示為如下形式

$r_{i}:(c_{i})\rightarrow y_{i}$

$c_{i}$ 稱為規則前件( $rule\: antecedent$ )或前提( $precondition$ )，規則前件是屬性測試的集合

$c_{i}=(A_{1}\; op\; v_{1})\wedge (A_{2}\; op\; v_{2})\wedge...\wedge(A_{i}\; op\; v_{i})$

$(A_{i},v_{i})$ 為（屬性，值）對， $op$ 為比較運算子，取自集合 $\left \{ =,\not\equiv,<,>,\leqslant ,\geqslant \right \}$ ， $y_{i}$

為分類標籤，稱為規則後件。當規則 $r$ 的規則前件與記錄 $x$ 的屬性匹配時，則稱 $r$ 覆蓋 $x$ ；當 $r$ 覆蓋某條記錄時，則稱規則 $r$ 被觸發。

3.評分函式

基於規則的分類器的分類質量可以用覆蓋率(coverage)和準確率(accuracy)來度量，二者的定義分別為

覆蓋率：觸發了規則的記錄在資料集D中所佔的比例
準確率：在觸發了規則的記錄中，分類正確的記錄所佔比例

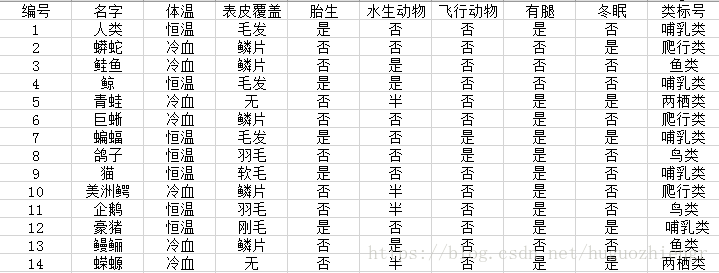
舉個例子對覆蓋率和準確率的定義進行說明，在脊椎動物的分類中，現有規則

（胎生=是）^（體溫=恆溫） $\rightarrow$ 哺乳類

資料集D為

在以上14條記錄中，記錄1、4、7、9、12觸發了規則，這5條記錄的分類全部正確，該分類器的覆蓋率及正確率分別為

$Coverage(r)=\frac{5}{14}=0.357$

$Accuracy(r)=\frac{5}{5}=1$

4.搜尋、優化方法

4.1規則集的性質

在基於規則的分類器中，規則必須滿足以下兩條重要性質

規則互斥：一條記錄不能觸發兩條及兩條以上規則
規則窮舉：資料集中每一條記錄都能被規則覆蓋

實現規則互斥，可以採用有序規則和無序規則兩種方案。在有序規則方案中，規則集中的規則按照優先順序降序排列，由覆蓋記錄的最高秩規則對記錄分類，這樣就避免多條規則間對記錄分類的衝突。有序的規則集也稱為決策表，第2節中介紹的分類器結構就是用的有序規則；在無序規則方案中，允許一條記錄觸發多條規則，規則被觸發時視為對其相應類的一次投票，然後計算不同類的票數（可以使用加權方式）來決定記錄的類所屬。

基於有序規則的分類器對規則排序非常敏感，但是對記錄分類時比較容易，不必把記錄與每一條規則的前件進行比較，而基於無序規則的分類器則正好相反。在應用中計算量是一個需要重要點考慮的問題，因此一般基於規則的分類器採用有序規則。

在有序規則中，規則的排序有兩種方案，一是基於規則的排序方案，二是基於類的排序方案。

4.2規則的排序

在基於規則的排序方案中，依據規則質量的某種度量（比如整體分類正確率等，具體的度量方式在不同的基於規則分類演算法中會有所不同）對規則排序，這種排序方式確保每一個測試記錄都由覆蓋它的“最好的”規則來分類，這種分類方式能使得分類器的某種效能（即選擇的規則質量的某種度量）達到最好，但是對於秩較低的規則，則不容易解釋，因為它必須不滿足秩高於它的規則中的至少一個（屬性，值）。

在基於類的排序方案中，屬於同一個類的規則放在一起，然後按照對“類”排序的方式對這些規則進行排序，同一個類中的規則相互間的順序並不重要。這種排序方式使得每一條規則解釋起來相對容易，但是可能存在質量較差的規則（即不能正確決定記錄的型別）由於其所屬類的秩較高，導致其秩也較高，造成誤分類。

大多數著名的基於規則的分類器（如C4.5規則和RIPPER演算法）都採用基於類的排序方案，因此下文中介紹的建立分類器的過程，都是基於類的排序方案。

4.3規則的提取演算法

建立分類器的過程就是建立一套規則集，提取分類規則的方法有兩類：(1)直接法，直接從資料集中提取分類規則 (2)間接法，從其他的分類模型（如決策樹和神經網路）中提取分類規則，本文只說明使用直接法提取規則的過程。

順序覆蓋法(sequential covering)演算法經常被用來直接從資料中提取規則，該演算法每次提取一個類的規則，完成一個類的規則提取後再進行下一個類的規則提取。哪個類優先提取規則需要依據一定的原則，例如依據類包含的記錄比例，比例高的類優先提取規則，或者依據類中記錄的誤分類率高低等，此處類規則提取順序對應著4.2節中提到的類排序問題。順序覆蓋法的大致過程為：選擇一個類 $c$ ，資料集中屬於類 $c$ 的記錄稱為正例，否則稱為反例，從資料集中學習出一條規則 $r$ ，如果規則 $r$ 覆蓋大多數正例、沒有或極少數反例，則認為規則 $r$ 可取，並新增到規則集 $R$ 中。當然，這裡規則 $r$ 覆蓋多少正例、反例才是可取的需要使用某種度量來決定，後面會介紹。該演算法步驟如下

令E為訓練記錄，E中(屬性，值)集合 $A=\left \{ (A_{1},v_{1}),(A_{2},v_{2}),...,(A_{k},v_{k}) \right \}$ ，類集合 $Y=\left \{ y_{1},y_{2},...,y_{k} \right \}$
令 $R=\left \{ \right \}$ 為初始規則列表，
for ，表示空
- while 終止條件不滿足
  - $r=\leftarrow LearnOneRule(E,A,y)$
  - $E=E-E_{r}$ ， $E_{r}$ 為 $r$ 覆蓋的記錄
  - $R\leftarrow R\vee r$ ，新增 $r$ 到 $R$ 末尾
- End While
End for

在該演算法中，while迴圈內的終止條件不唯一，在不同的分類器中可能會有區別，比如可以是所有整理均被覆蓋，也可以是剩餘正例比例小於某個閾值等。下面說明了順序覆蓋演算法提取一個類中規則 $r1$ 和 $r2$ 的過程，在該過程中，每次提取一個規則之後，就將改規則覆蓋的記錄（包括正例和反例）去掉，並且對於每個類中的每條規則，都是從完整的（屬性，值） $A$ 中提取。

在上述演算法中， $LearnOneRule(E,A,y)$ 函式的作用是依據訓練集 $E$ 、(屬性，值)集合 $A$ 以及當前選中的類 $y$ 生成一條分類規則，最先想到的方法可能是將 $A$ 中包含的(屬性，值)進行任意組合，形成規則，然後觀察不同規則覆蓋的正例和反例數，挑選符合要求的規則作為類 $y$ 的分類規則，但是這種方法的搜尋空間是指數級的（ $A$ 中包含(屬性，值)個數為 $p$ ，則其組合有 $p2^{p-1}$ 種），這在集合 $A$ 和訓練集 $E$ 比較龐大時計算難度是爆炸的，因此在實際應用中， $LearnOneRule(E,A,y)$ 函式中規則生成策略一般有兩種：從一般到特殊、從特殊到一般。

4.4規則生成策略

4.4.1 從一般到特殊

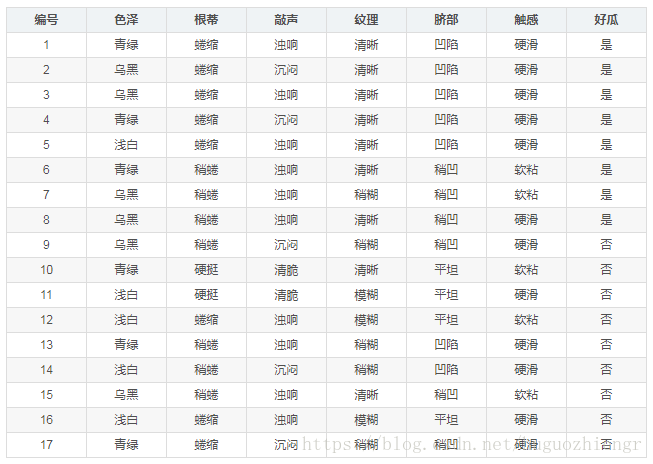
在該策略中，初始時規則 $r$ 前件為空，然後逐次的新增(屬性，值)對，滿足一定條件時停止新增(屬性，值)對，生成一條規則，這個過程要考慮兩個問題：(1)(屬性，值)新增（選擇）時的評估度量，決定(屬性，值)新增順序；(2)(屬性，值)新增的終止條件。(屬性，值)對的評估度量有多種，此處先以使用最簡單的一種度量——準確率（規則覆蓋的記錄中被正確分類的比例）來說明規則生成策略，具體的度量在後面介紹。(屬性，值)對新增的終止條件有三個：(1)新增(屬性，值)後度量效能不提升；(2)類中正例已被全部覆蓋，這實際上是條件(1)中的一種；(3)集合 $A$ 中(屬性，值)已新增完，需要注意的是這裡的終止條件與4.3節提到的演算法中while迴圈的終止條件的區別。下面舉例說明從一般到特殊的規則生成策略，現需要依據西瓜的特徵來判斷西瓜是好瓜還是壞瓜，訓練記錄如下

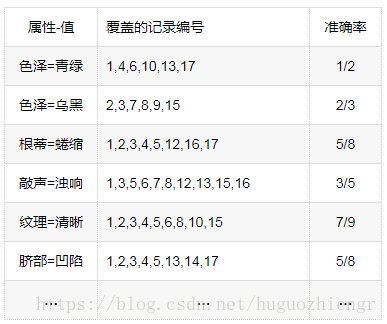
規則 $r$ 後件為（好瓜=是），前件從空開始，先新增第一個(屬性，值)，候選(屬性，值)、覆蓋的部分記錄編號及它的分類正確率分別如下

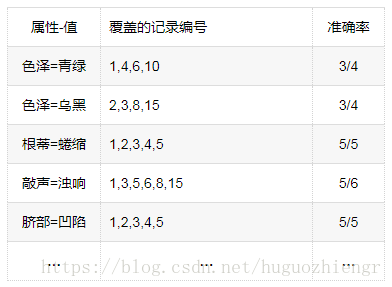
可以看到，(紋理=清晰)的正確率最高，因此首先在規則 $r$ 的前件中新增(紋理=清晰)，接著在(紋理=清晰)覆蓋的記錄中，繼續規則 $r$ 前件中(屬性，值)新增，候選的部分記錄編號及它的分類正確率分別如下

在(紋理=清晰)覆蓋的記錄中，(根蒂=蜷縮)與(臍部=凹陷)覆蓋記錄的正確率都達到了100%，可以任選一個(屬性，值)，這裡可以選擇(根蒂=蜷縮)（當出現這種情況時，可依據具體的任務和情況來考慮選擇哪個，比如先考慮準確率，若準確率相同可以考慮覆蓋率，若覆蓋率相同則可以考慮屬性出現的先後等），此時也達到了(屬性，值)新增的終止條件，故在類(好瓜=是)中， $LearnOneRule(E,A,y)$ 函式生成了第一條規則

{(紋理=清晰)^(根蒂=蜷縮)} $\rightarrow$ (好瓜=是)

接下來按照4.3節中的順序覆蓋演算法，可以繼續在類(好瓜=是)中生成規則。在順序覆蓋演算法中，每次生成一條規則後，需要去掉該規則覆蓋的記錄，然後用新的記錄集去生成下一條規則，而經常出現的情況是前後兩條規則覆蓋的記錄實際上是有重合的，從一般到特殊的規則生成策略中，每次只考慮一個最優的(屬性，值)，這顯得過於貪心，容易陷入區域性最優麻煩，為了緩解該問題，可以採用一種“集束搜尋(beam search)”的方式，具體做法為：每次選擇新增的(屬性，值)時，可以保留前 $k$ 個最優的(屬性，值)，而不是隻選擇最優的那個，然後對這 $k$ 個最優的(屬性，值)繼續進行下一輪的(屬性，值)新增。

4.4.2 從特殊到一般

這種策略是從比較特殊的規則開始，逐漸刪除(屬性，值)，滿足(屬性，值)刪除的終止條件：(1)刪除(屬性，值)後度量效能不提升；(2)類中正例已被全部覆蓋，這實際上是條件(1)中的一種；(3)(屬性，值)只剩下一個，規則生成的過程與4.4.1中類似。

從一般到特殊的策略更容易構建泛化效能比較好的分類器，且對噪聲的魯棒性更強，因此在一般的規則學習中通常採用該策略。從特殊到一般的策略適用於樣本比較少的情況，在一階規則學習這類假設空間比較複雜的任務上使用較多。

4.5規則評估

在4.4.1中提到了(屬性，值)新增（選擇）時的評估度量，用了“正確率”度量，然而把正確率作為一個度量標準有一個潛在的侷限性是沒有考慮規則的覆蓋率，例如考慮一個訓練集，它包含60個正例和100個反例，現有兩個候選規則

$r1:$ 覆蓋50個正例和5個反例

$r2:$ 覆蓋2個正例和0個反例

$r1$ 和 $r2$ 的正確率分別為90.9%、100%，然而 $r1$ 是較好的規則，儘管其準確率較低， $r2$ 的覆蓋率太低了，其高準確率可能是噪聲影響，具有潛在的欺騙性，以下幾種度量標準可以處理這個問題

4.5.1 似然比統計量

構造如下似然比統計量 $LRS$

$LRS=2 \sum_{i=1}^{k}f_{i}log_{2}(f_{i}/e_{i})$

$k$ : 規則覆蓋樣例中包含類的個數

$f_{i}$ : 屬於類 $i$ 的樣本的觀測頻率(類 $i$ 中包含的樣例個數)

$e_{i}$ : 在資料集中，規則做隨機猜測的期望頻率

在規則生成過程中，可以簡單認為 $k$ =2，只有正例和反例兩種， $e_{i}$ 也可以簡單的理解為記錄集中包含正例和反例的比例，較大的 $R$ 值表明做出正確預測數顯著大於隨機猜測的頻率。在上面的例子中

對規則 $r_{1}$

$f_{+}=50,f_{-}=5$ , $e_{+}=55\times 60/100=20.625$ , $e_{-}=55\times 100/160=34.375$

$LRS(r_{1})=2\times \left [ 50\times log_{2}(50/20.625)+5\times log_{2}(5/34.375) \right ]=99.99$

對規則 $r_{2}$

$f_{+}=2,f_{-}=0,e_{+}=2\times 60/100=0.75,e_{-}=2\times 100/160$

$LRS\left (r_{2} \right )=2 \times \left [ 2\times log_{2}(2/0.75)+0\times log_{2}(0/0.125) \right ]=5.66$

結果顯示規則 $r_{1}$ 比 $r_{2}$ 好

4.5.2 Laplace引數，m估計引數

Laplace引數考慮了規則的覆蓋率，其定義為

$Laplace=\frac{f_{+}+1}{n+k}$

$m=\frac{f_{+}+kp_{+}}{n+k}$

$n$ :規則覆蓋的樣例數

$f_{+}$ :規則覆蓋的正例數

$k$ :類的總數

$p_{+}$ :正類的先驗概率

先驗概率 $p_{+}=1/k$ 時，二者即相同。當覆蓋率很低或n=0時，兩個度量都接近於先驗概率，而當覆蓋率很高時，二者則接近於規則的準確率 $f_{+}/n$ 。在上面的例子中，

$Laplace(r_{1})=\frac{50+1}{55+2}=0.8947$

$Laplace(r_{2})=\frac{2+1}{2+2}=0.75$

結果顯示規則 $r_{1}$ 比 $r_{2}$ 好

4.5.2 FOIL資訊增益

假設規則 $r:A\rightarrow$ 覆蓋 $p_{0}$ 個正例和 $n_{0}$ 個反例，增加新的合取項 $B$ 後，擴充套件的規則 $r:B\rightarrow$ 覆蓋 $p_{1}$ 個正例和 $n_{1}$ 個反例，此時擴充套件規則後FOIL資訊增益定義為

$FOIL=p_{1}\times \left [ log_{2} \frac{p_{1}}{p_{1}+n_{1}}-log_{2}\frac{p_{0}}{p_{0}+n_{0}}\right ]$

該度量與 $p_{1}$ 和 $p_{1}/(p_{1}+n_{1})$ 成正比，所以它更傾向於選擇那些高支援度計數和高準確率的規則，上面的例子中，

$FOIL(r_{1})=50\times \left [ log_{2}\frac{50}{55}-log_{2}\frac{60}{160} \right ]=63.87$

$FOIL(r_{2})=2\times \left [ log_{2}\frac{2}{2}-log_{2}\frac{60}{160} \right ]=2.83$

結果顯示規則 $r_{1}$ 比 $r_{2}$ 好

4.6 剪枝

和決策樹分類一樣，剪枝的作用是緩解過擬合情況，提高基於規則的分類器的泛化能力，剪枝策略同樣分為預剪枝和後剪枝。

預剪枝發生在規則的生成過程中，選定4.5小節中介紹的某個度量，然後設定一個閾值，當新增(屬性，值)後度量的增加（或減少）的值不滿足閾值要求時，即停止(屬性，值)的新增。

後剪枝中最常用的策略是“減錯剪枝(Reduced Error Pruning，簡稱REP)”，其基本做法是：將樣例集分為訓練集和驗證集，從訓練集中學得規則集 $R$ 後進行多輪剪枝，在每一輪窮舉所有可能的剪枝操作，包括刪除某條規則、某條規則中的部分(屬性，值)等，然後用驗證集對剪枝後所有的候選規則集進行評估，保留最好的規則集進行下一輪剪枝，如此繼續，直到無法通過剪枝提高規則集在驗證集上的效能。REP剪枝方法通常比較有效，但是它針對整體規則集進行剪枝，複雜度太高了。

IREP(Incremental REP)方法的提出較大的降低了後剪枝的複雜度，其做法為：將樣例集分為訓練集和驗證集，在生成一條規則 $r$ 後，立即在驗證集上對該規則進行剪枝，得到規則 $r^'$ ，用 $r^'$ 替換 $r$ ，這樣的過程僅對單條規則進行剪枝，因此比REP更高效。

REP和IREP剪枝方法中用的度量不侷限於正確率，可以使用4.5節中合適的度量。

分類：基於規則的分類技術

1.任務

2.結構

3.評分函式