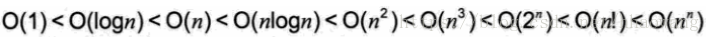資料結構-01-
1、 資料結構概念
1.1資料結構相關概念
1.1.1疑惑
1、我學完了C語言,可是現在感覺還是寫不出程式碼。
2、為什麼會有各種各樣的程式存在?
3、程式的本質是什麼?
- 程式是為了具體問題而存在的
- 程式需要圍繞問題的解決進行設計
- 同一個問題可以有多種解決方案
如何追求程式的“價效比”?
是否有可量化的方法判別程式的好壞?
1.1.2資料結構起源
- 計算機從解決數值計算問題到解決生活中的問題
- 現實生活中的問題涉及不同個體間的複雜聯絡
- 需要在計算機程式中描述生活中個體間的聯絡
- 資料結構主要研究非數值計算程式問題中的操作物件以及它們之間的關係
不是研究複雜的演算法
1.1.3資料結構中的基本概念
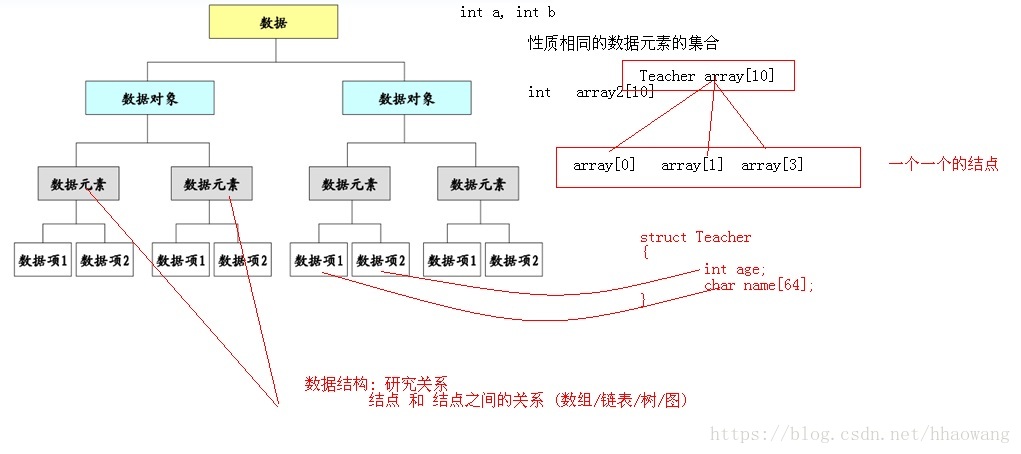
資料 – 程式的操作物件,用於描述客觀事物 (int a, int b,)
資料的特點:
- 可以輸入到計算機
- 可以被計算機程式處理
資料是一個抽象的概念,將其進行分類後得到程式設計語言中的型別。如:int,float,char等等
資料元素:組成資料的基本單位
資料項:一個數據元素由若干資料項組成
資料物件 – 性質相同的資料元素的集合 (比如:陣列,連結串列)
/宣告一個結構體型別 struct _MyTeacher //一種資料型別 { char name[32]; char tile[32]; int age; char addr[128]; }; int main21() { struct _MyTeacher t1; //資料元素 struct _MyTeacher tArray[30]; //資料物件 memset(&t1, 0, sizeof(t1)); strcpy(t1.name, "name"); //資料項 strcpy(t1.addr, "addr"); //資料項 strcpy(t1.tile, "addr"); //資料項 t1.age = 1; }
資料元素之間不是獨立的,存在特定的關係,這些關係即結構
資料結構指資料物件中資料元素之間的關係
如:陣列中各個元素之間存在固定的線性關係
編寫一個“好”的程式之前,必須分析待處理問題中各個物件的特性,以及物件之間的關係。
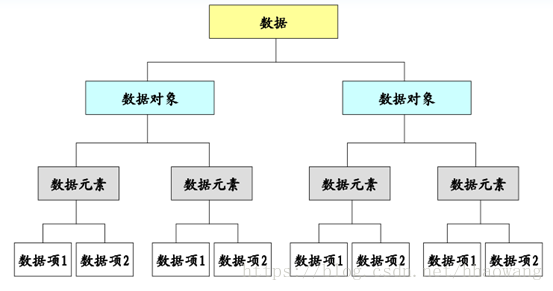
基本概念總結:
1.1.4資料的邏輯結構
指資料元素之間的邏輯關係。即從邏輯關係上描述資料,它與資料的儲存無關,是獨立於計算機的。邏輯結構可細分為4類:
1.1.5資料的物理結構
1.1.6資料的運算
1.2、演算法
1.2.1演算法概念
- 演算法是特定問題求解步驟的描述
- 在計算機中表現為指令的有限序列
- 演算法是獨立存在的一種解決問題的方法和思想。
對於演算法而言,語言並不重要,重要的是思想。
1.2.2演算法和資料結構區別
- 資料結構只是靜態的描述了資料元素之間的關係
- 高效的程式需要在資料結構的基礎上設計和選擇演算法
程式=資料結構+演算法
總結:
- 演算法是為了解決實際問題而設計的
- 資料結構是演算法需要處理的問題載體
- 資料結構與演算法相輔相成
1.2.3演算法特性
輸入
演算法具有0個或多個輸入
輸出
演算法至少有1個或多個輸出
有窮性
演算法在有限的步驟之後會自動結束而不會無限迴圈
確定性
演算法中的每一步都有確定的含義,不會出現二義性
可行性
演算法的每一步都是可行的
1.2.4演算法效率的度量
1、事後統計法
比較不同演算法對同一組輸入資料的執行處理時間
缺陷 :
- 為了獲得不同演算法的執行時間必須編寫相應程式
- 執行時間嚴重依賴硬體以及執行時的環境因素
- 演算法的測試資料的選取相當困難
- 事後統計法雖然直觀,但是實施困難且缺陷多
2、事前分析估算
依據統計的方法對演算法效率進行估算,影響演算法效率的主要因素有:
-
演算法採用的策略和方法
-
問題的輸入規模
-
編譯器所產生的程式碼
-
計算機執行速度
//演算法最終編譯成具體的計算機指令 //每一個指令,在具體的計算機上執行速度固定 //通過具體的n的步驟,就可以推匯出演算法的複雜度 long sum1(int n) { long ret = 0; int* array = (int*)malloc(n * sizeof(int)); int i = 0; for(i=0; i<n; i++) { array[i] = i + 1; } for(i=0; i<n; i++) { ret += array[i]; } free(array); return ret; } long sum2(int n) { long ret = 0; int i = 0; for(i=1; i<=n; i++) { ret += i; } return ret; } long sum3(int n) { long ret = 0; if( n > 0 ) { ret = (1 + n) * n / 2; } return ret; } int main() { printf("%d\n", sum1(100)); printf("%d\n", sum2(100)); printf("%d\n", sum3(100)); return 0; } int func(int a[], int len) { int i = 0; int j = 0; int s = 0; for(i=0; i<len; i++) n { for(j=0; j<len; j++) n { s += i*j; //n*n } } return s; } //n*n
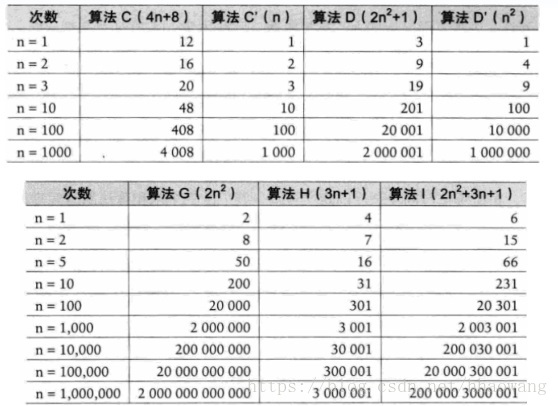
注意1:判斷一個演算法的效率時,往往只需要關注運算元量的最高次項,其它次要項和常數項可以忽略。
注意2:在沒有特殊說明時,我們所分析的演算法的時間複雜度都是指最壞時間複雜度。
2、大O表示法
- 演算法效率嚴重依賴於操作(Operation)數量
- 在判斷時首先關注運算元量的最高次項
- 運算元量的估算可以作為時間複雜度的估算
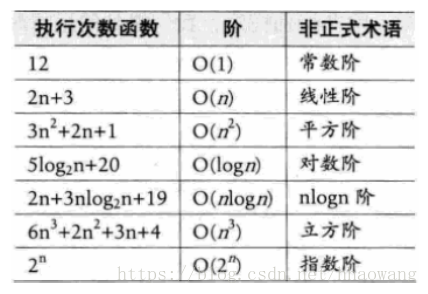
O(5) = O(1)
O(2n + 1) = O(2n) = O(n)
O(n2+ n + 1) = O(n2)
O(3n3+1) = O(3n3) = O(n3)
常見時間複雜度
關係
3、演算法的空間複雜度
演算法的空間複雜度通過計算演算法的儲存空間實現
S(n) = O(f(n))
其中,n為問題規模,f(n))為在問題規模為n時所佔用儲存空間的函式
大O表示法同樣適用於演算法的空間複雜度
當演算法執行時所需要的空間是常數時,空間複雜度為O(1)
空間與時間的策略
多數情況下,演算法執行時所用的時間更令人關注
如果有必要,可以通過增加空間複雜度來降低時間複雜度
同理,也可以通過增加時間複雜度來降低空間複雜度
練習1:分析sum1 sum2 sum3函式的空間複雜度
O(4n+12) O(8)=O(1) O(4)=O(1)
總結:實現演算法時,需要分析具體問題,對執行時間和空間的要求。
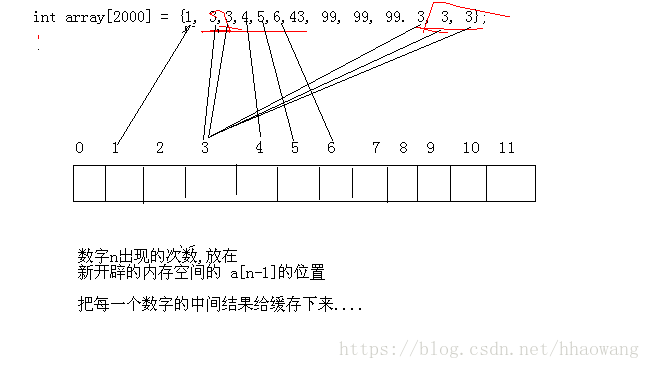
練習2:時間換空間
/*
問題:
在一個由自然數1-1000中某些數字所組成的陣列中,每個數字可能出現零次或者多次。
設計一個演算法,找出出現次數最多的數字。
*/
方法1:
排序,然後找出出現次數最多的數字
方法2:
void search(int a[], int len)
{
int sp[1000] = {0};
int i = 0;
int max = 0;
for(i=0; i<len; i++)
{
int index = a[i] - 1;
sp[index]++;
}
for(i=0; i<1000; i++)
{
if( max < sp[i] )
{
max = sp[i];
}
}
for(i=0; i<1000; i++)
{
if( max == sp[i] )
{
printf("%d\n", i+1);
}
}
}
int main()
{
int array[] = {1, 1, 3, 4, 5, 6, 6, 6, 2, 3};
search(array, sizeof(array)/sizeof(*array));
return 0;
}
把每個數字出現的次數的中間結果,快取下來;在快取的結果中求最大值。
另外:
MOOC《資料結構》課程內容總結見連結: