1.圖的定義：圖是一種網狀資料結構，形式化定義如下：圖Graph = (V, R)，V = {x | x ∈ DataObject}，R = {VR}，VR = {<x, y> | P(x, y) ∧ (x, y ∈ V)}。集合DataObject中的所有元素具有相同的特性。V中的資料元素通常為頂點(vertex)，VR是兩個頂點之間關係的集合，P(x, y)表示x和y之間有特定的關係屬性P。

（1）若<x, y> ∈ VR，則<x, y>表示從頂點x到頂點y的一條弧(arc)，並稱x為弧尾(tail)或起始點，稱y為弧頭(head)或終端點，此時圖中的邊是有方向的，稱這樣的圖為有向圖。

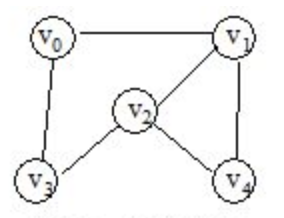
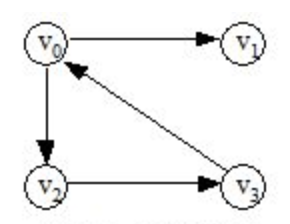
（2）若<x, y> ∈ VR，且有<y, x> ∈ VR，即VR是對稱關係，這時以無序對(x, y)來代替兩個有序對，表示x和y之間的一條邊(edge)，此時的圖稱為無向圖。如下圖，左圖為無向圖，右圖為有向圖：

ADT Graph

{

　　資料物件V：V是具有相同特性的資料元素的集合，稱為頂點集。

　　資料關係R：R = {VR}，VR = {<x, y> | P(x, y) ∧ (x, y ∈ V)}

　　基本操作P：

　　①CreateGraph(&G, V, VR)

　　   初始條件：V是圖的頂點集，VR是圖中弧的集合。

　　   操作結果：按V和VR的定義構造圖G。

　　②DestroyGraph(&G)

　　   初始條件：圖G存在。

　　   操作結果：銷燬圖G。

　　③LocateVex(G, u)

　　   初始條件：圖G存在，u和G中頂點有相同特徵。

　　   操作結果：若G中存在頂點u，則返回該頂點在圖中位置；否則返回其它資訊。

　　④GetVex(G, v)

　　   初始條件：圖G存在，v是G中某個頂點。

　　   操作結果：返回v的值。

　　⑤PutVex(&G, v, value)

　　   初始條件：圖G存在，v是G中某個頂點。

　　   操作結果：對v賦值value。

　　⑥InsertVex(&G, v)

　　   初始條件：圖G存在，v和圖中頂點有相同特徵。

　　   操作結果：在圖G中新增新頂點v。

　　⑦DeleteVex(&G, v)

　　   初始條件：圖G存在，v是G中某個頂點。

　　   操作結果：刪除G中頂點v及其相關的弧。

　　⑧InsertAcr(&G, v, w)

　　   初始條件：圖G存在，v和w是G中兩個頂點。

　　   操作結果：在G中增添弧<v, w>，若G是無向的，則還增添對稱弧<w, v>。

　　⑨DeleteArc(&G, v, w)

　　   初始條件：圖G存在，v和w是G中兩個頂點。

　　   操縱結果：在G中刪除弧<v, w>，若G是無向的，則還刪除對稱弧<w, v>。

　　⑩DFSTraverse(G, visit())

　　   初始條件：圖G存在，v是G中某個頂點，visit是頂點的應用函式。

　　   操作結果：深度優先遍歷圖個G，並對每個頂點呼叫函式visit一次。一旦visit失敗，則操作失敗。

　　⑪BFSTraverse(G, visit())

　　   初始條件：圖G存在，visit是頂點的應用函式。

　　   操作結果：廣度優先遍歷圖G，並對每個頂點呼叫函式visit一次，一旦visit失敗，則操作失敗。

}

2.完全圖：設n表示圖中頂點個數，用e表示圖中邊或弧的數目，且不考慮圖中每個頂點到其自身的邊或弧。

（1）無向完全圖：對於無向圖而言，其邊數e的取值範圍是0~n(n-1)/2。稱有n(n-1)/2條邊（即圖中每個頂點和其餘n-1個頂點都有邊相連）的無向圖為無向完全圖。

（2）有向完全圖：對於有向圖而言，其邊數e的取值範圍是0~n(n-1)。稱有n(n-1)條弧（即圖中每個頂點和其餘n-1個頂點都有弧相連）的有向圖為有向完全圖。

3.稀疏圖和稠密圖：對於有很少條邊的圖（e < nlogn）稱為稀疏圖，反之稱為稠密圖。

4.子圖：設圖G = (V, {VR})和圖G' = (V', {VR'})，且V' ⊆V，VR' ⊆ VR，則稱G'為G的子圖。

5.鄰接點：對於無向圖G = (V, {E})，如果邊(v, v') ∈ E，則稱頂點v，v'互為鄰接點，即v，v'相鄰接。邊(v, v')依附於頂點v和v'，或者說邊(v, v')與頂點v和v'相關聯。對於有向圖G = (V, {A})，如果弧<v, v'> ∈ A，則稱頂點v鄰接到頂點v'，頂點v'鄰接自頂點v，或者說弧<v, v'>與頂點v和v'相關聯。

6.度、入度和出度：對於無向圖而言，頂點v的度是指和v相關聯的邊的數目，記作(v)。在有向圖中，頂點v的度有出度和入度兩部分，其中以頂點v為弧頭的弧的數目稱為該頂點的入度，記作ID(v)，以頂點v為弧尾的弧的數目稱為該頂點的出度，記作OD(v)，則頂點v的度為TD(v) = ID(v) + OD(v)。

7.權與網：在一個圖中，每條邊上可以標上具有某種含義的數值，此數值稱為該邊的權，通常權為非負實數，可以表示從一個頂點到另一個頂點的距離或耗費等資訊。邊上帶有權的圖稱為帶權圖，也常稱作網。

8.路徑與迴路：無向圖G = (V, {E})中從頂點v到v'的路徑是一個頂點序列(v = v_i0, v_i1, v_i2, ... ,v_in = v')，其中（v_ij-1，v_ij） ∈ E，1 ≤ j ≤ n。如果圖G是有向圖，則路徑也是有向的，頂點序列應滿足<v_ij-1，v_ij> ∈ E，1 ≤ j ≤ n。路徑的長度是指路徑上經過的弧或邊的數目。在一個路徑中，若其第一個頂點和最後一個頂點是相同的，即v = v'，則稱該路徑為迴路或環。若表示路徑的頂點序列中的頂點各不相同，則稱這樣的路徑為簡單路徑。除了第一個和最後一個頂點外，其餘各頂點均不重複出現的迴路為簡單迴路。

9.連通圖：在無向圖G = (V, {E})中，若從v_i到v_j有路徑相通，則稱頂點v_i與v_j是連通的。如果對於圖中的任意兩個頂點v_i、v_j ∈ V，v_i，v_j都是連通的，則稱該無向圖G為連通圖。在有向圖G = (V, {A})中，若對於每對頂點v_i，v_j ∈ V且v_i ≠ v_j，從v_i到v_j和v_j到v_i都有路徑，則稱該有向圖為強連通圖。

10.連通分量：無向圖中的極大連通子圖稱為該無向圖的連通分量。任何連通圖的連通分量只有一個，即其自身。非連通的無向圖有多個連通分量。有向圖的極大強連通子圖稱為G的強連通分量。強連通圖只有一個強連通分量，即其自身。非強連通的有向圖有多個強連通分量。

11.生成樹：一個連通圖的生成樹是一個極小連通子圖，它含有圖中全部頂點，但是隻有足以構成一棵樹的n-1條邊。如果在一棵生成樹上新增一條邊，必定構成一個環。如果一個圖有n個頂點和小於n-1條邊，則是非連通圖，如果多於n-1條邊則一定有環。