一、前言

從今天起，就給大家分享一些樹的程式碼啦，不僅僅是二叉樹，我們要弄明白，普通的樹用資料結構怎麼儲存，它有哪些操作，它可以實現哪些功能？

可能大家要問了，二叉樹不是還沒有寫完嗎，線索二叉樹呢？二叉排序樹呢？平衡二叉樹呢？大家不要急，我們通過二叉樹來入門樹的演算法及程式碼實現，然後學習樹的基本操作，當大家對樹的瞭解比較深入，操作比較熟練的時候，我們再學深入的東西。

線索二叉樹可以使用建立的空指標，來加速前驅和後繼的訪問速度；

二叉排序樹是按照一定規律排序的資料儲存在樹中，例如從小到大的資料按照中序建立二叉樹即可得到二叉排序樹，二叉排序樹與後面的排序查詢演算法聯絡也比較廣泛；

平衡二叉樹是為了防止樹的高度增長過快，降低二叉排序樹的效能而設計的一種結構，要保證的是任意結點的左右子樹高度差的絕對值不超過1。

樹要比二叉樹難，二叉樹作為樹的特例，每個結點只有兩個子樹（存在或空），但是一棵普通的樹孩子數量不一定，所以在構圖過程中，沒有左右孩子之說，所以就涉及到二叉樹與最多有兩個叉的樹的區別。

如下圖中，如果當成一棵普通的樹來看，編號為1的結點有一個孩子結點，畫在右側，但是這個孩子是編號1的第一個孩子結點，而不是右孩子結點。如果看作一個二叉樹，那就是編號為1的右孩子結點。這塊大家一定要注意。

首先要給大家說一下樹轉換為二叉樹，轉化規律如下：

結點左指標指向第一個孩子結點，右指標指向它在樹中的相鄰兄弟結點

typedef struct CSNode {
	int data;
	struct CSNode *firstChild, *nextSibling;
}CSNode, *CSTree;

二、題目

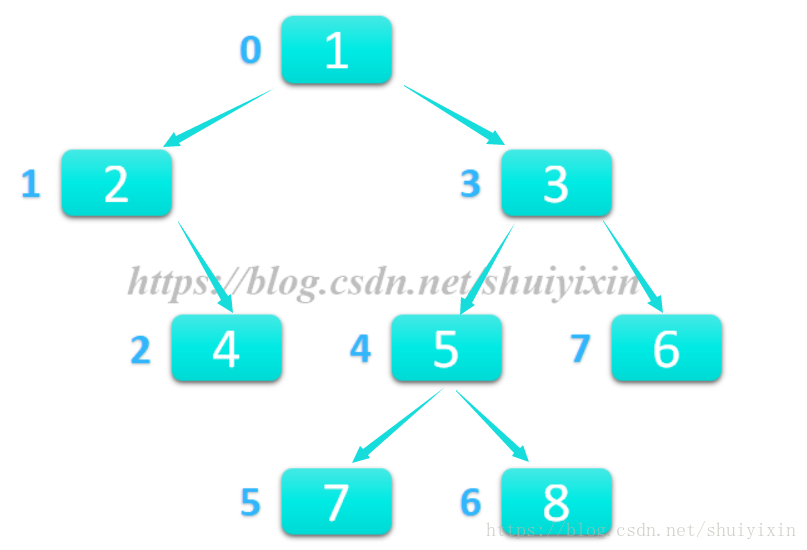
利用遞迴演算法及孩子兄弟表示法存入下圖的樹，求出每個結點的編號，資料及所有的孩子結點。其中圓角矩形內為結點資料，旁邊數字為結點編號，編號為0的結點為根節點，箭頭指向的結點為箭尾的孩子結點。

 三、程式碼

#define MAXQUEUESIZE 10

#include<iostream>
#include<malloc.h>

using namespace std;

typedef struct CSNode {
	int data;
	int number;
	struct CSNode *firstChild, *nextSibling, *parent;
}CSNode, *CSTree;

int number = 0;
int yon = 0;
int yesOrNo[] = { 1,1,0,0,1,1,1,0,1,0,0,1,0,0,0,0 };
int numData[] = { 1,2,4,3,5,7,8,6 };

CSTree treeParent = NULL;

int OperationTree(CSTree &T) {
	T = (CSTree)malloc(sizeof(CSNode));
	if (!T)
	{
		cout << "空間分配失敗(Allocate space failure.)" << endl;
		exit(OVERFLOW);
	}
	T->data = numData[number];
	T->number = number;
	number++;
	T->firstChild = NULL;
	T->nextSibling = NULL;
	T->parent = treeParent;	
	return 1;
}

int RecursionEstablishTree(CSTree &T) {
	OperationTree(T);
	treeParent = T;
	if (yesOrNo[yon++])
		RecursionEstablishTree(T->firstChild);
	treeParent = T;
	if (yesOrNo[yon++])
		RecursionEstablishTree(T->nextSibling);
	return 1;
}

void VisitCSTree(CSTree T) {
	cout << "The number of present node is ：" << T->number << ",";
	cout << "and the data is ：" << T->data << ".";
	if (T->firstChild) {
		cout << "This node has child and the number is :" << T->firstChild->number;
		CSTree p = T->firstChild;
		while (p->nextSibling) {
			cout << " , " << p->nextSibling->number;
			p = p->nextSibling;
		}
		
	}
	cout << endl;
}

//Visit tree use the preorder technique. 
void PreOrderVisitTree(CSTree T) {
	if (T)
	{
		VisitCSTree(T);
		PreOrderVisitTree(T->firstChild);
		PreOrderVisitTree(T->nextSibling);
	}
}

int TreeHeight(CSTree T) {
	int hc, hs;
	if (T == NULL)
		return 0;
	else
	{
		hc = TreeHeight(T->firstChild);
		hs = TreeHeight(T->nextSibling);
		if (hc + 1 > hs)
			return (hc + 1);
		else
			return hs;
	}
}

void main() {
	CSTree T;
	RecursionEstablishTree(T);
	PreOrderVisitTree(T);
	cout << "The hight of tree is :" << TreeHeight(T) << endl;
}

四、實現效果