SVM 覆盤總結
阿新 • • 發佈:2018-11-05
1. 硬間隔最大化:
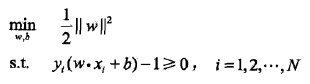
怎麼得到的?自己推導,可參考下圖推:
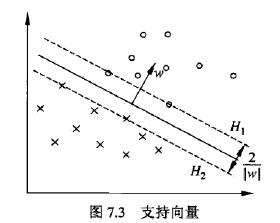
上述問題如何求解?
引入Lagrange function:
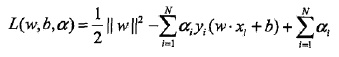
一系列推導之後,自己推導:

原始問題:
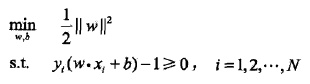
對偶優化問題:
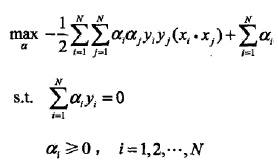
對偶問題求最最優:
怎麼求的SMO演算法如何實現,先等著?
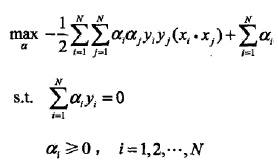
對α的解為:
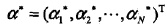
根據KKT條件,求得 和 :
KKT條件:
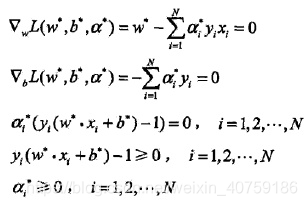
關注互補對偶條件如何得到的?
根據KKT條件,求得
和
:
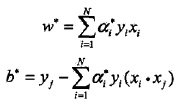
如何推導,自己推(選擇一個
> 0)
2. 軟間隔最大化
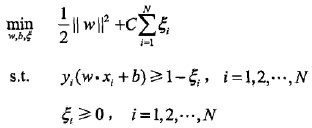
轉化為對偶問題:
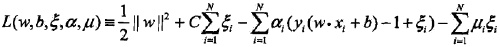
推導之後:
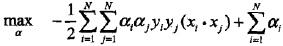
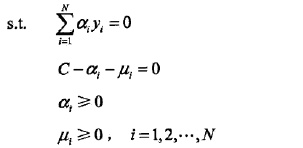
進一步轉化:
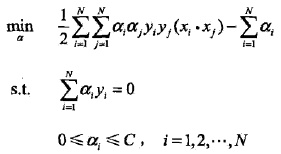
看到沒?硬的和軟的對偶函式之間區別,只在於
的區域,但是轉換為原目標最優還需要滿足KKT條件。
對α的解為:
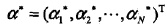
根據KKT條件,求得 和 :
KKT條件:
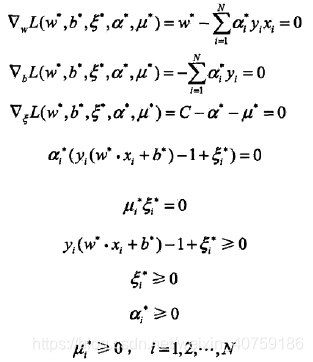
比較好求?
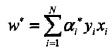
如何求
?
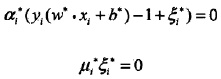
找一個0<
<C,則
= 0:
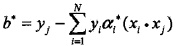
由於:
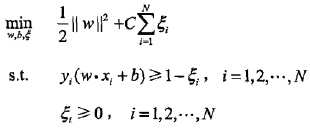
對b的解並不唯一,所以實際計算時可以取在所有符合條件的樣本點上的平均值。
這句話的理解:
是鬆弛因子,允許有些點在margin之內,0=<
,
=0,即
=C。
=C是有loss的。
需要分割儘量開,同時允許有一些異常點,異常點發生在
=C的點,0<
<C的點都是支援向量,因為有
=C的點存在,導致b有多個解,所以b要取所有b的均值,
=0的點沒有用。
3. Hinge Loss
軟間隔
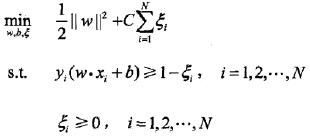
Hinge Loss
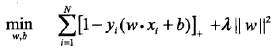
Hinge Loss就相當於鬆弛因子
對於間距大於一定程度的點,就沒有loss,就不用鬆弛。
正則化的作用相當於把分類的距離拉大。
4. 核函式
沒啥東西,目標函式暴走,目標函式只需要比較物件的距離,而不是其本身,利用目標函式的這個弱點使用了kernel trick。
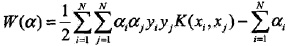
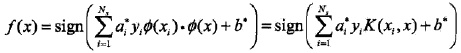
5. SMO演算法
SMO演算法要解如下凸二次規劃的對偶問題:
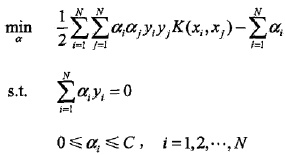
我們的解要滿足的KKT條件的對偶互補條件為:
根據這個KKT條件的對偶互補條件,我們有:
由於
,我們令
