既然上面提到了二叉樹的儲存結構，那麼我們進一步詳細介紹二叉樹的儲存結構

 

先複習一下 邏輯結構 與 物理結構：

邏輯結構講究的是資料之間的邏輯關係，分為：集合結構、線性結構、樹形結構、圖形結構

物理結構講究的是資料的儲存結構，分為：順序儲存結構、鏈式儲存結構

 

二叉樹的儲存結構——順序儲存 或者 鏈式儲存

 

以下針對如下這棵樹講解它的各種儲存方式

           

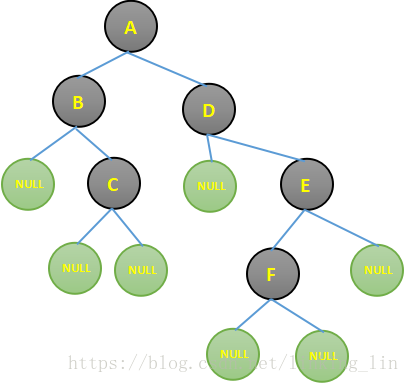
順序儲存

程式碼定義：

// The sequential storage of binary trees

#define MAX_TREE_SIZE 100

#define TElemType char

typedef TElemType SqBiTree[MAX_TREE_SIZE];

SqBiTree bt;

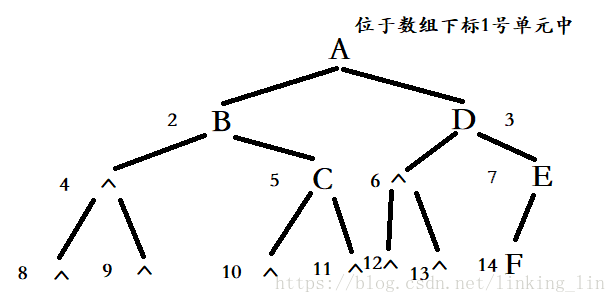
說明：

把樹中的結點 從上至下按層，每一層按照從左至右的方式存放在一個一維陣列中。

陣列的第一個下標為0的元素不使用，從下標為1的元素開始存放樹中的結點，

所以 樹的根結點 永遠放在下標為1的元素中。

注意：

因為這種方式既存放有值的結點，有存放空節點，

So這種儲存方式適合 結點總數少 或者 每層結點數儘量最多的情況，因為不浪費空間。

如果一棵二叉樹是單支樹（從根開始，只要一個結點有孩子，那麼只有一個左/右孩子），

那麼這種儲存方式很浪費空間。

這種儲存方式一般用於完全二叉樹和滿二叉樹。

鏈式儲存

4種：

1. 二叉連結串列

2. 三叉連結串列

3. 線索連結串列

4. 雙親陣列

 

——二叉連結串列（最常用）

程式碼定義：

// Binary list

#define ElemType char

typedef struct BiTNode{

    ElemType data;

    struct BiTNode *lchild,*rchild;

}*BiTree;

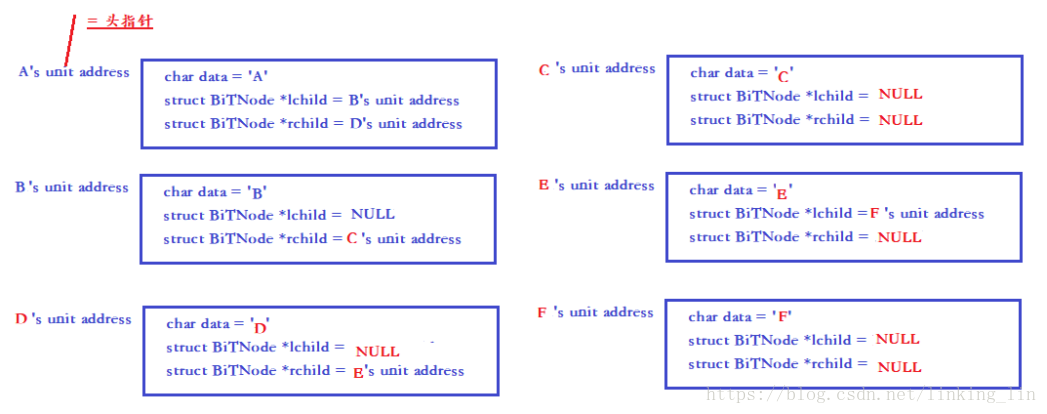
說明：

每個結點用一個結構體定義，結構體中的

data存放結點的數值；

lchild/rchild存放左/右孩子的地址；

注意：

左右孩子不是結構體 而是 指標，這樣做的好處是：

1. 同樣通過*符號訪問孩子結點的成員

2. 結構體型別變數佔的空間比指標大，結構體一般定義多個型別的成員，而指標就是一個地址變數，

可以通過程式的運算子sizeof檢視這兩種變數的記憶體佔用位元組大小

 

——三叉連結串列

程式碼定義：

// Trifurcate linked list

#define ElemType char

typedef struct TriTNode{

    Elemtype data;

    struct TriTNode *lchild,*rchild;

    struct TriTNode *parent;

}TriTNode, *TriTree;

說明：

在二叉連結串列的基礎上，增設一個指標，指向父結點的地址

——雙親陣列

程式碼定義：

#define MAX_TREE_SIZE 100

#define ElemType char

#define LRTagType int

#define lchild 0

#define rchild 1

 

typedef struct BPTNode{

    ElemType data;      //結點值域

    int parent;          //父結點在陣列中的下標

    LRTagType LRTag;    //標誌域:用於標記這個結點是父結點的左孩子還是右孩子

                      //       可以令其為0——左孩子，1——右孩子

}BPTNode;

 

typedef struct BPTree{

    BPTNode nodes[MAX_TREE_SIZE];// 雙親陣列

    int n;                       // n:樹中的結點個數

    int r;                       // r:樹根在陣列中的下標

}BPTree;

 

說明：

如果一個雙親陣列的內容如下

    

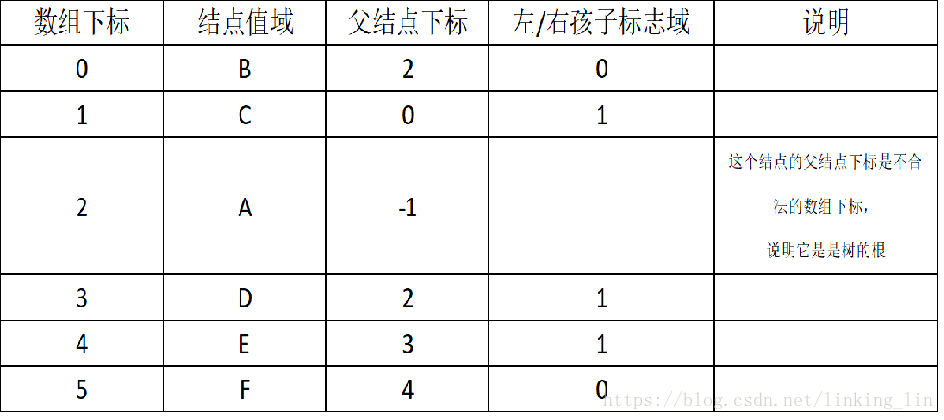
——線索連結串列（下次再說吧）