資料結構之-平衡二叉樹(AVL)
背景
不同結構的二叉查詢樹,查詢效率有很大的不同。如何解決這個問題呢?關鍵在於如何最大限度的減小樹的深度。正是基於這個想法,平衡二叉樹出現了。
前言
平衡二叉搜尋樹(英語:Balanced Binary Tree)是一種結構平衡的二叉搜尋樹。 它能在O(log n)時間內完成插入、查詢和刪除操作。它除了具備二叉查詢樹的基本特徵之外,還具有一個非常重要的特點:它的左子樹和右子樹都是平衡二叉樹,且左子樹和右子樹的深度之差的絕對值(平衡因子)不超過1。 也就是說平衡二叉樹每個節點的平衡因子只可能是-1、0和1(左子樹高度減去右子樹高度),最早被髮明的平衡二叉搜尋樹為AVL樹。
常見的平衡二叉搜尋樹有:
- AVL樹
- 紅黑樹
- Treap
- 節點大小平衡樹
如何使二叉查詢樹在新增資料的同時保持平衡呢?基本思想就是:當在二叉排序樹中插入一個節點時,首先檢查是否因插入而破壞了平衡,若 破壞,則找出其中的最小不平衡二叉樹,在保持二叉排序樹特性的情況下,調整最小不平衡子樹中節點之間的關係,以達 到新的平衡。所謂最小不平衡子樹指離插入節點最近且以平衡因子的絕對值大於1的節點作為根的子樹。
操作
1、查詢操作
平衡二叉樹的查詢基本與二叉查詢樹相同。
2、插入操作
在平衡二叉樹中插入結點與二叉查詢樹最大的不同在於要隨時保證插入後整棵二叉樹是平衡的。那麼調
失衡情況分析
在平衡二叉樹中,當我們插入新的元素時,為了保證二叉搜尋樹的特性,很容易導致某些結點失衡,即該結點的平衡因子大於1。
旋轉的目的就是減少高度,通過降低整棵樹的高度來平衡。哪邊的樹高,就把那邊的樹向上旋轉。
- 所謂的左旋和右旋都是以子樹為原點的:如b是a的子樹,那麼旋轉就圍繞b來進行。
- 如果b是a的左子樹,那麼就圍繞b將a向右旋轉,看著就像是a直接掉下來了,掉成了b的右子樹。
- 如果b是a的右子樹,那麼就圍繞b將a向左旋轉,看著就像是a直接掉下來了,掉成了b的左子樹。
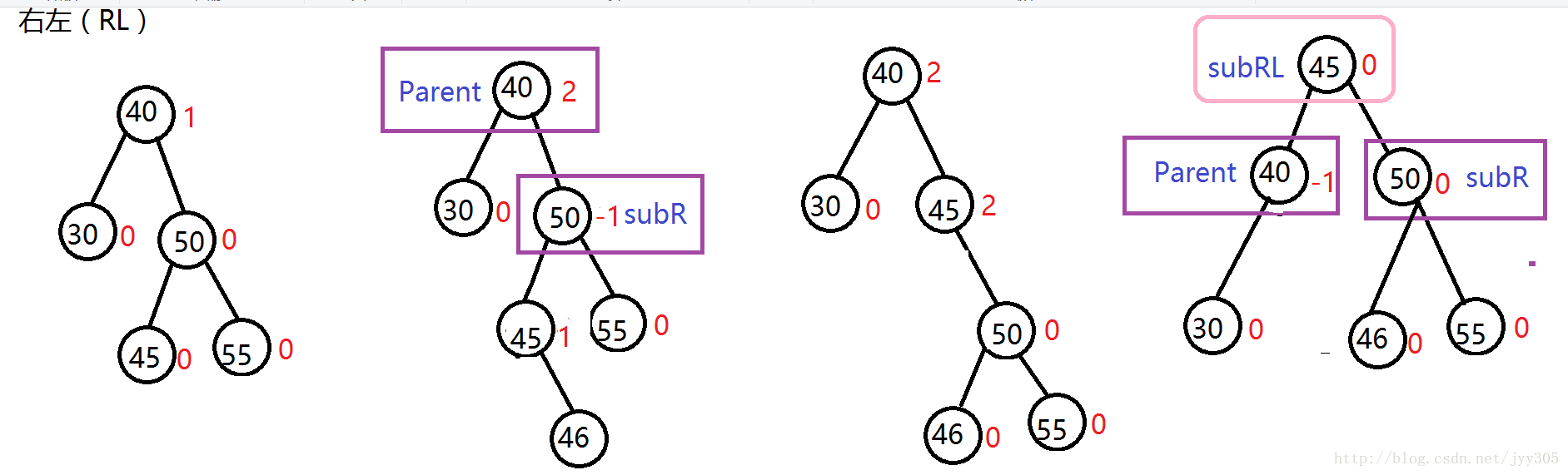
四種失衡情況
而在二叉樹中,任意結點孩子最多隻有左右兩個,而且導致失去平衡的必要條件就是當前結點的兩顆子樹的高度差等於2。因此,對於被破壞平衡的節點 a 來說致使失衡的插入操作有以下4中,其中左左和右右是隻需要一次旋轉,而左右和右左需要兩次旋轉。
| 插入方式 | 描述 | 旋轉方式 |
| LL | 在結點的左子樹的左子樹插入元素 | 右旋轉 |
| RR | 在結點的右子樹的右子樹插入元素 | 左旋轉 |
| LR | 在結點的左子樹的右子樹插入元素 | 先左旋後右旋 |
| RL | 在結點的右子樹的左子樹插入元素 | 先右旋後左旋 |
四種失衡情況的旋轉策略
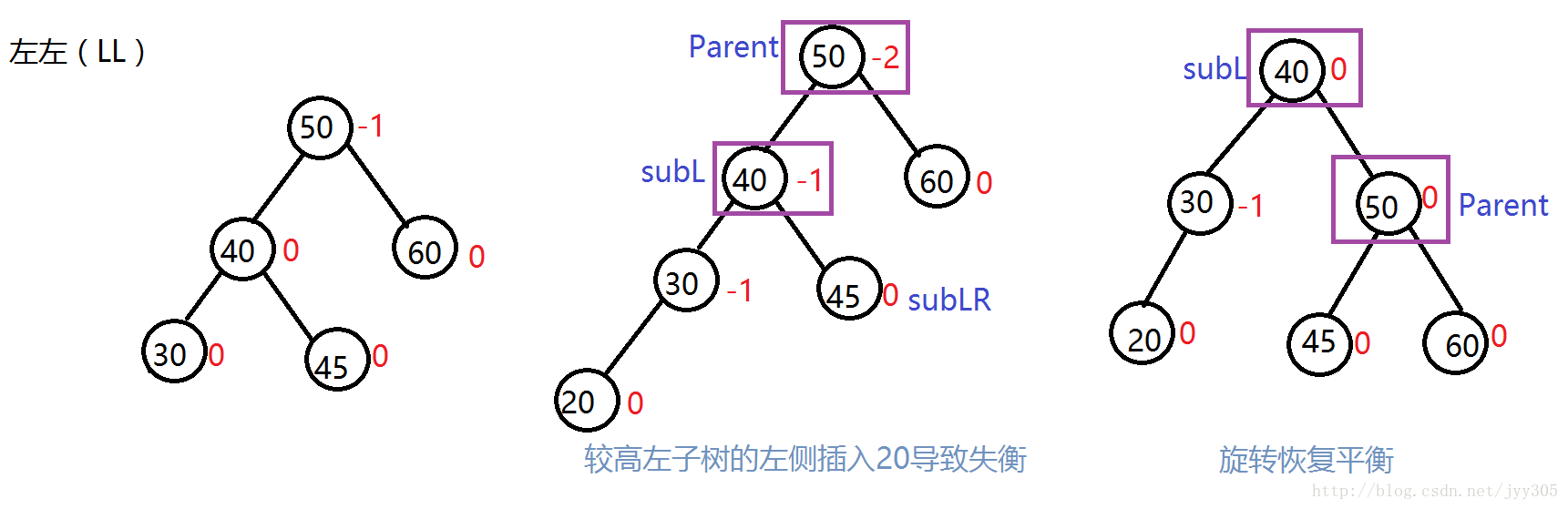
1. LL (左左) 模式 右旋轉
1-1左左模式和1-4右右模式只需要旋轉一次,其中旋轉的方式是一樣的,而旋轉方向不同而已,下面拿一個左左的模式:
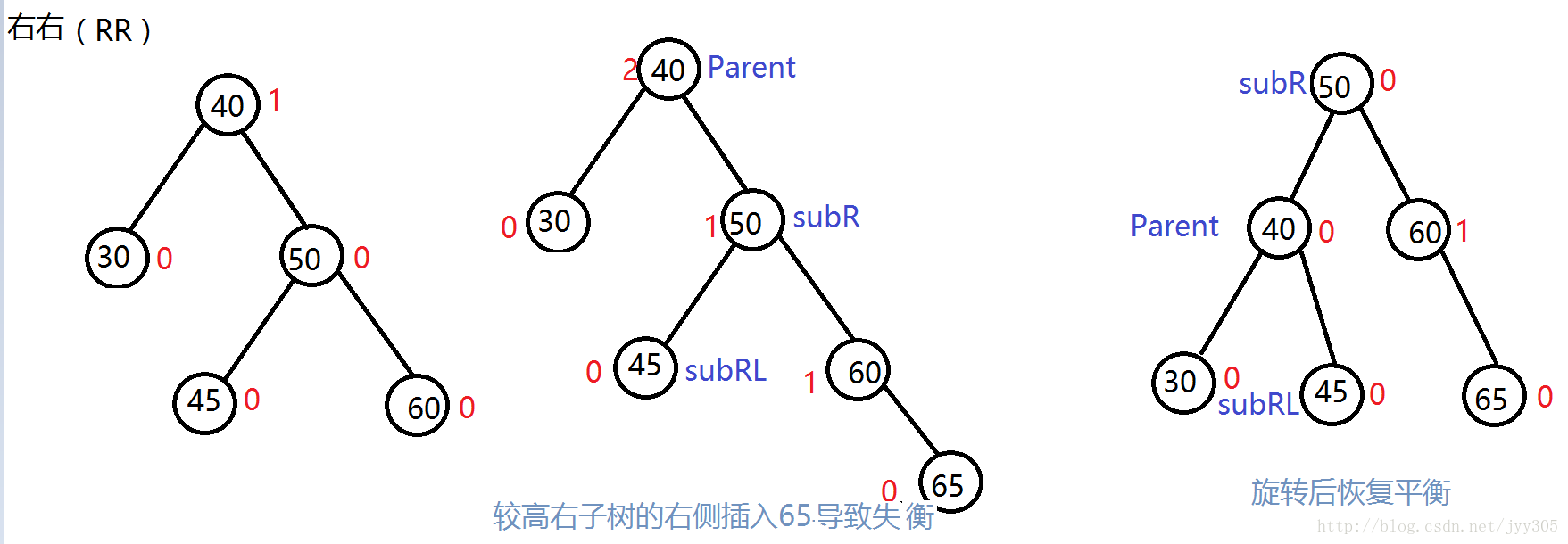
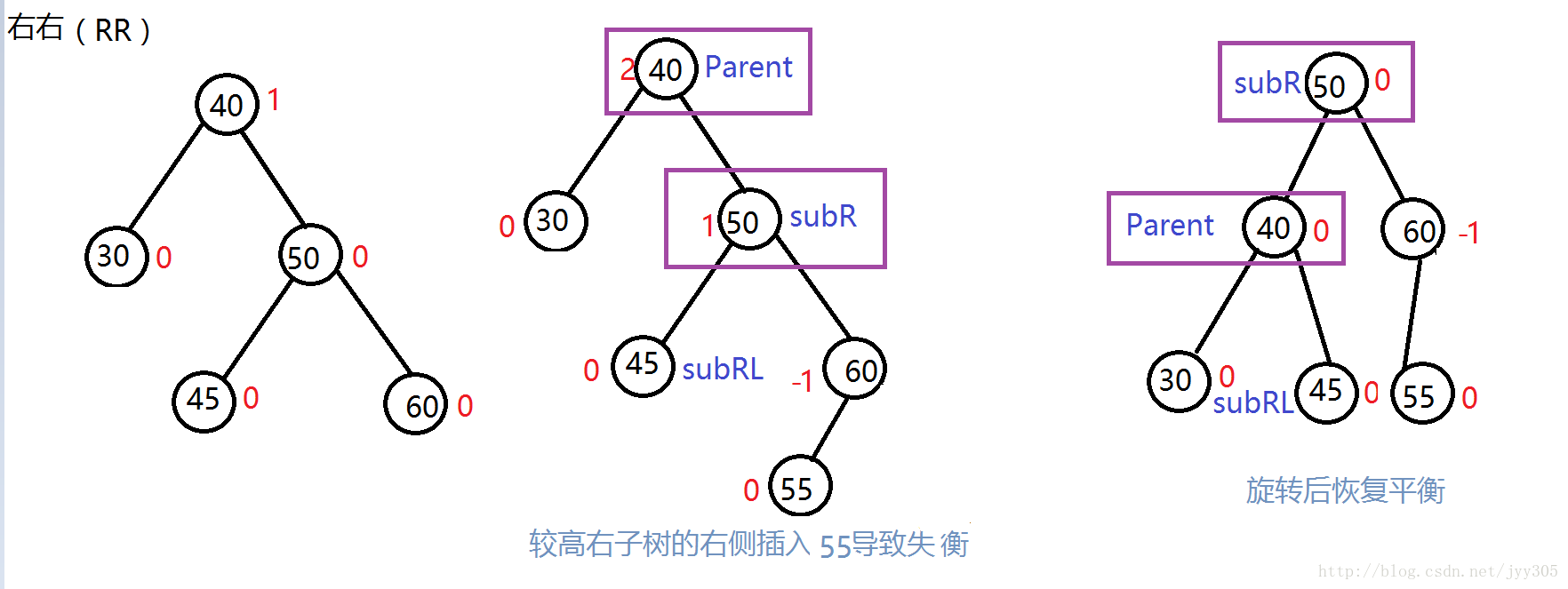
2. RR (右右) 模式 左旋轉
參考左左模式旋轉方式
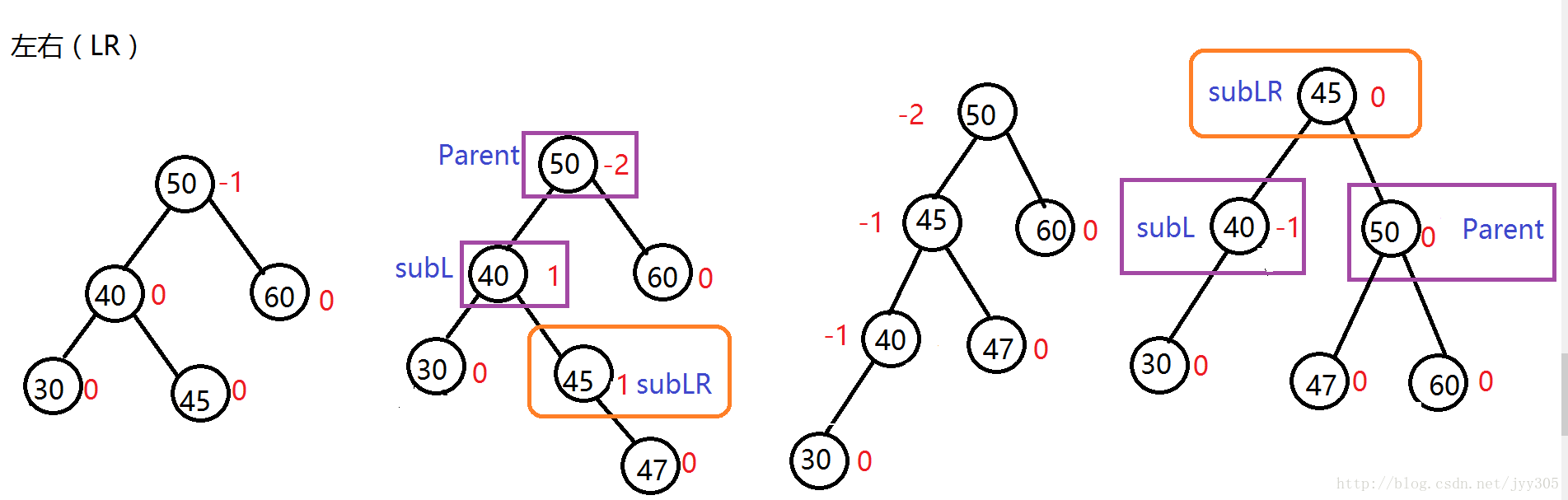
3. LR (左右) 模式
1-2左右和1-3右左都需要旋轉兩次,方向不一樣而已操作一樣,就拿1-2左右來說,如下圖所示:
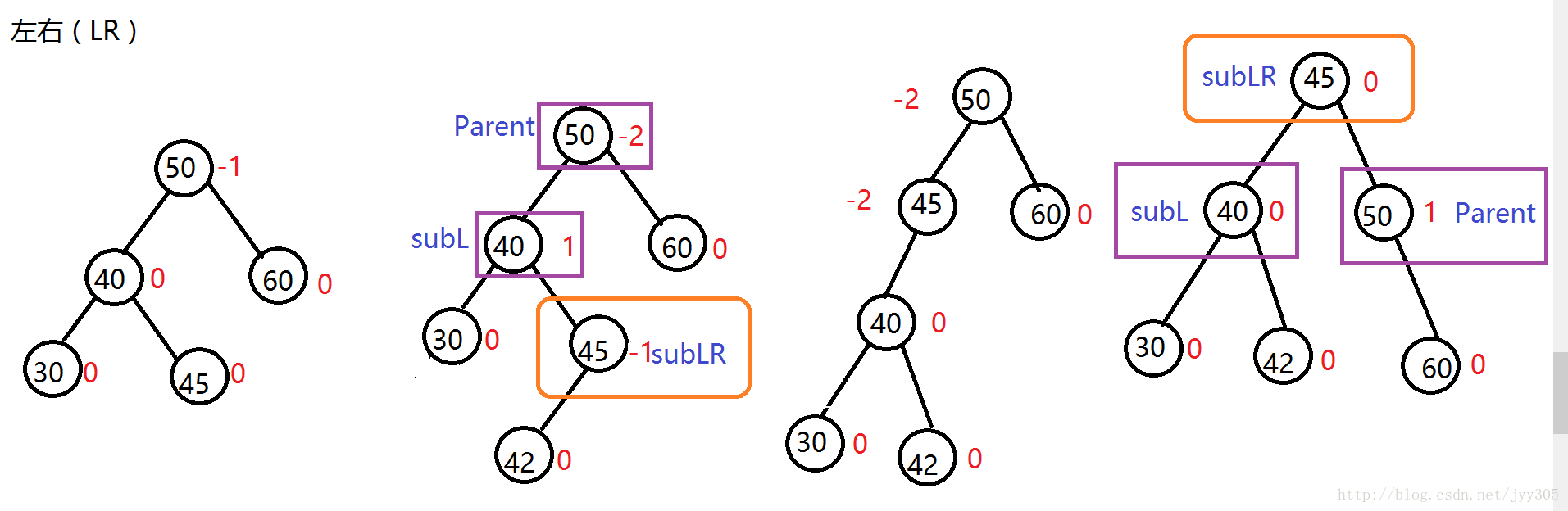
第二次旋轉:然後將這個第一次旋轉得到的左左模式二叉樹按照左左模式進行右旋即可,最終得到一個AVL樹。
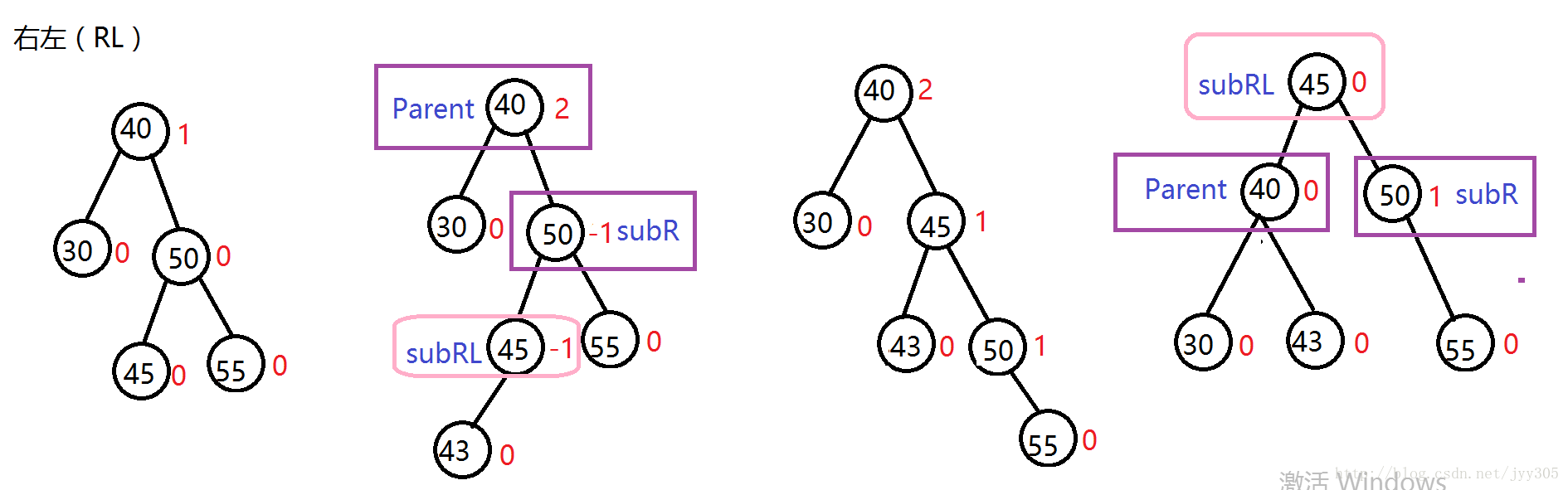
4. RL (右左) 模式
參考左右模式旋轉方式。
效能分析
平衡二叉樹的效能優勢:
很顯然,平衡二叉樹的優勢在於不會出現普通二叉查詢樹的最差情況。其查詢的時間複雜度為O(logN)。
平衡二叉樹的缺陷:
(1) 為了保證高度平衡,動態插入和刪除的代價也隨之增加。
(2) 所有二叉查詢樹結構的查詢代價都與樹高是緊密相關的,能否通過減少樹高來進一步降低查詢代價呢。我們可以通過多路查詢樹的結構來做到這一點。
(3) 在大資料量查詢環境下(比如說系統磁盤裡的檔案目錄,資料庫中的記錄查詢 等),所有的二叉查詢樹結構(BST、AVL、RBT)都不合適。
參考
參考圖片來源:https://blog.csdn.net/jyy305/article/details/70949010