暫無連結

新的家園

——過去已成為過去，而未來終將是過去。所有事物在出現的那一刻都註定成為歷史……

題目背景

公元 $8102$ 年，火星的生態環境遭到嚴重破壞，終於也難逃人類的掠奪，變成了一顆死星。

所有人，都乘坐飛船逃往了無盡的深空，除了你。

默默地，你步行在荒蕪的街道上，凝視著這片空無一人的大地——這個你由你親自見證創造，又親眼目送它毀滅的曾經人類的第二家園。

沙暴，四處是暗紅的赤鐵塵土捲起的沙暴。

紅色的煙塵之中，你望見了遠處廢棄的行星通道，往事如潮水般湧入腦海……

題目描述

你還記得行星通道系統有 $n$個站點， $E$條道路。這裡的道路同時包括了行星赤道上的行星通道和地面上的道路。每一條道路都是雙向通行的，且從任意一端通過第 $i$

最後一班飛船即將起航，所剩的時間不多了。你決定沿著行星通道上的站點移動，最後一次認真看看這個深紅的星球。

為了規劃路線，你需要知道一些站點之間移動耗費的最短時間。具體的來說，有 $q$個詢問。每一個詢問 $s_i,t_i$表示詢問從 $s_i$到 $t_i$的最短用時。 (注：上一題的條件在本題中不一定適用)

【輸入】

第一行三個整數 $n,E,q$，表示站點數，道路數量和詢問數。

接下來 $E$行每行三個整數 $u,v,w$表示 $u,v$間有一條雙向道路，通行時間為 $w$。

接下來 $q$行每行兩個整數 $s,t$，表示詢問 $s$站點到 $t$站點的最短用時。

【輸出】

一共有 $q$行輸出。

每一行一個整數，表示每一次詢問的答案。

【輸入樣例】

5 6 3
1 2 1
2 5 1
2 3 1
3 4 1
4 5 1
5 1 1
2 5
1 5
3 5

【輸出樣例】

1
1
2

【提示】

【資料範圍】

令 $m=E−n$

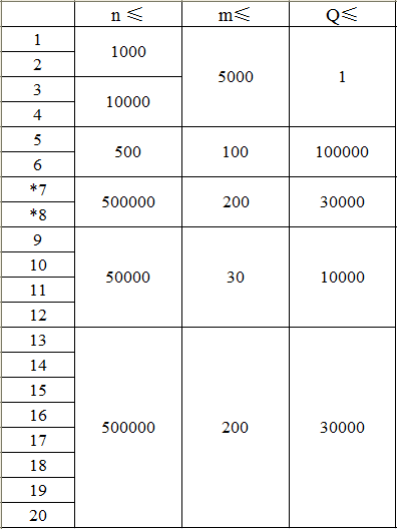
*：保證所有環以外的邊以 $(ai,bi)$形式依次給出，對於 $1≤i<n$，保證 $a_i<b_i$且 $b_i<a_i+1$。

保證 $0≤w≤1000$,答案在 $2^{31}−1$內。

題解

發現存在決策的節點只有通道的兩端，大環上的節點許多是沒有決策的，對於這些沒有決策的節點，我們可以把這些點變成一條邊，整張圖只保留是通道端點的點，這樣整張圖大小就是 $O(m)$的了。

詢問時，把起點終點加入圖中，跑一次最短路，得到答案後再把新加的邊刪掉，總複雜度為 $O(q\times 最短路(m,m))$。

程式碼

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int M=5e5+5;
struct sd{int to,w;}ed[M<<1];
bool operator<(sd a,sd b){return a.w>b.w;}
int loop[M],head[M],nxt[M<<1],dis[M],gra[M],le[M],ri[M],tot,n,m,q,cnt;
bool key[M],vis[M];
priority_queue<sd>dui;
void adde(int f,int t,int w){nxt[++cnt]=head[f],head[f]=cnt,ed[cnt]=(sd){t,w};}
void add(int u,int v,int w){adde(u,v,w),adde(v,u,w);}
void in()
{
	memset(loop,127,sizeof(loop));
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1,a,b,c;i<=m;++i)
	{
		scanf("%d%d%d",&a,&b,&c);
		if(a>b)swap(a,b);
		a==b-1?loop[a]=min(loop[a],c):(add(a,b,c),key[a]=key[b]=1);
	}
}
int dijkstra(int s,int t)
{
	for(int i=1;i<=tot;++i)dis[gra[i]]=inf,vis[gra[i]]=0;
	dui.push((sd){s,dis[s]=0});
	for(sd f;!dui.empty();)
	{
		f=dui.top(),dui.pop();
		if(vis[f.to])continue;
		vis[f.to]=1;
		for(int i=head[f.to];i;i=nxt[i])
		{
			if(!vis[ed[i].to]&&dis[ed[i].to]>dis[f.to]+ed[i].w)
			dis[ed[i].to]=dis[f.to]+ed[i].w,dui.push((sd){ed[i].to,dis[ed[i].to]});
		}
	}
	return dis[t];
}
void ac()
{
	for(int i=1,last=0;i<=n;++i)
	{
		loop[i]+=loop[i-1],le[i]=last;
		if(key[i]&&last)add(last,i,loop[i-1]-loop[last-1]);
		if(key[i])last=i,gra[++tot]=i;
	}
	for(int i=n,last=0;i;--i){ri[i]=last;if(key[i])last=i;}
	for(int i=1,s,t,x1,x2,x3,x4,x5,x6,pre=cnt;i<=q;++i)
	{
		scanf("%d%d",&s,&t);if(s>t)swap(s,t);
		if(s==t){puts("0");continue;}
		x1=head[le[s]],x2=head[s],x3=head[le[t]],x4=head[t],x5=head[ri[s]],x6=head[ri[t]];
		add(le[s],s,loop[s-1]-loop[le[s]-1]),add(s,ri[s],loop[ri[s]-1]-loop[s-1]);
		add(le[t],t,loop[t-1]-loop[le[t]-1]),add(t,ri[t],loop[ri[t]-1]-loop[t-1]);
		add(s,t,loop[t-1]-loop[s-1]);
		dis[s]=dis[t]=inf,vis[s]=vis[t]=0;
		printf("%d\n",dijkstra(s,t));
		cnt=pre,head[le[s]]=x1,head[s]=x2,head[le[t]]=x3,head[t]=x4,head[ri[s]]=x5,head[ri[t]]=x6;
	}
}
int main(){in();ac();}