暫無連結

玩

題目背景

你的昆特牌打的太好啦！不一會你就 $AK$ 了 $NOGP$

題面描述

你有一些矩形卡牌，每次你會作如下三個操作：
1.緊挨著最後一張牌往牌後面放一張牌，這張牌的底邊與 $X$ 軸重合且位於第一象限；（第一張牌最左邊位於 $X=$

輸入資料

第一行兩個數 $N、C$ 表示運算元、離線操作還是線上；
接下來 N 行每行是如下三種之一
$T=1$，接下來 $LEN、H$ 分別表示插入的牌的長、高；
$T=2$，接下來 $X$ 表示拿走哪一張牌，牌的編號按出現順序由小到大，從 $1$ 開始（不是操
作序號！），刪除的牌不會改變序號，若序號表示的牌已被刪除則不操作；
$T=3$，接下來 L、R 表示詢問區間；若詢問區間上沒牌，輸出 0。
若 $C=1$,則上面輸入中的 $LEN、H$（僅這兩項！）需要以下式子算出（ $lastans$ 為最近一次詢問答案，初值為 $0$）
$真實輸入 = (輸入*2333 + lastans*666 ) \%100000007+1; (1e8+7!)$

輸出資料

對每一個詢問操作輸出該段最高的位置高度是多少。

樣例資料

INPUT

6 0
1 5 3
1 8 2
3 2 6
1 2 4
2 2
3 2 6

OUTPUT

3
4

樣例解釋

注意拿走一張牌時要把後面的牌向前推；

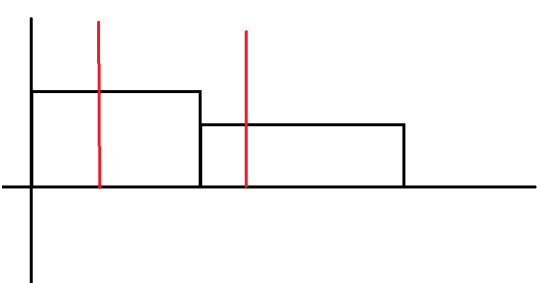
對於樣例前三次操作的影象
紅色線條表示詢問區間

資料範圍

對於 $40\%$的資料，沒有刪除操作；
對於額外 $20\%$的資料， $C=0$；
對於 $80\%$的資料， $N≤2*10^5$；
對於 $100\%$的資料， $N≤5*10^5$ ， $LEN、H≤10^9$， $L、R$ 不會超過 1e18 範圍，輸入的沒有負數。

TIPS

注意邊界情況！

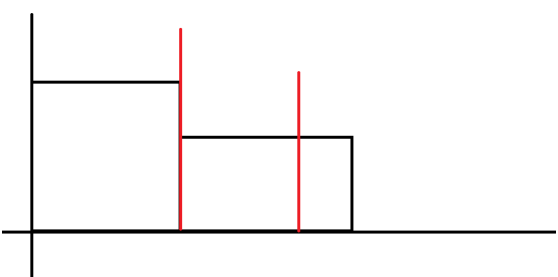
如這時最高點是左邊的牌的高度！
一個我看來沒什麼問題的問題的補充：若 $L=R$，答案不為 $0$ 哦
提前 $AK$ 的同學互相玩玩昆特牌吧！（霧）
強烈建議大家注意細節！

題解

很簡單的一道線段樹，以牌的標號建線段樹，維護長度和與最高的高度，查詢時線上段樹上二分座標所在牌的編號。

對於邊界問題，查詢的時候右邊界加一即可。

程式碼

#include<bits/stdc++.h>
#define ll long long
#define ls v<<1
#define rs ls|1
#define F(x) (x*2333+last*666)%100000007+1
using namespace std;
const int M=2e6+5;
int mx[M],tag[M],tot,n,typ;
ll sum[M],r;
char c;
ll read()
{
	for(r=0;!isdigit(c);c=getchar());
	for(;isdigit(c);c=getchar())r=(r<<1)+(r<<3)+c-'0';
	return r;
}
void out(int x)
{
	if(x>9)out(x/10);
	putchar(x%10+'0');
}
void up(int v)
{
	sum[v]=sum[ls]+sum[rs];
	mx[v]=max(mx[ls],mx[rs]);
}
void ins(int v,int le,int ri,int pos,int len,int h)
{
	if(le==ri){sum[v]=len,mx[v]=h;return;}
	int mid=le+ri>>1;
	if(pos<=mid)ins(ls,le,mid,pos,len,h);
	else ins(rs,mid+1,ri,pos,len,h);
	up(v);
}
void del(int v,int le,int ri,int pos)
{
	if(le==ri){sum[v]=mx[v]=0;return;}
	int mid=le+ri>>1;
	if(pos<=mid)del(ls,le,mid,pos);
	else del(rs,mid+1,ri,pos);
	up(v);
}
int get(int v,int le,int ri,ll pos)
{
	if(le==ri){return le;}
	int mid=le+ri>>1;
	if(sum[ls]>=pos)return get(ls,le,mid,pos);
	else return get(rs,mid+1,ri,pos-sum[ls]);
}
int ask(int v,int le,int ri,int lb,int rb)
{
	if(lb<=le&&ri<=rb){return mx[v];}
	int mid=le+ri>>1,ans=0;
	if(lb<=mid)ans=ask(ls,le,mid,lb,rb);
	if(mid<rb)ans=max(ans,ask(rs,mid+1,ri,lb,rb));
	return ans;
}
void in(){n=read(),typ=read();}
void ac()
{
	ll a,b,last=0;
	for(int i=1,op;i<=n;++i)
	{
		op=read(),a=read();
		if(op==1)
		{
			b=read();
			if(typ)a=F(a),b=F(b);
			ins(1,1,n,++tot,a,b);
		}
		else if(op==2)del(1,1,n,a);
		else
		{
			b=read();
			a=get(1,1,n,a),b=get(1,1,n,b+1);
			out(last=ask(1,1,n,a,b)),putchar(10);
		}
	}
}
int main(){in(),ac();}