[題解]TopCoder SRM 616 Div2 T3 TwoLLogo 18.8.12
2018.8.12 20:17
哎呀呀呀呀呀呀呀呀呀開心做了一個晚上終於把T3A掉了~\(≧▽≦)/~,如果沒有記錯大概是第一道完全獨立做的TCdiv2T3吧,哎呀呀呀呀越想越開心開心開心開心
原題
Problem Statement |
|||||||||||||
| Please note that this problem has a non-standard time limit: 3 seconds. A yet unknown "LL Company" wants to design a logo. After a long discussion, company designers decided that the logo should consist of two letters L drawn in some way. To start with something, designers drew N rows of M points each, one under another, so that these points form a rectangular grid. They also painted each point either white or black. Here is an example of what they could get for N = 4 and M = 5:  Designers agreed to draw each letter L as a union of a horizontal and a vertical line segment intersecting at their left and bottom ends, respectively. The segments must have positive lengths, and their endpoints must be white grid points. All grid points that lie on the segments must be white as well. For example, here are two valid placements of a letter: 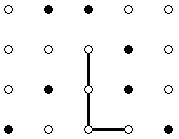 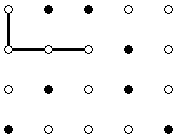 Note that neither the letters nor the grid can be rotated. The final requirement is that the two letters should be disjoint. That is, no white point should lie on two segments belonging to different letters. You are given the grid with N rows and M columns, encoded as a vector <string> grid Return the number of different possible logos with two L's drawn on them according to the requirements. Two logos are considered different if there is a pair of points that is connected by a line segment in exactly one of the logos. |
|||||||||||||
Definition |
|||||||||||||
|
|||||||||||||
Limits |
|||||||||||||
|
|||||||||||||
Constraints |
|||||||||||||
| - | grid will contain between 2 and 30 elements, inclusive. | ||||||||||||
| - | All elements of grid will contain the same number of characters. | ||||||||||||
| - | Each element of grid will contain between 2 and 30 characters, inclusive. | ||||||||||||
| - | Each character of grid will be either '.' or '#'. | ||||||||||||
Examples |
|||||||||||||
| 0) | |||||||||||||
|
|||||||||||||
| 1) | |||||||||||||
|
|||||||||||||
| 2) | |||||||||||||
|
|||||||||||||
| 3) | |||||||||||||
|
|||||||||||||
| 4) | |||||||||||||
|
|||||||||||||
| 5) | |||||||||||||
|
|||||||||||||
| 6) | |||||||||||||
|
|||||||||||||
| 7) | |||||||||||||
|
|||||||||||||
題目描述
有一個由黑點和白點構成的n*m的網格,可以把相鄰的白點連線起來。現在要通過連線這些白點得到兩個'L'字母,使得兩個字母互不相交,且端點也不能重合,求有多少種方案。
分析
仔細一想這一題好像還挺簡單的QWQ
Part 1
為了方便,記[(x1,y1) (x2,y2)]為以(x1,y1)和(x2,y2)為端點的線段
對於一個可以作為L的拐角處的點(i,j)
- 向上查詢第一個'#'出現的位置,記為(pos1,j),那麼,這一個'L'字母豎著的線段可以是
,一共有i-pos1-1種可能
- 向右查詢第一個'#'出現的位置,記為(i,pos2),那麼,這一個'L'字母橫著的線段可以是
,一共有pos2-j-1種可能
所以,以(i,j)點為轉折點放'L'字母的方案數就是
看了樣例之後,我們會發現,對於(i,j)我們不僅需要知道放字母的方案數,還需要知道從(i,j)出發,向上最多連up個點,向右最多連lf個點的方案數,所以我們可以與處理出:
f[i][j][up][lf]表示以(i,j)為轉折點,向上最多連up個點(不包括(i,j)),向右最多連lf個點(不包括(i,j))的方案數
Part 2
接著,因為資料範圍很小,所以我們把可以作為轉折點的點存下來,直接列舉兩個轉折點,算出方案數就可以啦
那麼,對於兩個點(ax,ay)和(bx,by),怎麼計算方案數呢?
我們先把轉折點排序,x小的在前,x相同時y大的在前,那麼有以下幾種情況
- ax=bx,這時分兩種情況
- 以(bx,by)為轉折點的字母向右最遠也不能到達(ax,ay)
那麼這時的方案數為f[ax][ay][up_a][lf_a]*f[bx][by][up_b][lf_b]
- 以(bx,by)為轉折點的字母向右可能會到達(ax,ay)——相交部分用紅色表示
這時,黑色字母向右最多隻能到達(ax,ay-1),所以方案數為f[ax][ay][up_a][lf_a]*f[bx][by][up_b][ay-by-1]
2.ax<bx
- 以(ax,ay)為轉折點的字母向右最遠也不能和另一個字母相交
- 或以(bx,by)為轉折點的字母向上最遠也不能和另一個字母相交
這兩種情況的方案都是f[ax][ay][up_a][lf_a]*f[bx][by][up_b][lf_b]
- 以(bx,by)為轉折點的字母向上可能會與另一個字母相交——相交部分用紅色表示
這時,我們要在兩個字母中選擇一個保留
- 如果選擇綠色,方案數為num1=f[ax][ay][up_a][lf_a]*f[bx][by][bx-ax-1][lf_b]
- 如果選擇黑色,方案數為num2=f[ax][ay][up_a][by-ay-1]*f[ax][ay][up_b][lf_b]
這種情況下的總方案數就是num1+num2減去兩種方案中重疊部分 f[ax][ay][up_a][by-ay-1]*f[bx][by][bx-ax-1][lf_b]
這樣,我們就可以開始敲程式碼了
程式碼
//tc is healthy, just do it
#include <bits/stdc++.h>
#define ll long long
using namespace std;
class TwoLLogo {
public:
long long countWays( vector <string> grid );
};
int n,m,cnt=0;
int a[35][35];
ll ans=0;
ll f[35][35][35][35];
void Init(){
for(int i=1;i<=30;i++)
for(int j=1;j<=30;j++)
a[i][j]=0;
for(int i=0;i<=30;i++)
for(int j=0;j<=30;j++)
for(int k=0;k<=30;k++)
for(int l=0;l<=30;l++)
f[i][j][k][l]=0;
ans=cnt=0;
}
struct nn{
int x,y,up,lf;
}q[1000];
int cmp(nn A,nn B){
if(A.x==B.x)return A.y>B.y;
return A.x<B.x;
}
void search(int x,int y){
cnt++;
q[cnt].x=x;q[cnt].y=y;
int up=0,lf=0;
int px,py;
px=x-1;
while(a[px][y]==0&&px>=1)up++,px--;
py=y+1;
while(a[x][py]==0&&py<=m)lf++,py++;
for(int i=1;i<=up;i++)
for(int j=1;j<=lf;j++)
f[x][y][i][j]=i*j;
q[cnt].up=up;q[cnt].lf=lf;
}
ll chk(int na,int nb){
int ax=q[na].x,ay=q[na].y,bx=q[nb].x,by=q[nb].y;
ll num=0;
if(ax==bx){
if(ay-by<=1)return 0;
if(ay>by+q[nb].lf){
return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][q[nb].lf];
}
return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][ay-by-1];
}
if(by>=ay){
if(by==ay){
if(bx-ax<=1)return 0;
if(bx>ax+q[nb].up)return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][q[nb].lf];
return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][bx-ax-1][q[nb].lf];
}
if(by>ay+q[na].lf)return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][q[nb].lf];
if(bx>ax+q[nb].up)return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][q[nb].lf];
num=f[ax][ay][q[na].up][q[na].lf]*f[bx][by][bx-ax-1][q[nb].lf];
if(by-ay>1){
num+=f[ax][ay][q[na].up][by-ay-1]*f[bx][by][q[nb].up][q[nb].lf];
num-=f[ax][ay][q[na].up][by-ay-1]*f[bx][by][bx-ax-1][q[nb].lf];
}
return num;
}
return f[ax][ay][q[na].up][q[na].lf]*f[bx][by][q[nb].up][q[nb].lf];
}
long long TwoLLogo::countWays(vector <string> grid) {
n=grid.size();m=grid[0].length();
Init();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(grid[i-1][j-1]=='.')a[i][j]=0;
else a[i][j]=1;
}
}
for(int i=2;i<=n;i++){
for(int j=1;j<=m-1;j++){
if(a[i][j]==0&&a[i-1][j]==0&&a[i][j+1]==0){
search(i,j);
}
}
}
ll num=0;
sort(q+1,q+cnt+1,cmp);
for(int i=1;i<=cnt;i++){
for(int j=i+1;j<=cnt;j++){
num=chk(i,j);
ans+=num;
}
}
return ans;
}
18.8.12 21:27