今天也才改出來一道題orz，大坑最近要填，，，

今天題目難度適中，暴力都打出來了，但是第二題“spfa死了”。

於是今天就改出來了第一題和去練了下dijkstra+堆優化。。。於是時間不夠用orz。。

---------------------------------------------------------------------------------------------------------------------------------------------------------------

首先我們看到這道題，很容易想到二分一個最大高度，然後列舉每個位置作為x所在地，找能把這個高度兩邊l，r把它圍起來的最大三角形，若所用積木少於m則加高這個最大高度，否則減少。

那麼找l，r的時間樸素暴力是O(n^2)的，肯定要T，於是考慮優化：

二分搭建的高度，最低為maxh+1，最高為maxh+sqrt(m)+1

如何在O(n)時間內check呢？

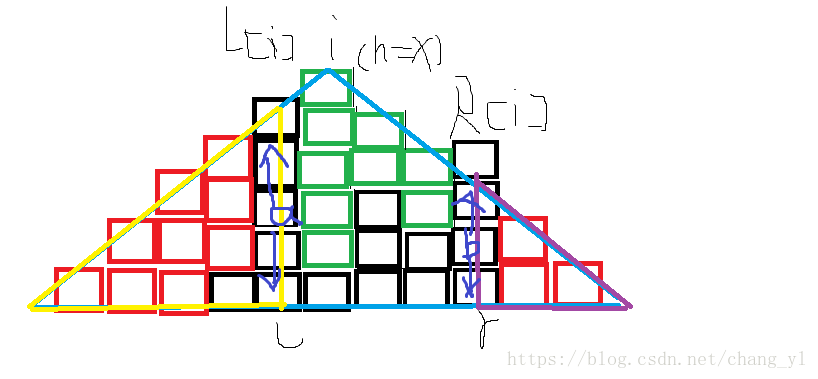
對於搭建積木，我們要搭出一個金字塔形，但是，並不是要搭建整個金字塔形，有時候只要搭建部分即可，如圖：

首先，要知道的是這道題相對每個i的l是遞增的。

我們發現，對於一個位置x，如果能找到它所對的l，那麼對於位置x-1，它的l必≤位置x所對的l，且從位置x所對的l ~x-1絕對不滿足能做綠色部分的左邊框。因為在向左移的過程中，左邊的每個位置的h的要求總是增大的（金字塔形）

所以l具有單調性。我們從n到1掃描每個位置

對r也是一樣，只要從左往右掃描即可。

我們僅需搭建綠色部分，而不需要搭建藍色方框內的整個金字塔

如何找到綠色部分呢？

設l為綠色部分的左邊界，r為綠色部分的右邊界，x為當前要搭建的金字塔頂，h為大金字塔塔高

我們需要在搭建的金字塔所需積木=整個大金字塔所需積木-黃色部分所需積木-紫色部分所需積木-棕色部分所需積木

設黃色部分高為a，則a=h-(x-l)（即圖中6-1=5），黃色部分所需積木為a*(a+1)/2。

同理，能算出紫色部分所需積木。

棕色部分所需積木=r前面所有已有積木-l前面所有已有積木。我們想到了什麼？字首和

這樣，綠色部分所需積木就算出來了，我們比較它與m的大小關係即可

程式碼實現：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pt putchar
#define ex pt('\n')
const int MAXN = 1e5 + 5;
int n,m;
int L[MAXN],R[MAXN];
ll h[MAXN],H[MAXN];
ll sum[MAXN];
ll ans = 0;
void in(int &x)
{
	int num = 0,f = 1; char ch = getchar();
	while(ch < '0' || ch > '9') {if(ch == '-') f = -1;ch = getchar();}
	while(ch >= '0' && ch <= '9') {num = (num<<3) + (num<<1) + (ch - '0'); ch = getchar();}
	x = num*f;
}
void lin(ll &x)
{
	ll num = 0,f = 1; char ch = getchar();
	while(ch < '0' || ch > '9') {if(ch == '-') f = -1;ch = getchar();}
	while(ch >= '0' && ch <= '9') {num = (num<<3) + (num<<1) + (ch - '0'); ch = getchar();}
	x = num*f;
}
void out(int x)
{
	if(x < 0) x = -x,pt('-');
	if(x > 9) out(x/10);
	pt(x%10 + '0');
}

inline void init()
{
	in(n); in(m);
	for(int i = 1;i <= n;i++)
	{
		lin(h[i]); sum[i] = sum[i-1] + h[i];
		ans = max(ans,h[i]);
	}
}

bool check(ll x)
{
	int l = n,r = 1;
	for(int i = n;i >= 1;i--) {while(h[l] < x-(i-l) && l >= 1) l--;L[i] = l;}
	for(int i = 1;i <= n;i++) {while(h[r] < x-(r-i) && r <= n) r++;R[i] = r;}
	for(int i = 1;i <= n;i++)
	{
		if(R[i] == n+1 || L[i] == 0) continue;
		ll a = x - (i - L[i]),b = x - (R[i] - i);
		ll s = x * x - (b + 1) * b/2ll - (a + 1) * a/2ll;
		if(s - (sum[R[i] - 1] - sum[L[i]]) <= m) return 1;
	}
	return false;
}

inline void work()
{
	ll l = ans + 1,r = (ll)(sqrt(m) + 1.00) + ans + 1; 
	while(l < r)
	{
		ll mid = (l + r) >> 1;
		if(check(mid)) l = mid+1;
		else r = mid;
	}
	out(l-1);
}

int main()
{
//	freopen("block.in","r",stdin);
//	freopen("block.out","w",stdout);
	init();
	work();
	return 0;
}