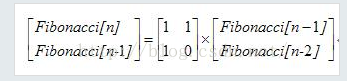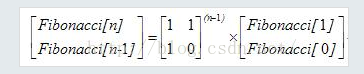Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 19397		Accepted: 13420

Description

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n

≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

如：在斐波那契數列之中

f[i] = 1*f[i-1]+1*f[i-2]  f[i-1] = 1*f[i-1] + 0*f[i-2];

即

所以

就這兩幅圖完美詮釋了斐波那契數列如何用矩陣來實現。

//POJ3070
//快速矩陣冪演算法 
//fibonacci 由於給出的n特別大，所有常用的遍及行不通，
//通過推導矩陣冪的方程進而更方便實現 ，在mul_mat中注意要求模資料太大了 
#include "iostream"
#include "algorithm"
#include "cstdio"
#include"cstring"
#define rep(i,j,k) for(int i=j;i<=k;i++)
const int mod=1e4;
typedef long long LL;
using namespace std;
struct mat
{
	LL a[2][2];
};//記得加引號 
mat mul_mat(mat &a,mat &b)
{
	mat res;
	memset(res.a,0,sizeof(res.a)); 
	rep(i,0,1)
		rep(j,0,1)
			rep(k,0,1)
			{
				res.a[i][j]=res.a[i][j]+a.a[i][k]*b.a[k][j]%mod;
			}
	return res;
}
void pow_mat(int n)
{
	mat res,a;
	a.a[0][0]=a.a[0][1]=a.a[1][0]=1;
	a.a[1][1]=0;
	//注意儘管結構體是在全域性定義的，但是不論是陣列還是int都不會被初始化為0
	memset(res.a,0,sizeof(res.a)); 
	res.a[0][0]=1,res.a[1][1]=1;
	//初始化完畢 
	while(n)
	{
		if(n&1) res=mul_mat(a,res);//試過了，在矩陣中對於單位矩陣，換下位置沒關係
		a=mul_mat(a,a);//如mul_mat(res,a);
		n>>=1;
	}
	cout<<res.a[0][0]%mod<<endl;
}
int main()
{
	int n;
	while(cin>>n&&n!=-1)
	{
		if(n==0)
		{
			cout<<"0"<<endl;
			continue;
		}
		pow_mat(n-1);
	}
	
	return 0;
}

 注意：大數，結構體後面的引號，結構體要初始化裡面的值

演算法必須得寫，看懂了遠遠不夠，這些權當筆記

that's all