通過詳解,認識遞迴(recursion)
首先先對遞迴進行入門。
遞迴是以自相似的方式重複專案的過程。在程式語言中,如果程式允許您在同一函式內呼叫函式,則稱其為函式的遞迴呼叫。
簡而言之,遞迴就是函式的自身呼叫。可以看看下面的遞迴使用:
void Recursive() { Recursive();//call itself } int main(void) { Recursive(); system("PAUSE"); return 0; }
借前輩一句話,遞迴定義就是:遞迴中的“遞”就是入棧,遞進;“歸”就是出棧,迴歸。
因為遞迴在整個函式結束時才釋放資料區,而每一次呼叫函式都會儲存臨時的變數,因此遞迴次數過多,會造成棧溢位,上面的例子就會出現這種狀況。
如果你會將遞迴與return聯絡起來,但實際上return的作用只是將值返回給呼叫引數的函式。
N項求和
我們以前都計算過求1+2+3+4+...+n,n項求和。現在要求我們使用遞迴寫出來。
1.我們設第n項的和為sum(n),而前n項之和,可以由前n-1項之和加第n項。用表示式就是:sum(n-1) + n。
可以得到關係式:sum(n) = sum(n -1) + n;
2.接下來我們可以想一下,sum(n-1)又等於前一項加n-1一直迴圈下去計算,直到sum(2) = sum(1) + 2;計算完畢,此時sum(2)是我們要求的值,sum(1)是未知的,因此我們還需要知道sum(1)
由1, 2的敘述,我們列出:
sum(n) = sum(n-1) + n; sum(1) = 1;
我們將第一個式子稱作為“關係”, 第二個式子稱作“出口”(可以理解為結束遞迴的條件)。
由此我們可以寫出程式:
#include <stdio.h> #include <stdlib.h> int sum(int n) { if (n == 1) { return 1; } else { return sum(n - 1) + n; } }int main(void) { int k = sum(100); printf("%d\n", k); system("PAUSE"); return 0; }
Question:
接著我們可以試著自己做一下n!的遞迴計算,同樣是第n項等於 前n-1項相乘 * 第n項,出口為第1項,當然出口也可以為第m項(m>0&&m<=n),但我們這裡算n!,就不管了。
奇/偶數求和
同樣,對於奇數,偶數求和也就是前n項的變型,這裡不再說,我們這裡可以對奇/偶數求第n項的值,進行遞迴計算。這裡舉例奇數計算:1+3+5+7...,設num(n)為第n個奇數。
1.通過第一個例子我們首先可以列出關係,num(n) = num(n - 1) + 2;
2.寫出出口,num(1) = 1;
寫出主要程式:
int num(int n) { if (n == 1) { return 1; } else { return num(n - 1) + 2; } }
斐波那契數列(Fibonacci sequence)
接著我們看看 斐波那契數列:1, 1, 2, 3, 5, 8, 13...
得出規律,後一項等於前兩項相加。寫出關係式f(n) = f(n-1) + f(n-2);
隨之我們對關係式的出口(結束條件)進行判斷,我們需要求f(n),而f(n-1)和f(n-2)都是未知的,我們只寫其中一項為出口都是不夠的,因此我們需要兩個出口。f(1) = 1; f(2) = 1;
通過關係和出口,我們寫出:
f(n) = f(n-1) + f(n-2); f(1) = 1; f(2) = 1;
寫出程式:
#include <stdio.h> #include <stdlib.h> int f(int n) { if (n == 1) return 1; if (n == 2) return 1; return f(n - 1) + f(n - 2); } int main(void) { int k = f(7); printf("%d\n", k); system("PAUSE"); return 0; }
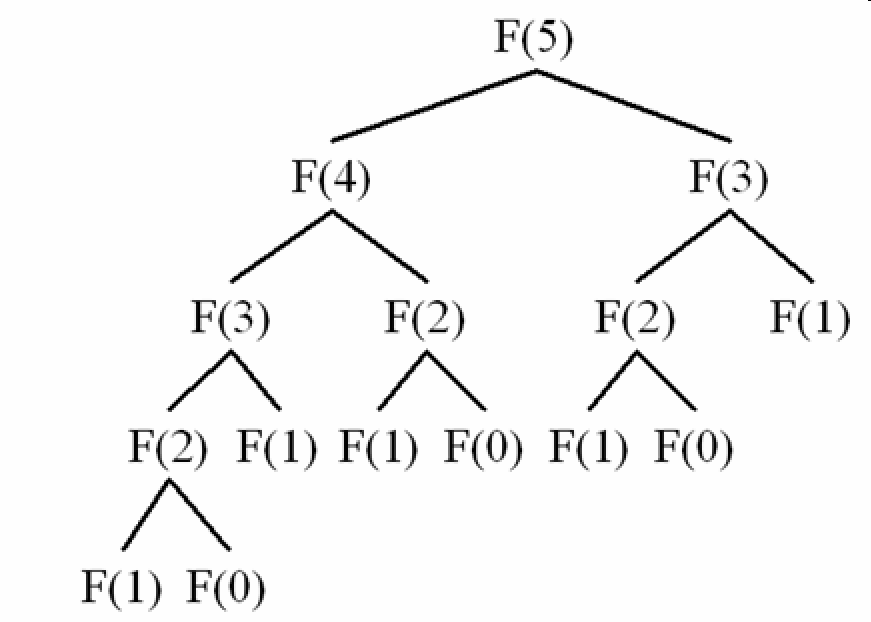
可以發現越高層的函式呼叫,自身呼叫的次數越多。
陣列求和
使用遞迴,對陣列array[] = { 1, 2, 3, 4, 5, 6};求和。
和之前n項求和思想相似,不過這裡多了將陣列地址傳入,同樣我們可以將陣列關係寫出 sum(array, n) = sum(array, n-1) + array[n]; 注意:我們這裡傳入的n應當是陣列的最大下標(陣列從0~n-1,n個數)。
很顯然作為遞迴出口的應當是當陣列下標為0時,sum(array, 0) = array[0];
我們可以寫出程式:
#include <stdio.h> #include <stdlib.h> int sum(int *arr, int n) { if (n == 0) return arr[0]; return sum(arr, n - 1) + arr[n]; } int main(void) { int array[] = { 1, 2, 3, 4, 5, 6 }; int k = sum(array, sizeof(array) / sizeof(int) - 1);//這裡填陣列最大下標 //int k = sum(array, 5); printf("陣列元素之和:%d", k); system("PAUSE"); return 0; }
漢諾塔問題
有三根杆子A,B,C。A杆上有N個(N>1)穿孔圓環,盤的尺寸由下到上依次變小。要求按下列規則將所有圓盤移至C杆:
- 每次只能移動一個圓盤;
- 大盤不能疊在小盤上面。
這道題的解題步驟就三個:
- 將A(source)杆中前n - 1個盤移到B(auxiliary)杆;
- 將A(source)杆最後一個盤移到C(destination)杆;
- 將B(auxiliary)杆n - 1個盤移到C(destination)杆;
動態圖演示(借前輩圖一用)

如果這樣說你還是不能理解過程,那麼我們就回想一下之前的n項求和,我們將前n-1項 + 第n項。那麼在這裡,我們將前n-1個盤看成一個整體(盤的位置不變),將最後一個大盤看成一個整體,先將那一大坨移到B杆,再把A杆剩下的那個大盤移到C杆,然後我們再把那一大坨移到C杆。
(此地插圖)
整體過程:
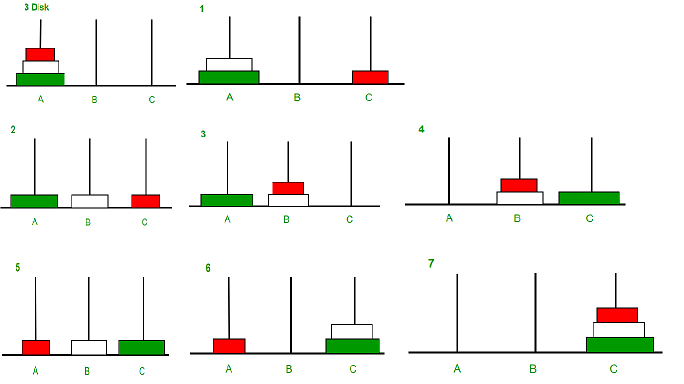
a.同樣的這道題我們通過解題步驟去找關係式:(整個函式的宣告是void Hanoi(int n, char SourcePole, char AuxiliaryPole, char DestinationPole);)
- Hanoi(n - 1, SourcePole, DestinationPole, AuxiliaryPole);
- printf("將盤%d,從%c柱------>%c柱\n", n ,SourcePole, DestinationPole);
- Hanoi(n - 1, AuxiliaryPole, SourcePole, DestinationPole);
(因為輸出物件是SourcePole到DestinationPole,因此我們要將A杆的盤轉移到B杆上,就需要在遞迴呼叫函式,傳入引數時,將引數換位。)
b.接著我們寫出口,移動n - 1個盤,也就是1~(n -1),當n = 0時結束函式。
因此寫出程式:
#include <stdio.h> #include <stdlib.h> void Hanoi(int n, char SourcePole, char AuxiliaryPole, char DestinationPole){ if(n == 0){ return; } Hanoi(n - 1, SourcePole, DestinationPole, AuxiliaryPole); printf("將盤%d,從%c柱------>%c柱\n", n ,SourcePole, DestinationPole); Hanoi(n - 1, AuxiliaryPole, SourcePole, DestinationPole); } int main(void) { Hanoi(3, 'A', 'B', 'C'); system("PAUSE"); return 0; }
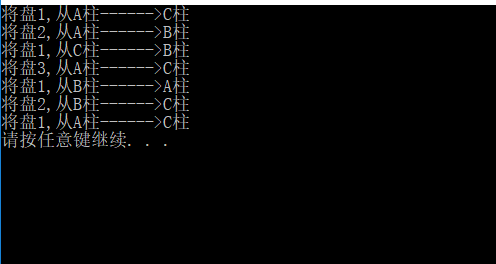
當然,對於出口也有另一種,盤數是從1~(n-1)的,當n = 0時結束入棧,當n = 1時恰好是最後一個入棧的。因此,可以當n = 1時進行一次移盤操作之後結束入棧。
此時的程式碼為(將SourcePole...更換變數名,便於讀者閱讀):
#include <stdio.h> #include <stdlib.h> void Hanoi(int n, char A, char B, char C){ if(n == 1){ return printf("將盤%d,從%c柱------>%c柱\n", n ,A, C); } Hanoi(n - 1, A, C, B); printf("將盤%d,從%c柱------>%c柱\n", n ,A, C); Hanoi(n - 1, B, A, C); } int main(void) { Hanoi(3, 'A', 'B', 'C'); system("PAUSE"); return 0; }
還有一道從N個球中取M個球的遞迴問題也不錯,有興趣可以看:點選連結
可以看看這個,繞一下入棧出棧,理解遞迴的執行。(PS:等會起來解析)
#include <stdio.h> #include <stdlib.h> void func(int num) { while(num>1) { //func(num-1); printf("%c",65+num-1); printf("%c",65); func(--num); } } int main(void) { int num; scanf("%d",&num); func(num); return 0; } /* --num CABABA --num變成2進行遞迴,同時,進入迴圈進行判斷,所以列印兩次2的值,然後,都變為1,再次分別進入迴圈與遞迴,不滿足 退出 num-- CACA... 首先num進入,分別進入迴圈和遞迴,在遞迴中,num自減1,等待本次遞迴結束,因為num=3時恆大於1,所以遞迴一直未結束,造成死迴圈。 num-1 CABABAB...首先,num-1,變成2,2進入,迴圈,遞迴,變成,1,遞迴不滿足,退出本次遞迴,回到上次遞迴,變成2,2進入迴圈,遞迴,變成1... 前: --num AABAAA num-- 崩潰 num-1 BABA...*/
各位讀者能夠有收穫便是我最大的快樂!寫教程不易,熬夜傷身,有個贊什麼的,我也是不介意滴!哈哈哈!
