【劍指offor】1、二維陣列中的查詢
阿新 • • 發佈:2018-11-07
題目連結:
二維陣列中的查詢
題目描述:
在一個二維陣列中(每個一維陣列的長度相同),每一行都按照從左到右遞增的順序排序,每一列都按照從上到下遞增的順序排序。請完成一個函式,輸入這樣的一個二維陣列和一個整數,判斷陣列中是否含有該整數。
解題思路
兩種思路
方法1
把每一行看成有序遞增的陣列,利用二分查詢,通過遍歷每一行得到答案。時間複雜度是nlogn
java程式碼:
public class Solution {
public boolean Find(int target,int [][] array) {
for C++程式碼:
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
if(array.size()<1)return false;
int low,high,mid;
int 方法2
利用二維陣列由上到下,由左到右遞增的規律,如下圖:
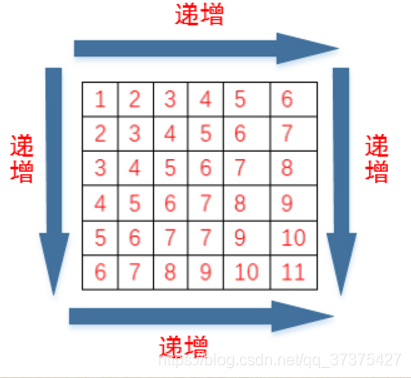
那麼選取右上角或者左下角的元素a[row][col]與target進行比較,當target小於元素a[row][col]時,那麼target必定在元素a[row][col]所在行的左邊,不可能在下面,因為下面的元素比a[row][col]大。即col–;
當target大於元素a[row][col]時,那麼target必定在元素a[row][col]所在列的下邊,不可能在左邊,因為邊面的元素比a[row][col]小。即row++;
java程式碼:
public class Solution {
public boolean Find(int target, int [][] array) {
if(array.length<1)return false;
int row=0,col=array[0].length-1;
while(row<array.length && col>=0){
if(target == array[row][col])return true;
else if(target>array[row][col])++row;
else --col;
}
return false;
}
}
C++程式碼:
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
if(array.size()<1)return false;
int row=0,col=array[0].size()-1;
while(row<array.size() && col>=0){
if(target==array[row][col])return true;
else if(target>array[row][col]) ++row;
else --col;
}
return false;
}
};
總結
方法一很簡單,但是效率不高。方法二比較巧妙,利用了該題中陣列的特性,實際上可以將方法二想象成二維空間的二分搜尋。它還是一種二分法的應用。
學習探討加:
qq:1126137994
微信:liu1126137994
